Ol — V2X 35 страница

J \ In [cj* + с₂ (©? + со!)] da, d(D_a, о

где с_х, с₂—постоянные. Произведя интегрирование, найдем окон­чательно, что вблизи точки перехода термодинамический потен­циал имеет вид

фъа-I Ь(Т-Т_с)Чп\Т-Т_с\, (151,13)

^а) В рассматриваемой модели температура влияет только на упорядочен­ность ориентации диполей, но не на расстояния между ними («коэффициент теплового расширения» решетки равен нулю). В таком случае безразлично, говорить ли о свободной энергии или о термодинамическом потенциале.

где a, b—снова постоянные (причем Ь >0). Сам потенциал не­прерывен в точке перехода, а теплоемкость обращается в беско­нечность по закону

СтЬЫ\Т — Т_е\, (151,14)

симметричному по обе стороны точки перехода.

Роль параметра порядка ц в рассмотренной модели играет средний дипольный момент в узле (спонтанная поляризация решетки), отличный от нуля ниже точки перехода и равный нулю выше ее. Температурная зависимость этой величины тоже может быть определена; вблизи точки перехода параметр по­рядка стремится к нулю по закону

л =const(r_c—7')^|/8 (151,15)

(L. Onsager, 1947) ^[46]).

Корреляционная функция определяется как среднее значение произведения флуктуации дипольного момента в двух узлах решетки. Корреляционный радиус оказывается стремящимся к бесконечности при Т—>Т_е по закону 1/\Т — Т_с\, а в самой точке Т = Т_С корреляционная функция убывает с расстоянием по закону

< Ae_klДа_и„ > со [(* -m)^[47] + (I-п)*]- >/в.

Эти результаты, а также результаты решения задачи о свойствах той же модели во внешнем поле показывают, что ее поведение вблизи точки фазозого перехода удовлетворяет требованиям гипотезы о масштабной инвариантности. При этом критические индексы имеют следующие значения:

а = 0, 6 = 1/8, 7 = 7/4, 6 = 15, е = 0,

р=8/15, v = l, £ = 1/4 ^(151,1Ь)

(индекс £ определен согласно (148,7) с d=2)^[48]).

§ 152. Ван-дер-ваальсова теория критической точки

В § 83 уже было отмечено, что критическая точка фазовых переходов между жидкостью и газом является особой точкой для термодинамических функций вещества. Физическая природа этой особенности подобна природе особенности в точках фазо­вого перехода второго рода: подобно тому, как в последнем случае она связана с возрастанием флуктуации параметра по­рядка, так при приближении к критической точке возрастают флуктуации плотности вещества. Эта аналогия в физической природе приводит также и к определенной аналогии в возмож­ном математическом описании обоих явлений, о чем будет идти речь в следующем параграфе.

Предварительно, однако, в качестве необходимой предпосылки рассмотрим описание критических явлений, основанное на пре­небрежении флуктуациями. В такой теории (аналогичной при­ближению Ландау в теории фазовых переходов второго рода) термодинамические величины вещества (как функции перемен­ных V и Т) предполагаются не имеющими особенности, т. е. могут быть разложены в степенные ряды по малым изменениям этих переменных. Все дальнейшие излагаемые в этом параграфе результаты являются поэтому следствием лишь обращения в нуль производной (dP/dV)r

Прежде всего выясним условия устойчивости вещества при

U)_r-0. (152,1)

При выводе термодинамических неравенств в § 21 мы исходили из условия (21,1), из которого было получено неравенство (21,2), выполняющееся при условиях (21,3—4). Интересующему нас те­перь случаю (152,1) соответствует особый случай условий экстре­мума, когда в (21,4) стоит знак равенства:

Квадратичная форма (21,2) может быть теперь, в зависимости от значений SS и 6V, как положительной, так и равной нулю; поэтому вопрос о том, имеет ли величина Е—ToS-\-P₀V минимум, требует дальнейшего исследования.

Мы должны, очевидно, исследовать именно тот случай, когда в (21,2) стоит знак равенства:

^(6S)»+2^eS6V-f§^(6V)«=0. (152,3)

Принимая во внимание (152,1), это равенство можно переписать следующим образом:

(S⁶⁵+^bv)²- -иг [^б ж]²=£ =о-

<3²£ _

dS [49] dS

Таким образом, равенство (152,3) означает, что мы должны рассматривать отклонения от равновесия при постоянной темпе­ратуре (6Г = 0).

При постоянной температуре исходное неравенство (21,1) принимает вид: 8F + P6V>0. Разлагая 8F в ряд по степеням

d²F /дР\

6V и учитывая, что предполагается — (^pL^^0, находим

Для того чтобы это неравенство было справедливо при любом 6V, должно быть!)

{Ш)т=⁰' {m)r<°- <¹⁵²'⁴)

Обратимся теперь к исследованию уравнения состояния ве­щества вблизи критической точки. При этом вместо переменных Т и V будет удобнее пользоваться переменными Тип, где п — плотность числа частиц (число частиц в единице объема). Введем также обозначения

t=T-T_KV, р = Р—Р_кр, г| = п-п_кр. (152,5)

В этих переменных условия (152,1) и (152,4) записываются как

В=°- №),><> (152,6)

Ограничиваясь первыми членами разложения по малым t и т), напишем зависимость давления от температуры и плотности в виде

p = W+2arr] + 4£r|^s (152,7)

с постоянными а, Ь, В. Членов ~ т) и ~ и² в этом разложе­нии нет в силу первых двух из условий (152,6), а в силу третьего В > 0. При t > 0 все состояния однородного тела устойчивы (разделения на фазы нигде не происходит), т. е. должно быть (dp/dr\)_t > 0 при всех и; отсюда следует, что а > 0. Членов раз­ложения ~ trf и ~ t²r\ можно не выписывать, как заведомо малых по сравнению с членом ~ tr\; сам же член tv должен быть оставлен, поскольку он входит в необходимую ниже

производную

др\

о>| It

-2at + 125п^[50].

(152,8)

Выражение (152,7) определяет изотермы однородного вещества вблизи критической точки (рис. 73). Эти изотермы имеют вид, аналогичный ван-дер-ваальсовым (рис. 19). При t < 0 они про­ходят через минимум и максимум, а равновесному переходу жидкости в газ отвечает горизонтальный отрезок (AD на нижней

изотерме), проведенный согласно условию (84,2). Понимая в этом условии под V молекулярный объем

п

п

⁷ - ^{1 1} (152,9)

v--

кр

запишем его в виде

D г)г

jnd/7 = jr,(|2.)₍dr) = 0. (152,10)

А л,

После подстановки (152,8) это
Рис. 73. условие приводит к следующим

значениям плотности двух нахо­дящихся в равновесии друг с другом фаз:

Лх = -ч,= Уж-' <¹⁵²'^П)

Плотности же ц[ и г)₂, соответствующие границам метаста­бильных областей (точки В и С на рис. 73) определяются условием (dp/dx\)_t = 0, откуда находим¹)

6В ■

(152,12)

Подстановка (152,11) обращает сумму двух последних членов в (152,7) в нуль. Поэтому

p = bt (t<0) (152,13)

есть уравнение кривой равновесия жидкости и пара в плоскости р, t (и поэтому b > 0)^[51]). Согласно уравнению Клапейрона — Клаузиуса (82,2) вблизи критической точки теплота испарения

^х) В теории, учитывающей особенности термодинамических величин на границе метастабильных состояний, никакой кривой ВС вообще нет.

q^bT^-^-. (152,14)

Из (152,11) следует поэтому, что при t—*0 эта теплота стре­мится к нулю по закону

q^V~t. (152,15)

Из формулы (16,10) следует, что в критической точке, вместе с обращением в нуль (dp/dr\)_t, обращается в бесконечность те­плоемкость С_р. С учетом (152,8) найдем, что

^^aT+W' ^(152Л6)

В частности, для состояний на кривой равновесия имеем т) с/э V—t, и потому С_рсл(— t)' ^[52] .

Наконец, рассмотрим в рамках излагаемой теории флуктуа­ции плотности вблизи критической точки. Необходимые для этого общие формулы были уже получены в § 116, а для их применения надо лишь установить конкретный вид величины AF_n—изменения полной свободной энергии тела при его откло­нении от равновесия.

Представим AF_a в виде

AF_a=l(F-F)dV,

где F—свободная энергия, отнесенная к единице объема, a F — ее среднее значение, постоянное вдоль тела. Разложим F—F по степеням флуктуации плотности Ап = п—п (или, что то же, Дг) = г) — г|) при постоянной температуре. Первый член разло­жения пропорционален An и при интегрировании по объему обращается в нуль в силу неизменности полного числа частиц в теле. Член второго порядка^[53]):

\дп²)т \дп)т п \дп)т (поскольку при r = const: dp, = odP, где v= Цп—молекулярный объем).

Наряду с этим членом, обращающимся в самой критической точке в нуль, должен быть учтен еще и другой член второго порядка по An, связанный с неоднородностью тела с флуктуи­рующей плотностью. Не повторяя в этой связи изложенных уже в § 146 рассуждений, сразу укажем, что это—член, квад­ратичный по первым производным от An по координатам; в изо­тропной среде такой член может быть лишь квадратом градиента. Таким образом, мы приходим к выражению вида *)

Представив теперь An в виде ряда Фурье (116,9), приведем это выражение к виду (116,10) с функцией

и затем, согласно (116,14), находим фурье-образ искомой корре­ляционной функции:

v (k)==^[at + вВц +gn_KVfi*]-* (152,18)

(ввиду малости знаменателя этого выражения, слагаемым 1 в v(&) можно пренебречь). Эта формула полностью аналогична с (146,8). Поэтому корреляционная функция v(r) в координат­ном представлении имеет тот же вид (146,11) с корреляционным радиусом

В частности, на критической изохоре (rj = 0): r_ccr>t~^X12.

§ 153. Флуктуационная теория критической точки

Полученные в предыдущем параграфе формулы позволяют установить определенную аналогию между термодинамическим описанием свойств вещества вблизи критической точки и вблизи точек фазового перехода второго рода.

^]) Тот факт, что AF_a оказалось выраженным в виде интеграла от функ­ции точки в теле (а не от функции двух точек, как в общем выражении (116,8)), связан с предположением о медленности изменения An — рассматри­ваются длинноволновые компоненты флуктуации плотности.

Для этого будем, в духе теории Ландау, сначала рассмат­ривать г) не как определенную функцию Р и Т, а как незави­симую переменную, равновесное значение которой устанавли­вается минимизацией некоторого термодинамического потенциала Ф(Р, Т, т]). Последний следует подобрать таким образом, чтобы эта минимизация действительно приводила к правильному урав-

нению состояния (152,7). Этому требованию удовлетворяет выра­жение *)

Ф (Р, Т, л) = Ф₀ (Р, Т) + 4 [- (Р-Ы) ц+atrf+В_Ч«]. (153,1)

^пкр

Сравнив (153,1) с (144,3), мы видим теперь, что существует аналогия между описанием фазового перехода второго рода во внешнем поле в теории Ландау и описанием критической точки между жидкостью и газом в ван-дер-Ваальсовой теории. При этом роль параметра порядка во втором случае играет изменение плотности вещества г\ = п—/г_кр, а роль внешнего поля — разность

h = p—bt. (153,2)

Если Ф(г, h) есть термодинамический потенциал тела вблизи точки фазового перехода второго рода (при некотором фиксиро­ванном значении давления!), то выражение <D(t, р—Ы) даст вид термодинамического потенциала вещества вблизи критической точки. Все сказанное в § 146 о способе перехода от потенциала Ф к потенциалу Q относится к любому случаю, так что аналогия остается и для потенциалов Q в обеих задачах.

В § 147 было показано, каким образом можно перейти от термодинамического потенциала Q в теории Ландау к эффектив­ному гамильтониану, описывающему фазовый переход в точной флуктуационной теории. Поэтому указанная аналогия позволяет ожидать, что и законы поведения термодинамических величин вблизи критической точки совпадают (с соответствующей заме­ной смысла т) и ft) с предельными законами во флуктуацион­ной области фазового перехода второго рода во внешнем поле (описывающегося всего одним параметром порядка).

^г) Несущественный для дальнейшего коэффициент перед квадратной скоб­кой выбран так, чтобы после минимизации выражение (153,1) переходило в правильный потенциал ф(р, т). Может показаться странным отсутствие в (153,1) симметрии относительно put, проявляющееся в отсутствии члена с р в коэффициенте при r\^z. В дей­ствительности член с т)^а существен, лишь если мал коэффициент р—bt при Г); в таком случае можно с равным правом писать ah)² или арг\^г/Ь.

Следует сразу же подчеркнуть, что такое отождествление заведомо может иметь лишь приближенный характер. В теории фазовых переходов, основанной на эффективном гамильтониане (147,6), имеет место точная симметрия по отношению к преобра­зованию h—►—h, т)—►— и (связанная с тождественным отсутст­вием члена третьего порядка ~г|⁸). В теории же критической точки такая симметрия является лишь приближенной; отсутствие в (153,1) (а потому и в эффективном гамильтониане) членов, нару­шающих эту симметрию, связано лишь с пренебрежением ими как малыми по сравнению с остальными членами. Поэтому можноутверждать лишь, что должны совпадать главные члены в пре­дельных зависимостях в обеих задачах ^[54]).

В теории фазовых переходов при t >0 и п = 0 имеем т) = 0, а при t <0 и h—>-0 находятся в равновесии две фазы с отлич­ными от нуля значениями параметра порядка и г)₂, причем r)_t = — tj₂ (точки А и А' на рис. 64,6, стр. 499); последнее ра­венство является при этом точным следствием отмеченной выше симметрии эффективного гамильтониана. В случае критической точки этим свойствам отвечает равенство

p—bt = 0, (153,3)

определяющее критическую изохору (т) = 0, т. е. п = /г_кр) при t > О и линию равновесия жидкости и пара при t < 0. Равенство же т]₂ = — г)! означает здесь симметричность линии фазового равно­весия в плоскости t, т), а продолжение аналогии позволяет утверждать, что эти значения стремятся к нулю при t—>-0 по закону

т]₁ = -Л₂~(-0^р (153,4)

с тем же показателем, что и в (148,5)^[55]). Но поскольку инвари­антность эффективного гамильтониана по отношению к изменению знака т) (при h = 0) имеет лишь приближенный характер, то воз­никает вопрос о предельном законе температурной зависимости суммы T^i + y]!- На основе сказанного до сих пор можно утверж­дать лишь, что эта величина—более высокого порядка малости, чем сами % и г|₂; мы вернемся к этому вопросу в конце пара­графа.

На рис. 74 изображена фазовая диаграмма в плоскости т), t. Область расслоения на две фазы заштрихована, а ее граница изображена симметричной кривой, как это соответствует закону (153,4).

Теплота испарения связана с разностью —т}₂ формулой (152,14). Поэтому она стремится при \t\—>-0 к нулю по тому же закону

qn>(— tf. (153,5)

Общее уравнение состояния однородного вещества во всей окрестности критической точки (в плоскости ц, Т) можно пред­ставить в виде

(153,6)

где верхний и нижний знаки относятся к т) > 0 и л < О (В. Widom, 1965). Эта формула соответствует уравнению (148,18) теории фа-

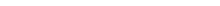зовых переходов (разрешен­ному относительно К).

К функции f(x) в (153,6) относятся такие же сообра­жения об аналитичности, о которых говорилось в § 149 в случае переходов второго рода.

Так, при заданном отлич­ном от нуля значении т] изме­нение t нигде не приводит к прохождению через кри­тическую точку, и потому значение t = 0 не является особой точкой функции (153,6). Она разложима, следовательно, по целым степеням t. Другими словами, функция f(x) разла­гается по целым степеням х. Первые члены разложения: / (х) оо 1 + с_хх, так что уравнение состояния принимает вид

P~bt™±\4_]f[\+c₁j-L_ub+...] при UKhr (153,7)

(первый член разложения соответствует определению (148,10) для случая сильного поля в теории фазовых переходов). На рис. 74 тонкими пунктирными линиями схематически показаны границы области, к которой относится это уравнение состояния. В этой области можно выделить еще два предельных случая. Если t<^p (в частности, на критической изотерме, т.е. на линии [56] = 0), то

р оо ± | т] j⁶

(153,8)

(153,9)

Если же t^>p (в частности, на критической изобаре, т. е. на линии р = 0), то

/оо±Ы^в

Сравнение (153,8) и (153,9) обнаруживает, как и следовало, сим­метрию между put¹).

Аналогичным образом при заданном отличном от нуля зна­чении t не является особой точкой нулевое значение переменной и. Поэтому при t > 0 и г)—*0 функция (153,6) разложима по целым степеням rj, причем разложение может содержать только нечет­ные степени tj,— снова ввиду симметрии эффективного гамиль­тониана относительно одновременного изменения знаков ri и ft. Отсюда следует, что¹)

/ (х)е\эхРв(_С1л:-Р+СзЛ;-³В+ • • •) при х—юо;

множитель хР^а сокращает нецелую степень т)⁶, а переменная разложения х-$сох\. Таким образом, уравнение состояния при­нимает вид

р—bteof*[c₁i\+c_ti\4—»+.. ■].при *>|т||^1/р (153,10)

(учтено равенство 66 = 6 + 7 (148,14)). Область применимости этого уравнения тоже схематически показана на рис. 74. Первый член разложения (153,10) соответствует соотношению т, = %hcvht~v теории фазовых переходов в слабом поле.

Поведение производных различных порядков от р по г) (при t = const) зависит от направления (в плоскости т|, t), по которому происходит приближение к критической точке. При приближении вдоль критической изотермы (£ = 0) функция р(п) дается форму­лой (153,8). Фактическое значение индекса 6 лежит между 4 и 5. Поэтому вдоль критической изотермы стремится к нулю не только (др/дг\)_ь но и производные нескольких следующих порядков.

При приближении к критической точке по всякому другому направлению (лежащему вне области расслоения на две фазы, т. е. вдоль лучей ^ = const -1 "П | с const > 0) выполняется нера­венство £^>|il|^l/p> поскольку фактически 1/Р > 1. Из уравнения состояния имеем тогда

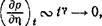
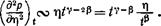
h = p—bt, (153,11)

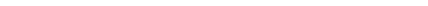
и для второй производной

написанного прямо по аналогии с формулой (149,7) теории фазовых переходов (с тождественной заменой показателей: dv = 2—а, p/v= 1/(6+у)). Не повторяя заново всех рассуждений, выпишем сразу (по аналогии с (149,9—10)) нужные для дальнейшего пре­дельные выражения ¹):

Ф (p,t) со при t>0, h—-0, (153,12)

Ф(р,Ооч_Э(-О^г-«[1+с₁р^!^] при t < 0, А—»-0. (153,13)

Двукратным дифференцированием выражения (153,12) находим теплоемкость на критической изохоре (линия р—bt = 0, >0):

С„оэ[57]-«. (153,14)

Поскольку дифференцирование при h = 0, t > 0 означает диффе­ренцирование при т] = 0, то это—теплоемкость при постоянном объеме. Таким образом, теплоемкость C_v на критической изо­хоре ведет себя как теплоемкость С_р в фазовом переходе второго рода!

Согласно формуле (16,10) имеем

г —г соЁЕЁ1&

°» (dp/dr\)f

При приближении к критической точке производная (dp/dt)^ стре­мится к постоянному пределу Ъ, в чем легко убедиться с по­мощью уравнений состояния (153,7) или (153,10). Поэтому

C^(l-);¹. (153,15)

Расходимость этого выражения при приближении к критической точке—более сильная, чем расходимость C_v; поэтому член С„ опущен по сравнению с С_р.

Наконец, остановимся на вопросе об асимметрии кривой сосу­ществования фаз вблизи критической точки (В. Л. Покровский, 1972).

Как уже было отмечено, эта асимметрия может появиться только в результате учета в эффективном гамильтониане членов, нарушающих его симметрию относительно преобразования

h—>-—h, г)—>■—г). Первый из таких членов: ^r^/i^[58]); его появ­ление можно формально представить как результат замены в эф­фективном гамильтониане t на /+ const-h; тогда

arft —+ ац^г (t+ const • Л).

Эта замена в эффективном гамильтониане приведет к такой же замене в термодинамическом потенциале, выраженном в функции от h и t:

Ф(к, t)—>0(h, t+const-h).

Вблизи кривой сосуществования фаз функция Ф (h, t) дается выражением (153,13); искомая же плотность вычисляется диф­ференцированием по h. В результате получим

Vr\\n

■±о-

-j- (2—а) ■ const • (— г)^[59] ~^а.

2>₇ Первый член дает уже известные нам значения (153,4) плотностей на симме­тричной кривой сосуществования; этот член исчезает в сумме гц + т^, для которой остается

% + Я^[60]"*, (153,16)

следует тогда прямо из точного соотношения а+2(5 + у=2.

чем и определяется искомый закон. Фактически 1—а>6^[61]), так что асимметрия действительно относительно мала: (% + т)₂)/т}₁—>-0 при t—*0. Сумма г), фактически положительна; это значит, что ее учет деформирует кривую сосуществования, как это пока­зано на рис. 75.

ГЛАВА XV

ПОВЕРХНОСТИ

§ 154. Поверхностное натяжение

Везде в предыдущем мы пренебрегали эффектами, связанными с наличием поверхностей раздела между различными телами*). Поскольку при увеличении размеров (числа частиц) тела поверх­ностные эффекты растут гораздо медленнее, чем объемные, то пренебрежение ими при изучении объемных свойств тел вполне оправдано. Существует, однако, ряд явлений, которые связаны именно со свойствами поверхностей раздела.

Термодинамические свойства поверхности раздела полностью характеризуются одной величиной (функцией состояния тел), определяемой следующим образом. Обозначим площадь поверх­ности раздела посредством § и рассмотрим процесс обратимого изменения Этой площади на бесконечно малую величину d-З. Ра­бота, затрачиваемая при таком процессе, очевидно, пропорцио­нальна dh, т. е может быть написана в виде

dR = adu. (154,1)

Определяемая таким образом величина а и представляет собой основную характеристику поверхности раздела; она называется коэффициентом поверхностного натяжения.

Формула (154,1) в точности соответствует формуле dT? = — PdV для работы при обратимом изменении объема тела. Можно ска­зать, что а играет для поверхности такую же роль, как давление для объема. В частности, легко показать, что на единицу длины контура, ограничивающего какой-либо участок поверхности раз­дела, действует сила, по величине равная а и направленная касательно к поверхности по внутренней нормали к контуру.

¹) В действительности, конечно, соприкасающиеся фазы разделены узким переходным слоем; не интересуясь его структурой, мы можем рассматрив«ть его как геометрическую поверхность.

Мы Подразумеваем при этом, что а > 0; что это действительно так, доказывают следующие соображения. Если бы было а < 0, то на ограничивающий поверхность контур действовали бы силы, направленные по внешней нормали к нему, т. е. стремящиеся «растянуть» поверхность; другими словами, поверхность раздела двух фаз стремилась бы неограниченно возрастать, т. е. фаз вообще не существовало бы, так как они смешались бы. Напро­тив при а > О поверхность раздела стремится принять наимень­шее возможное (при данном объеме обеих фаз) значение. Поэтому, например, если одна изотропная фаза погружена в другую, то она примет форму шара (при этом, конечно, мы пренебрегаем действием внешнего—гравитационного поля).

Обратимся к более подробному изучению поверхностного натяжения на границе раздела двух изотропных фаз—жидкости и пара—одного и того же чистого вещества. Если речь идет о поверхности раздела двух фаз, находящихся в равновесии друг с другом, то следует помнить, что их давление и темпера­тура связаны определенной функциональной зависимостью—урав­нением кривой фазового равновесия. При этом а является функ­цией, по существу, не от двух, а всего от одной независимой переменной.

Без учета поверхностных эффектов дифференциал энергии системы из двух фаз (одного и того же вещества) при заданном объеме V всей системы имеет вид dE = Т dS + р, dN (в равновесии температуры Т и химические потенциалы р обеих фаз одинаковы, что и дает возможность написать это равенство для всей системы сразу). При учете же наличия поверхностных эффектов к правой стороне этого равенства надо, очевидно, прибавить еще выраже­ние (154,1):

dE = TdS + ndN + ad§. (154,2)

В качестве основной термодинамической величины, однако, удобно выбрать не энергию, а потенциал Q—термодинамический потенциал по отношению к независимым переменным Т, р (и объему V). Удобство этой величины в данном случае связано с тем, что Т и р,—величины, имеющие одинаковое значение в обеих фазах (между тем как давления при учете поверхностных эффектов уже, вообще говоря, не совпадают—см. § 156). Для ее дифференциала Q (снова при V= const) имеем

dQ = — SdT—Ndp+adS. (154,3)

Термодинамические величины (такие, как Е, Q, S и т. п.) рассматриваемой системы можно представить в виде суммы двух частей—объемной и поверхностной. Такое разделение, однако, не однозначно, так как числа частиц в каждой из фаз опреде­лены лишь с точностью до числа частиц, находящихся в пере­ходном слое между фазами; то же самое относится и к объемам фаз. Между тем эта неопределенность—как раз того же порядка величины, что и интересующие нас поверхностные эффекты. Мы сделаем разделение однозначным, подчинив его следующему естественному условию: объемы V_x и V₂ обеих фаз определяются так, чтобы наряду с равенством V, f V₂ = V (где V—полный объем системы) имело место также и равенство

n,V, + n₂V₂ = N,

где N — полное число частиц в системе, а /1,-/1,(11, Т) и п₂ = = n₂(p, Т) — объемные плотности числа частиц в каждой из фаз (рассматриваемых как неограниченные). Эти два равенства фик­сируют выбор объемов V„ V₂ (и чисел частиц N, = tijV,, N₂ = n₂V₂), а тем самым и значения объемных частей всех других термоди­намических величин. Будем отмечать объемные части индексом О, а поверхностные—индексом s; для числа частиц имеем по при­нятому нами определению N_s = 0.

Из (154,3) имеем при постоянных Т и р, (а потому и постоян­ном a) dQ = ad§; поэтому ясно, что Q_s = a§. Таким образом,

Q = Q₀ + a§. (154,4)

Поскольку энтропия 5 = — ₈> ^{т0 ее} поверхностная часть¹)

Далее находим поверхностную свободную энергию; поскольку F = Q + N\i, и N_s = 0, то

F_t = ai. (154,6)

Поверхностная же энергия

E, = F, + TS_a= [*-T%r) S. (154,7)

Количество тепла, поглощающееся при обратимом изотерми­ческом изменении площади поверхности от §, до §₂, равно

Q = Т (S_S2-S_S,) = - Т^г («,-«,). (154,8)

Сумма тепла Q и работы R = a(§₂—8,) при этом же процессе равна, как и следовало, изменению энергии E_s2 — E_sl.

^х) Коэффициент а есть функция всего одной независимой переменной; для такой функции понятия частных производных по р. и по Т сами по себе не имеют смысла. Однако тем самым, что мы положили

(да/дц.)_г = 0; в э- da_ / да \ дТ~\дт)»'

Дата добавления: 2014-11-07