Ol — V2X 32 страница

вр=т|2тгФ«. С¹⁴⁵-⁸)

i

т. е. симметрию б кристалла, возникающего при переходе второго рода из кристалла с симметрией G₀ ^[3]).

Совокупность величин % играет в излагаемом формализме роль параметра порядка, описывающего отклонение несиммет­ричной фазы от симметричной. Мы видим, что в общем случае этот параметр многокомпонентен, причем отношения у,- = т]_г/г) определяют симметрию несимметричной фазы, а общий множи­тель т) дает количественную меру отклонения при заданной сим­метрии.

^х) Может оказаться, что имеется всего один инвариант четвертого порядка (2'П/)² = 'Ч⁴- В таком случае член четвертого порядка не зависит от величин у,-и для определения последних надо обратиться к членам более высокого поряд­ка, зависящим от у,-. Учет членов более высоких порядков может оказаться нужным также и в некоторых случаях, когда минимизация зависящих от у,-членов четвертого порядка обращает эти члены в нуль.

Полученные условия, однако, сами по себе все еще недоста­точны для возможности существования фазового перехода вто­рого рода. Еще одно существенное условие выясняется, если обратиться к обстоятельству (от которого мы до сих пор наме­ренно отвлекались), связанному с классификационными свойствами представлений пространственных групп^[4]). Мы видели в § 134, что эти представления классифицируются не только по дискретному признаку (скажем, номеру малого представления), но и по зна­чениям параметра к, пробегающего непрерывный ряд значений.

Поэтому и коэффициенты А^ш в разложении (145,3) должны зави­сеть не только от дискретного номера п, но и от непрерывной переменной к.

Пусть фазовый переход связан с обращением в нуль (как функции от Р и Т) коэффициента А^(п) (к) с определенным номером и и определенным значением к = к„. Для того чтобы переход действительно мог произойти, необходимо, однако, чтобы А^{а\ как функция от к, имела при к = к₀ (тем самым для всех век­торов звезды к₀) минимум, т. е. разложение Л^(п)(к) по степеням к—к₀ в окрестности к₀ не должно содержать линейных членов. В противном случае какие-то коэффициенты А^{п) (к) заведомо обратятся в нуль раньше, чем Л^(п) (к₀), и переход рассматри­ваемого типа произойти не сможет. Удобная формулировка этого условия может быть получена, исходя из следующих соображений.

Значение к₀ определяет трансляционную симметрию функций ср,-, а тем самым и функции бр (145,8), т. е. определяет периодич­ность решетки новой фазы. Эта структура должна быть устой­чива по сравнению со структурами, соответствующими близким к к„ значениям к. Но структура с k = k₀-_r-x (где х—малая величина) отличается от структуры с k = k₀ пространственной «модуляцией» периодичности последней, т.е. появлением неодно­родности на расстояниях (~1/х), больших по сравнению с пери­одами (размерами ячеек) решетки. Такую неоднородность можно описывать макроскопически, рассматривая параметры порядка % как медленно меняющиеся функции координат (в противополож­ность функциям ф,-, осциллирующим на межатомных расстояниях). Мы приходим, таким образом, к требованию устойчивости состоя­ния кристалла по отношению к нарушению его макроскопиче­ской однородности ^х).

При пространственно непостоянных величинах Г|,- плотность термодинамического потенциала кристалла будет зависеть не только от самих т|,-, но и от их производных по координатам (в первом приближении — от производных первого порядка). Соответственно этому вблизи точки перехода надо разложить Ф (единицы объема) по степеням как т],-, так и их градиентов Vn<-Для того чтобы термодинамический потенциал (всего кристалла) мог быть минимален при постоянных необходимо, чтобы в этом разложении члены первого порядка по градиентам тождественнообращались в нуль (члены же, квадратичные по производным, должны быть существенно положительными; это обстоятельство, однако, не накладывает никаких ограничений на r\_h так как такая квадратичная форма существует для %, преобразующихся по любому из неприводимых представлений).

Из линейных по производным членов нас могут интересовать только члены, пропорциональные просто дц^дх,...., и члены, содержащие произведения т]₍- дг\_к/дх,... Члены более высоких порядков, очевидно, несущественны. Минимальным должен быть термодинамический потенциал всего кристалла, т. е. интеграл

^ФйУ по всему объему. Но при интегрировании все полные производные в Ф дают постоянную, несущественную для опре­деления минимума интеграла. Поэтому можно опустить все члены в Ф, пропорциональные просто производным от п,-. Из членов же с произведениями п,- дц_к/дх,... можно опустить все симметрич­ные комбинации

dx\i. дц_к д

оставив только антисимметричные части

(Н5,9)

В разложение Ф могут войти только инвариантные линейные комбинации величин (145,9). Поэтому условие возможности фа­зового перехода состоит в отсутствии таких инвариантов.

Компоненты градиентов Vn,- преобразуются как произведения компонент вектора на величины т],-. Поэтому разности (145,9) преобразуются как произведения компонент вектора на анти-симметризованные произведения величин т|,-. Следовательно, тре­бование невозможности составления линейного скаляра из вели­чин (145,9) эквивалентно требованию невозможности составления из антисимметризованных произведений

Х#[5] = ФЛ>[6]—Ф[7]Ф< (145,10)

комбинаций, преобразующихся как компоненты вектора (здесь Фм ф;— одни и те же функции базиса данного неприводимого представления, которые представляем себе взятыми в двух раз­личных точках х, у, z и х', у', г' во избежание обращения раз­ности тождественно в нуль) [8]). Отмечая функции базиса представления двумя индексами кос (как в § 134), напишем раз­ности (145,10) в виде

%ка, к'В =Фкаф'к'р— ф'каФк'в, (145,11)

где к, к',... —векторы одной и той же звезды.

Пусть вектор к занимает наиболее общее положение и не обладает никакой собственной симметрией. Звезда к содержит, по числу поворотных элементов группы, п векторов (или 2п, если пространственная группа сама по себе не содержит инверсии), причем наряду с каждым к имеется отличный от него вектор —к. Соответствующее неприводимое представление осущест­вляется столькими же функциями фи (по одной для каждого к, ввиду чего индекс а опускаем). Величины

Xk, -к = фкф'~к — фкф-к (145,12)

инвариантны по отношению к трансляциям. При воздействии же поворотных элементов эти п (или 2п) величин преобразуются друг в друга, осуществляя представление соответствующей точеч­ной группы (кристаллического класса) с размерностью, равной порядку группы. Но такое (так называемое регулярное) пред­ставление содержит в себе все неприводимые представления группы, в том числе и те, по которым преобразуются компо­ненты вектора.

Аналогичные рассуждения доказывают возможность состав­ления вектора из величин %ка, __кв и в случаях, когда группа вектора к содержит одну ось и проходящие через нее плоскости симметрии.

Эти рассуждения становятся, однако, неприменимыми, если группа вектора к содержит оси, пересекающиеся друг с другом или с плоскостями симметрии, или содержит инверсию (о Таких группах будем говорить, что они обладают центральной точкой). В этих случаях вопрос о возможности составления вектора из величин (145,11) нуждается в специальном рассмотрении в каждом конкретном случае. В частности, такой вектор заведомо не может быть составлен, если группа к содержит инверсию (так что к и —к эквивалентны), а каждому к в звезде отвечает всего по одной функции ф_к: в этом случае не существует таких %_кк-, которые были бы инвариантны по отношению к трансляциям, как это во всяком случае должно было бы быть для компонент вектора.

Таким образом, сформулированное требование очень сильно ограничивает возможные изменения симметрии при фазовом переходе второго рода. Из всего бесконечного числа различных неприводимых представлений группы О₀ надо рассматривать лишь сравнительно небольшое число тех, для которых группа вектора к обладает центральной точкой.

Такую собственную симметрию могут иметь, разумеется, лишь векторы к, занимающие определенные исключительные положения в обратной решетке; их составляющие равны при этом определенным долям (1/2, 1/3, 1/4), основных периодов обратной решетки. Это значит, что изменение трансляционной симметрии кристалла (т. е. его решетки Бравэ) при фазовом переходе второго рода может состоять лишь в увеличении тех или иных из основных периодов в небольшое число раз. Иссле­дование показывает, что в большинстве случаев возможное из­менение решетки Бравэ заключается в удвоении периодов. Кроме того, в объемноцентрированных (ромбической, тетрагональной, кубической) и в кубической гранецентрированной решетках воз­можны изменения с учетверением некоторых периодов, а в ге­ксагональной решетке—с утроением периода. Объем элемен­тарной ячейки при этом может увеличиться в 2,4, 8 раз; в гра­нецентрированной кубической решетке есть также случаи, увеличения в 16 и 32 раза, а в гексагональной — в 3 раза и 6 раз.

Разумеется, возможны переходы и без изменения решетки Бравэ (им соответствуют неприводимые представления с к = 0). При этом изменение симметрии состоит в уменьшении числа поворотных элементов, т.е. меняется кристаллический класс¹).

Отметим следующую общую теорему: фазовый переход вто­рого рода может существовать для всякого изменения структуры, связанного с уменьшением вдвое числа преобразований симмет­рии (такое изменение может произойти либо путем увеличения вдвое элементарной ячейки при неизменном кристаллическом классе, либо путем уменьшения вдвое числа вращений и отра­жений при неизменной элементарной ячейке). Доказательство основано на том, что если группа О₀ имеет подгруппу G вдвое меньшего порядка, то среди неприводимых представлений (?„ во всяком случае имеется одномерное представление, осущест­вляемое функцией, инвариантной относительно всех преобразо­ваний подгруппы G и меняющей знак при всех остальных пре­образованиях группы G₀. Ясно, что в таком случае инварианты нечетных порядков отсутствуют, а величин типа (145,11) из одной функции вообще нельзя составить.

Справедлива, по-видимому, также и следующая теорема: фазовые переходы второго рода не могут существовать для из­менений структуры, связанных с уменьшением числа преобразо­ваний симметрии в три раза (благодаря наличию членов треть­его порядка в разложении Ф).

Наконец, в качестве иллюстрации конкретных применений изложенной общей теории рассмотрим возникновение упорядо-

*) Возможные случаи такого рода — см. В. Л. Инденбом, Кристаллогра­фия 5, 115 (1960).

чения в сплавах, которые в неупорядоченном состоянии имеют объемноцентрированную кубическую решетку с атомами в вер­шинах и центрах кубических ячеек (как на рис. 61, б)¹). Задача заключается в определении возможных типов упорядочения (т. е., как говорят в кристаллографии, сверхструктур), которые могут возникнуть в такой решетке при фазовом переходе второго рода.

Для объемноцентрированной кубической решетки обратная решетка является гранецентрированной кубической. Выберем ребро кубической ячейки прямой решетки в качестве единицы длины. Тогда ребро кубической ячейки обратной решетки равно 2-2я. В этой обратной решетке следующие векторы к обладают группами собственной симметрии с центральной точкой:

(a) (0, 0, О)-0_А,

(b) (1/2, 1/2, 1/2)- О_н,

(c) (1/4, 1/4, 1/4), (-1/4, -1/4, -1/4)-7,, (145,13)

(d) (0, 1/4, 1/4), (1/4, 0, 1/4), (1/4, 1/4, 0),

(0, 1/4, -1/4), (-1/4, 0, 1/4), (1/4, -1/4, 0)-D_№.

Здесь указаны компоненты векторов к вдоль ребер кубиче­ской ячейки обратной решетки (оси х, у, г), измеренные в долях этих ребер; для того чтобы получить векторы к в выбранных выше единицах, надо умножить эти числа на 2-2я = 4я. В (145,13) перечислены лишь неэквивалентные векторы, т. е. векторы каж­дой звезды к.

Дальнейшее исследование очень упрощается благодаря тому, что для решения поставленного вопроса оказывается необходи­мым рассматривать не все малые представления. Дело в том, что мы интересуемся лишь теми возможными изменениями сим­метрии, которые могут быть реализованы возникновением сверх­структуры, т. е. упорядоченным расположением атомов по су­ществующим в решетке узлам без их относительного смещения. В данном случае элементарная ячейка неупорядоченной решетки содержит всего один атом. Поэтому появление сверхструктуры может означать лишь возникновение неэквивалентности узлов различных ячеек. Это значит, что возникающее изменение функ­ции распределения плотности бр должно быть инвариантно от­носительно всех поворотных преобразований группы к (без одно­временной трансляции). Другими словами, допустимо только единичное малое представление. Соответственно этому в базис­ных функциях (134,3) можно заменить и_а единицей.

Рассмотрим теперь поочередно перечисленные в (145,13) звезды к.

) Такая решетка относится к симморфной пространственной группе 0\.

(a) Функция с к = 0 обладает полной трансляционной инва­риантностью. Другими словами, в этом случае элементарная ячейка не меняется, а поскольку каждая ячейка содержит всего по одному атому, то не может быть вообще никакого изменения симметрии.

(b) Этому к соответствует функция ехр 2ni (x-\-y-\-z). Линей­ная комбинация (этой функции и функций, получающихся из нее при всех вращениях и отражениях), обладающая симметрией O_h группы к, есть

<p = cos2nxcos2ni/cos2n2. (145,14)

Симметрия возникающей фазы есть симметрия функции плотно­сти р = р₀ + бр, 6р = т]ф¹). Функция ф инвариантна относительно всех преобразований класса O_h и относительно трансляций вдоль любого ребра кубической ячейки, но не относительно трансляции на половину ее пространственной диагонали (1/2 1/2 1/2). По­этому упорядоченная фаза имеет простую кубическую решетку Бравэ с двумя неэквивалентными узлами в элементарной ячейке (ООО) и (1/2 1/2 1/2), которые будут заняты различными ато­мами. Сплавы, которые могут быть вполне упорядочены по этому типу, относятся к составу АВ (как, например, упомянутый в § 142 сплав CuZn).

(c) Соответствующие этим векторам к функции, обладающие
симметрией T_d, таковы:

ф_х = cos itxcos ш/ cos nz, ф₂ = sin ял; sin яг/sin яг. (145,15)

Из них можно составить два инварианта четвертого порядка: (ф? + ф1)^{г и} (ф! + ф|). Поэтому разложение Ф (145,7) имеет вид

Ф = Ф₀ + A if + ад + В₂ц* (у{ + у*). (145,16)

Здесь надо различать два случая. Пусть В₂ < 0; тогда Ф как функция от 7_Х, у₂ при дополнительном условии у| -f- у\ = 1 имеет минимум при 7_Х=1, 72 = 0- Функция бр = т)ф₁ имеет симметрию класса O_h с гранецентрированной решеткой Бравэ, кубическая ячейка которой в восемь раз превышает по объему кубическую ячейку первоначальной решетки. Элементарная ячейка содержит четыре атома (а кубическая ячейка—16 атомов). Поместив в эк­вивалентные узлы одинаковые атомы, найдем, что эта сверхструк­тура соответствует тройному сплаву состава АВС₂ с атомами в следующих положениях:

4А(0 0 0), (0 1/2 1/2; О, 4В (1/2 1/2 1/2), (0 0 1/2; О. 8С(1/4 1/4 1/4), (3/4 3/4 3/4), (1/4 3/4 3/4; Q, (1/4 1/4 3/4; Q

^х) Это не означает, разумеется, что изменение бр в реальном кристалле дается именно написанной функцией (145,14). В выражении (145,14) существенна только его симметрия.

	------ _	>'—^
J <•		, с
	_J_L >----	г..	1.1

Рис. 65.

имеет симметрию O_h с той же гранецентри-

Эта функция класса

рованной решеткой Бравэ, что и в предыдущем случае, но лишь с двумя наборами эквивалентных узлов, которые могут быть заняты двумя родами атомов А и В:

8А(0 0 0), (1/4 1/4 1/4),

(1/4 3/4 3/4; С). (0 1/2 1/2; Q,

8В (1/2 1/2 1/2), (3/4 3/4 3/4),

(1/4 1/4 3/4; С), (0 0 1/2; Q

(рис. 65, б).

(d) Этим векторам к соответ­ствуют следующие функции с тре­буемой симметрией D_2h:

Ф! = созя(г/—г), ф₃ = cos я (х—у),

Ф₂ = созя(^ + г), ф₄ = cos я (*+!/),

Из них можно составить один инвариант третьего порядка и четыре инварианта четвертого порядка, так что разложение (145,6) принимает вид

ф = ф₀ + Ах? + Crf (yjysys + YsYsYe + YiY.Ye + y»y«Ti) + w + + В, ч* {yi + yl+у}+yi + yi + yi) + B,i\* (у!?! + y!?2 + ym) +

+ B_ti\* (YiYaYsY* + YeYaY&Ye + YiYsYsYe)-

Ввиду наличия кубических членов фазовый переход второго рода в этом случае невозможен. Для исследования возможности су­ществования и свойств изолированных точек непрерывного пе-

J) Тот факт, что в обоих случаях у, и у₂ оказались просто числами—ре­зультат наличия лишь одного (зависящего от y_lt у₂) члена в Ф. При большем числе различных инвариантов четвертого порядка среди минимизирующих Ф на­боров yi могли бы быть и зависящие от Р, Т.

рехода (см. § 150) надо было бы исследовать поведение функ­ции Ф вблизи ее минимума; мы не станем останавливаться здесь на этом.

На данном примере мы видим, насколько жесткие ограниче­ния накладывает термодинамическая теория на возможность фазовых переходов второго рода; так, в данном случае они мо­гут существовать лишь для образования сверхструктур трех типов!).

Обратим внимание также и на следующее обстоятельство. В случае (с) (при В_г < 0) фактическое изменение функции плот­ности бр = г|ф₁ отвечает только одному из двух фигурирующих в термодинамическом потенциале (145,16) параметров у₁₉ у₂. Этим демонстрируется важная черта изложенной теории: при рассмотре­нии какого-либо конкретного изменения решетки при фазовом переходе второго рода может оказаться необходимым учитывать также и другие, «виртуально возможные» изменения.

§ 146. Флуктуации параметра порядка

Уже неоднократно указывалось, что самая точка фазового перехода второго рода является в действительности особой точ­кой для термодинамических функций тела. Физическая природа этой особенности состоит в аномальном возрастании флуктуации параметра порядка, в свою очередь связанном с уже упоминав­шейся пологостью минимума термодинамического потенциала вблизи точки перехода. Легко найти закон этого возрастания (в рамках рассматриваемой теории Ландау). При этом будем считать, что изменение симметрии при переходе описывается всего одним параметром г).

Минимальная работа, требуемая для вывода системы из равновесия при заданных постоянных значениях давления и тем­пературы, равна изменению АФ„ ее термодинамического потен­циала ²). Поэтому вероятность флуктуации при постоянных Р и Т:

шел ехр (— АФ_П/Г).

(146,1)

Будем обозначать в этом параграфе равновесное значение пара­метра т) как п. При малом отклонении от равновесия

С помощью (144,6) выразим производную д²Ф_п/дт)² через воспри­имчивость вещества в слабом поле согласно определению (144,7). Тогда вероятность флуктуации (при температурах вблизи точки перехода Т_с) запишется в виде

(т)—г|)² V

Отсюда средний квадрат флуктуации ^х)

<(Дг|)²> = ^

(146,2)

Согласно (144,8) он возрастает при Т—+Т_с как l/t.

Для более глубокого выяснения характера и смысла этой расходимости, определим пространственную корреляционную функцию флуктуации параметра порядка. При этом нас будут интересовать длинноволновые флуктуации, в которых флуктуи­рующая величина медленно меняется вдоль объема тела; именно такие флуктуации, как мы увидим ниже, аномально возрастают вблизи точки перехода.

Для неоднородного тела (каковым оно является при учете неоднородных вдоль его объема флуктуации) термодинамический потенциал тела должен был бы быть представлен в виде интеграла

Ф„= \ Ф dV от плотности потенциала—функции координат точки в теле. Но при описании термодинамического состояния потен­циалом Ф заданным является число частиц N в теле, но не его объем (зависящий от Р и Г). Поэтому целесообразно перейти к описанию другим потенциалом, относящимся к некоторому заданному выделенному в среде объему V (содержащему пере­менное число частиц N). Таким потенциалом является Q_n(T, р)— функция температуры и химического потенциала р (при задан­ном V); роль переменной Р при этом принимает переменная с аналогичными свойствами—р (как и Р, величина, остающаяся постоянной вдоль равновесной системы).

Вблизи точки перехода зависящие от т) члены разложения функции Ф (Р, Т, г)) (144,3) представляют собой малую добавку к Ф₀ (Р, Т) (причем, после определения ц путем минимизации, остающиеся члены—одного порядка величины). Согласно теореме о малых добавках можно поэтому сразу написать такое же разложение для потенциала Й(р, Т, ц):

П(ц, Т, r_]) = Q₀(ii,T) + atrf + br\ [9] -r\h, (146,3)

с теми же коэффициентами, но лишь выраженными через другую переменную — р вместо Т (потенциал Q отнесен здесь к единице объема, так что коэффициенты в нем: a = a/V, b = B/V) ^[10] ).

Разложение (146,3) относится к однородной среде. В неодно­родном же теле оно содержит не только различные степени са­мой величины г), но и ее производных различных порядков по координатам. При этом для длинноволновых флуктуации можно ограничиться в разложении лишь членами с производными наи­более низкого порядка (и наиболее низких степеней по ним). Члены, линейные по производным первого порядка, т. е. члены вида / (г|) dr\/dx_h при интегрировании по объему преобразуются в интегралы по поверхности тела, представляющие собой не ин­тересующий нас поверхностный эффект^[11]). То же самое относится и к членам вида const д ^[12] г\/дх,dx_k. Поэтому первые члены, кото­рые должны быть учтены в разложении & по производным, это члены, пропорциональные

д^[13]г\ дц дг\

чз—зг-t или -г^[14]--^-

' дх, dxk дх; дхь

При этом первые из них при интегрировании по объему сводятся ко вторым. Окончательно находим, что написанную выше функ­цию Q надо дополнить членами вида

^(Р,Т)^ (146,4)

(как всегда, по дважды повторяющимся векторным индексам подразумевается суммирование). Мы ограничимся ниже простей­шим случаем (отвечающим кубической симметрии при г) = 0), когда gib=[15]g&ik; уже в этом случае проявляются все характер­ные свойства корреляционной функции. Таким образом, напишем плотность термодинамического потенциала в виде

Q=Q₀+rti?+bi\ [16] +g(j±y-i\h. (146,5)

Очевидно, что для устойчивости однородного тела должно быть g > 0; в противном случае Q„ не могло бы иметь минимума при т) •= const.

Рассматривая флуктуации при заданных р и Т, надо писать их вероятность в виде

дасчэехр (—AQ„/T),

поскольку минимальная работа, требуемая в этих условиях для вывода системы из равновесия есть R_min = —AQ„^[17]).

Рассмотрим для определенности флуктуации в симметричной фазе (в отсутствие поля h); тогда г| = 0, так что Дт) = т|. Огра­ничиваясь членами второго порядка по флуктуациям, напишем изменение потенциала Q„ в виде ^[18])

AQ„ = j [at (At,)^[19] +g (^)*] dV. (146,6)

Далее, поступим аналогично тому, как это делалось в § 116. Разложим флуктуирующую величину Ат] (г) в ряд Фурье в объ­еме V:

Ат] = 2 АЛке^Лг, Ar]__fc=Ari_k. (146,7)

Ее градиент

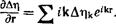
к

При подстановке этих выражений в (146,6) интегрирование по объему обращает в нуль все члены, за исключением лишь тех, которые содержат произведения tjиЛ—ь = I Ль |^а- В результате получим

AQ_n = V2№ + a')l Д%|^[20]

к

и отсюда

<[Ar₁kl^[21]> = _2t/J_+g0 (146,8)

(ср. переход от (116,10) к (116,12)). Мы видим, что при t—»0 действительно возрастают именно длинноволновые флуктуации с k^Vat/g^[22]). Подчеркнем, что сама формула (146,8) приме­нима лишь при достаточно больших длинах волн 1/k,— во вся­ком случае больших по сравнению с межатомными расстояниями. Введем обозначение для искомой корреляционной функции:

G(r) = <Ati(r₁)Ati(r_i)>, r = r₁—r₂. (146,9)

Она вычисляется как сумма

G(r) = 2<| Atikl^e'*

k

или, переходя к интегрированию по к-пространству,

G(r) = J<|Ar,_k|²>e^|g-. (146,10)

Используя формулу фурье-преобразования, указанную в приме­чании на стр. 390, находим (при гфО)

где

(146,12)

Величину г_с называют корреляционным радиусом флуктуации; им определяется порядок величины расстояний, на которых корреляция существенно убывает. При приближении к точке перехода корреляционный радиус возрастает как \IV t, а в са­мой этой точке корреляционная функция убывает как 1/г.

При г —0 интеграл (146,10) определяет средний квадрат флуктуации параметра ц в бесконечно малом элементе объема; он расходится при больших k. Эта расходимость, однако, связана просто с неприменимостью в этой области выражения (146,8) (относящегося к длинноволновым флуктуациям), и означает лишь наличие в <(Ат|)²> члена, не зависящего от t.

Подчеркнем, во избежание недоразумений, что ранее напи­санное выражение (146,2) определяет флуктуации параметра т], усредненного по объему V, линейные размеры которого 1^>г_с\ эту величину можно обозначить как <(Дт,)²>у. Среднее значение функции Аг|(г) по объему V есть как раз фурье-компонента Ar)k=o; поэтому естественно, что при& = 0 выражение (146,8) сов­падает с (146,2). Последнее можно получить также из корреля­ционной функции по очевидной формуле

<(Ar,)*>_v = -jL J <Дг, (rj Дг) (г,)>аУ, dV_t = ~ j G (г) dV, (146,13) применимой при любом конечном объеме V. Отметим, что в самой точке г=0 (где Gcol/r) этот интеграл пропорциона­лен 1/1, где /—линейные размеры участка, в котором рассмат­риваются флуктуации. При этом средний квадрат <(Дт])²>у за­висит не только от объема, но и от формы участка.

Мы можем теперь сформулировать условие, определяющее область применимости развитой здесь теории флуктуации, осно­ванной на разложении (146,5). В качестве такого условия сле­дует потребовать, чтобы был мал (по сравнению с характер­ным значением rf ~ a\t\/b) средний квадрат флуктуации пара­метра г|, усредненного по корреляционному объему. Эта вели­чина получается из (146,2) при V ~ г?, и мы приходим к условию

Ч<Ц^> (146,14)

или (взяв % и г_с из (144,8) и (146,12))

T²h2

«l'l>7" (146,15)

А. П. Леванюк, 1959; В. Л. Гинзбург, I960)^[23]).

Определение температурных зависимостей в полученных выше формулах требовало также и разложения по степеням t = T—T_c (в коэффициентах разложения по г\). Допустимость такого раз­ложения требует соблюдения условия t<^T_c, а для его сов­местности с условием (146,16) во всяком случае необходимо, чтобы было

"^<1- (146,16)

²) Для переходов, описывающихся несколькими параметрами порядка, уста- новление всех условий применимости теории Ландау требует, однако, более детального исследования.

Условия (146,14—16), обеспечивая достаточную малость флук­туации, являются в то же время условием применимости всей вообще теории фазовых переходов Ландау, изложенной в пре­дыдущих параграфах. Мы видим, что лишь при соблюдении неравенства (146,16) существует температурная область, в кото­рой эта теория справедлива. В таких случаях остаются в силе выводы теории относительно правил отбора допустимых измене­ний симметрии при переходах *). Но в отношении температурной зависимости термодинамических величин все равно неизбежно имеется узкая область вблизи Т_с, в которой теория Ландаунеприменима. Выводы этой теории надо, следовательно, относить лишь к состояниям обеих фаз вне указанного интервала темпе­ратур. Так, полученные в § 143 выражения для скачков термо­динамических величин надо понимать как разности их значений на обеих границах этого интервала. Непосредственную окрест­ность точки Т_с, отвечающую обратному знаку в неравенстве (146,15), будем называть флуктуационной; флуктуации играют здесь определяющую роль.

Дата добавления: 2014-11-07