Ol — V2X 30 страница

Свойство, о симметрии которого при этом идет речь, можно сформулировать как взаимную корреляцию между положениями

^г) Корреляционная функция такого вида была найдена Райсом (Т. М. Rice, 1965) для другого двумерного объекта (двумерного сверхпроводника), а для двумерной решетки—В. Л. Березинским (1971).

различных атомов. Пусть p₁₂dV₂ есть вероятность нахождения атома 2 в элементе объема dV₂ при заданном положении атома 1 (при этом обычно речь идет об атомах различного сорта); р₁₂ есть функция от координат r_t и г₂ двух атомов, и свойства симметрии этой функции определяют симметрию тела (у которого p=const).

Постоянство функции плотности р означает, что перемещение частей тела друг относительно друга (без изменения их объема) не приводит к какому-либо изменению равновесного состояния тела, т. е. изменению его термодинамических величин. Это есть как раз то свойство, которое характеризует жидкости (как и газы). Поэтому тела с р = const и анизотропной функцией кор­реляции р₁₂ представляют собой определенную категорию жидких кристаллов — анизотропных текучих тел. С более наглядной точки зрения это тела с анизотропным распределением молекул по их ориентации в пространстве.

В смысле симметрии этого распределения возможны две кате-гории случаев. В одной из них (так называемые нематические жидкие кристаллы) корреляционная функция зависит только от разности r₁₂ = r_t—г₂; при изменении длины вектора г₁₂ и сохране­нии его направления она не обнаруживает никакой периодичности (хотя и может испытывать колебания, затухающие по мере уве­личения г₁₂). Другими словами, такая функция не имеет трансля­ционной симметрии, и ее группа симметрии может складываться лишь из различных поворотов и отражений, т. е. представ­ляет собой какую-либо из точечных групп. С чисто геомет­рической точки зрения это может быть любая из точечных групп с осями симметрии произвольного порядка. По-видимому, однако, все известные нематические жидкие кристаллы имеют ось полной аксиальной симметрии, причем оба направления вдоль этой оси эквивалентны. Такими свойствами обладают точечные группы С» л, D_K, Dvh¹)- Мы увидим, однако, в следующем параграфе, что симметрия D_K (не содержащая никаких плоскостей симмет­рии) приводит к неустойчивости состояния жидкого кристалла, в результате чего автоматически появляется определенная «вто­ричная» периодическая структура, характерная для жидких крис­таллов другой категории—так называемых холестерических.

Помимо двух перечисленных категорий, существуют еще и дру­гие анизотропные жидкие вещества разнообразной слоистой структуры, которые принято объединять в группу смектических жидких кристаллов. По-видимому, по крайней мере некоторые из них представляют собой тела с функцией плотности р(х), периодической лишь в одном направлении. Такие тела можно

^х) В остальных группах аксиальной симметрии (С*,, C«,_v) оба направления вдоль оси не эквивалентны. Такие жидкие кристаллы были бы, вообще говоря, пироэлектрическими.

представлять себе как состоящие из свободно смещающихся друг относительно друга плоских слоев, расположенных на одинако­вых расстояниях друг от друга. В каждом из слоев молекулы ориентированы упорядоченным образом, но расположение их центров инерции беспорядочно.

В § 137 было показано, что структуры с одномерной периодич­ностью функции плотности размываются тепловыми флуктуациями. Расходимость- этих флуктуации, однако, лишь логарифмическая. Хотя этим исключается возможность одномерной периодичности, простирающейся на сколь угодно большие расстояния, но не исключается (как уже было отмечено в конце § 137) возможность ее существования в сравнительно небольших, но все же макро­скопических участках пространства.

Наконец, упомянем, что у обычных изотропных жидкостей тоже существует два различных типа симметрии. Если жидкость состоит из вещества, не имеющего стереоизомеров, то она пол­ностью симметрична не только по отношению к повороту на любой угол вокруг любой оси, но и по отношению к отражению в любой плоскости; другими словами, ее группа симметрии есть полная группа вращений вокруг точки, дополненная центром симметрии (группа K_h). Если же вещество имеет две стереоизо-мерные формы, причем жидкость содержит молекулы обоих изо­меров в различных количествах, то Жидкость не будет обладать центром симметрии (а потому не будет допускать и отражений в плоскостях); ее группа симметрии будет просто полной груп­пой вращений вокруг точки (группа К).

§ 140. Нематические и холестерические жидкие кристаллы

Ориентационная симметрия нематических жидких кристаллов является одноосной: в каждой точке жидкости существуют всего одно выделенное направление ориентации молекул,— направле­ние оси аксиальной симметрии. Поэтому макроскопическое со­стояние такого тела можно описать заданием в каждой его точке одного единичного вектора п (г), определяющего указанное на­правление; этот вектор называют директором. В полностью равновесном состоянии тело однородно, т. е. n = const. Неодно­родные же распределения п (г) описывают различные деформи­рованные состояния жидкого кристалла.

При макроскопической деформации п(г) медленно меняется вдоль тела (характерные размеры деформации велики по срав­нению с молекулярными размерами). Поэтому производные функ­ции п(г) по координатам являются малыми величинами, тем более высокого порядка малости, чем выше порядок производ­ной. Представив полную свободную энергию деформированного жидкого кристалла (при заданной температуре) в виде интеграла

F„= 5 FdV, разложим плотность свободной энергии F по степеням производных функций п(г) (С. W. Oseen, 1933; F. С. Frank, 1958).

Разложение скалярной величины F может содержать лишь скалярные же комбинации компонент вектора п и его производ­ных. Существует всего две скалярные комбинации, линейные по первым производным: истинный скаляр divn и псевдоскаляр nrotn. Из них первый при интегрировании по объему преобра­зуется в интеграл по поверхности тела и, таким образом, несу­ществен при рассмотрении объемных свойств вещества.

Истинные скаляры, квадратичные по первым производным, можно получить, написав тензор четвертого ранга

дп/с дгц дх_{ дх_т

и образуя из него инварианты путем сворачивания по парам индексов или умножением на компоненты вектора п. При этом надо учесть, что вектор п единичный, и поэтому

4-_n* = 2n_kp- = Q.
dxi ^к дх[

Таким путем найдем инварианты Но два последних отличаются друг от друга лишь дивергенцией:

дп; дщ dnit дгц_________ д! дп_кdrij

дх{ дх_к dxi dx/g дх; \ ' дх_к ^Пк дх_к

так что их вклады в полную свободную энергию отличаются лишь не интересующим нас интегралом по поверхности тела (У. L. Ericksen, 1962). Инвариант же¹)

^-^- = (nrotn)² ₊ (divn)»,

так что в качестве независимого можно выбрать (n rot п)^а. Нако­нец, можно построить квадратичный по первым производным псевдоскаляр: (nrotn)div п²).

*) Произведение же ((пу) п) rot п = 0, поскольку из уп² = 0 следует, что (ny) п = — [п rot п].

К величинам того же порядка малости относятся скаляры, линейные по вторым производным; все такие величины, однако, путем интегрирования по частям сводятся к членам, квадратич­ным по первым производным.

Таким образом, мы приходим к следующему выражению для плотности свободной энергии жидкого кристалла:

f=_Fo+bnrot n +1 (div n)² +f (n rot n)² +1 ((nV) n)² +

+ a₁₂(nrotn)divn, (140,1)

где b, a_lt a₂, a₃, a₁₂ — постоянные (функции температуры).

Как уже было указано в предыдущем параграфе, во всех известных жидких кристаллах рассматриваемых категорий направ­ления п и —п эквивалентны; для соблюдения этого требования надо положить а₁₂ = 0. Далее, если среди элементов симметрии кристалла есть плоскости, то должно быть Ь = 0. Действительно, поскольку nrotn — псевдоскаляр, а свободная энергия — истинный скаляр, то псевдоскаляром должен быть и коэффициент Ь. Но среда, имеющая плоскости симметрии, не может характеризо­ваться псевдоскалярными величинами, так как отражение в пло­скости привело бы к равенству 6 = — Ъ. Таким образом, свобод­ная энергия нематического жидкого кристалла:

F = F₀ +1 (div n)² + ^af (n rot n)² + & ((nV) n)². (140,2)

Все три коэффициента a_lt a₂, a₃ должны быть положительными. Тогда равновесному состоянию отвечает n = const.

Если же жидкий кристалл не имеет плоскостей симметрии, то ЬФО¹). Перепишем тогда (140,1) (с а₁₂ = 0) в виде

F = F₀ + Y (div п)² + f (n rot n + _?0)² + f ((nV) n)², (140,3)

где q„ = b/a₂ (а постоянная—b²/2a₂ включена в F_a). Равновес­ному состоянию такого вещества отвечает распределение направ­лений директора, для которого

divn = 0, (nV)n = 0, nrotn = — q₀.

Эти уравнения имеют решение

п_х = 0, n,, = cos <7_e#, n₂ = smq_ax. (140,4)

^х) Такой симметрией во всяком случае будет обладать жидкий кристалл, состоящий из одного стереоизомера вещества с зеркально асимметричными мо­лекулами (именно таковы все известные холестерические жидкие кристаллы). Кристаллы, состоящие из двух различных стереоизомеров одного и того же вещества, отличаются знаком постоянной Ь.

Эту структуру (отвечающую холестерическим жидким кри­сталлам) можно представить себе как результат равномерного закручивания вокруг оси х нематической среды, первоначально ориентированной своими n = const в одном направлении в пло­скости у, г. Ориентационная симметрия холестерического кри­сталла оказывается периодической вдоль одного направления (ось х) в пространстве (так что корреляционная функция р₁₂ = =р₁₂ (х, г₁₂)). Вектор п возвращается к прежнему значению через каждый интервал длины 2n/q₀ вдоль оси х; но поскольку направ­ления пи —п физически эквивалентны, истинный период по­вторяемости структуры равен n/q₀. Об описанной таким образом структуре обычно говорят как о геликоидальной.

Разумеется, изложенная теория справедлива, лишь если период геликоидальной структуры велик по сравнению с молекулярными размерами. Это условие фактически выполняется в холестери-ческих жидких кристаллах (период n/q₀~ 10^—5 см).

§ 141. Флуктуации в жидких кристаллах

Рассмотрим флуктуации, испытываемые направлением дирек­тора п в нематическом жидком кристалле (P. G. de Gennes, 1968).

Представим п в виде n = n₀ + v, где п₀ = п —постоянное вдоль всего объема равновесное направление, a v = An—флуктуацион-ное отклонение от этого значения. Поскольку п² = п;=1, то n₀v да 0, т. е. вектор v перпендикулярен к п₀. Соответственно этому корреляционная функция флуктуации

^aWVpOg) (141,1)

представляет собой двумерный тензор в плоскости, перпендику­лярной к п₀ (а, В — векторные индексы в этой плоскости). В одно­родной, но анизотропной жидкости эта функция зависит не только от величины, но и от направления вектора г = г₂—г,.

Сильное влияние на флуктуации директора оказывает магнит­ное поле. Этот эффект связан с появлением в плотности свобод­ной энергии жидкого кристалла дополнительного члена вида

^магн=—\ (ПН)², (141,2)

зависящего от самого вектора п, а не от его производных, как в (140,2)^х). Если ia > 0, то равновесное направление п совпа­дает с направлением поля, а если %_д < 0, то оно лежит в пло­скости, перпендикулярной к полю. Будем считать для опреде­ленности, что Ха > 0> ^{так что n}ol|H. Тогда (nH)²«:H^s(l — v²); опустив не зависящий от v член, пишем:

*) В одноосной анизотропной среде магнитная восприимчивость представ­ляет собой тензор вида %(A⁼⁼%<A'ft + Xaⁿiⁿfc> а намагниченность вещества при­вносит в его свободную энергию вклад—%f*#i#/&/2. Величина (141,2) есть за­висящая от п часть этого вклада.

F_KaTH = ^H*v\ (141,3)

Взяв F из (140,2) и (141,3) и сохранив лишь величины вто­рого порядка по V, получим следующее выражение для изме­нения полной свободной энергии при флуктуации:

AF„ = 1 J| a, (di v v)² + а₂ (rot, v)² + а₃ (' g.) * + _Ха H²v² }dV (141,4)

(ось х выбрана в направлении п₀). Подчеркнем, что, используя выражение (140,2) для энергии деформированного кристалла, мы тем самым ограничиваемся рассмотрением флуктуации с большими (по сравнению с молекулярными размерами) длинами волн.

Далее поступаем подобно тому, как это уже делалось в § 116. Представляем флуктуирующую величину v (г) в виде ряда Фурье в объеме V:

v = Sv_ke^ikf, v__k = v_k. (141,5)

k

После подстановки этого ряда выражение (141,4) разобьется на сумму членов (AF„)k, каждый из которых зависит только от компоненты Vk с определенным значением к. Выбрав плоскость ху так, чтобы она проходила через направление к(и Н), получим

(AF„)_k = ^{(fl^ + a_S^ + X_s№) I v_yk |² + (a₂kl + a₃k_x + _ХаЯ²) | v_2k |²}.

<Кк|²>:

Отсюда (ср. § 116) находим для средних квадратов флуктуации

Т

У(_а1к1 + а₃к²_х + ХаН*) '

<|v_2k|²>:

Z_______ ___________ (141,6)

'v(a₂k$ + a₃ki+_%aH*) ' <Vj,_kv_2k> = 0.

^х) Такой характер флуктуации аналогичен поведению флуктуации плот­ности обычной жидкости вблизи ее критической точки, или флуктуации пара­метра порядка вблизи точки фазового перехода второго рода (см. ниже §§ 146, 152). В то время, как в последних случаях роль подавляющего флуктуации фактора играет «расстояние» до указанных точек, здесь эту роль играет не за­висящий от температуры фактор—внешнее магнитное поле. Отметим_: что имен­но возрастание флуктуации п при малых к позволяет рассматривать эти флук­туации независимо от флуктуации других величин. В этой связи существенно,

Мы видим, что в отсутствие поля флуктуации фурье-компо-нент Vk неограниченно возрастают при к—>0 (интегралы же по d³k, определяющие средний квадрат самого вектора v, остаются конечными). Наложение магнитного поля подавляет флуктуации с волновыми векторами k sg# (%_a/d)^1/2 (где а—порядок величины коэффициентов a_lt а₂, а^¹).

ром п; пусть это направление нормально к поверхности слоя. При флуктуации происходит деформирование поверхности слоев и поворот директора; пусть и—вектор смещения точек слоя, a v—снова изменение директора (n = n₀ + v). При длинноволно­вых деформациях слой можно рассматривать как геометрическую поверхность, и тогда малые величины v и и связаны друг с другом соотношением v = — grad (un₀) (изменение направления нормали к поверхности); для их фурье-компонент имеем: Vk = — гх(и_кп₀), где х —составляющая к в плоскости слоя. При наличии магнитного поля изменение направления директора вно­сит в AF_n дополнительный вклад (141,3), пропорциональный v². В свою очередь это приведет к тому, что в интеграле (137,9), определяющем средний квадрат флуктуационного смещения, в знаменателе подынтегрального выражения появится (наряду с членом <~ х⁴) еще и член ~ х²; в результате расходимость интеграла исчезнет.

Наконец, остановимся на вопросе о принципиальной возмож­ности существования жидкокристаллических двумерных систем (пленок). В такой системе ориентация молекул задается дирек­тором п, лежащим в плоскости пленки. Если рассмотреть его флуктуации (с волновыми векторами к, лежащими в плоскости пленки), то для них получится выражение, аналогичное (141,6): при отсутствии поля <Vk> 1/ф(k_x, k_y), где q>(k_x, k_y) — квадра­тичная функция компонент вектора к. Но для нахождения пол­ной флуктуации <v²> это выражение должно быть теперь про­интегрировано по iPkrokdk, и интеграл логарифмически расхо­дится. Таким образом, тепловые флуктуации размывают жидкокри­сталлическую двумерную структуру. Как и в случае твердокри-сталлической двумерной структуры (§ 137), однако, логарифми­ческий характер расходимости не исключает возможности существования такой структуры в участках конечного размера.

ГЛАВА XIV

ФАЗОВЫЕ ПЕРЕХОДЫ ВТОРОГО РОДА И КРИТИЧЕСКИЕ ЯВЛЕНИЯ

§ 142. Фазовые переходы второго рода

В § 83 было уже указано, что переход между фазами раз­личной симметрии (кристалл и жидкость, различные кристал­лические модификации) не может совершаться непрерывным образом, подобно тому, как это возможно для жидкости и газа. В каждом состоянии тело обладает либо одной, либо другой симметрией, и потому всегда можно указать, к которой из обеих фаз оно относится.

Переход между различными кристаллическими модификациями совершается обычно путем фазового перехода, при котором про­исходит скачкообразная перестройка кристаллической решетки и состояние тела испытывает скачок. Однако наряду с такими скачкообразными переходами возможен и другой тип переходов, связанных с измене­нием симметрии.

Для выяснения природы этих переходов
обратимся к конкретному примеру. При
высоких температурах BaTi0₃ имеет куби-
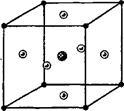
ческую решетку с ячейкой, изображенной
на рис. 60 (атомы Ва в вершинах, атомы
О в центрах граней и атомы Ti в центрах
•ffa, 90 ФП ячеек). При понижении температуры, при
Рис 60 некотором определенном ее значении, атомы

Ti и О начинают смещаться относительно атомов Ва в направлении одного из ребер куба. Ясно, что как только начинается это смещение, симметрия решетки сразу ме­няется, превращаясь из кубической в тетрагональную.

¹) Для упрощения рассуждений мы говорим условно о расположении атомов и о симметрии этого расположения, как если бы атомы были неподвижны. В действительности следовало бы говорить о распределении вероятностей раз­личных положений атомов в пространстве и о симметрии этого распределения.

Этот пример характерен тем, что никакого скачка в измене­нии состояния тела не происходит. Расположение атомов в кри­сталле ^х) меняется непрерывным образом. Однако уже сколь угодно малое смещение атомов от их первоначального симметричногорасположения достаточно для того, чтобы симметрия решетки сразу изменилась. Осуществляемый таким способом переход одной кристаллической модификации в другую называется фазовым переходом второго рода в противоположность обычным фазовым переходам, называемым в этой связи переходами первого рода

Таким образом, фазовый переход второго рода является не­прерывным в том смысле, что состояние тела меняется непре­рывным образом. Подчеркнем, однако, что симметрия в точке перехода меняется, разумеется, скачком, и в каждый момент можно указать, к которой из двух фаз относится тело. Но в то время, как в точке фазового перехода первого рода находятся в равновесии тела в двух различных состояниях, в точке пере­хода второго рода состояния обеих фаз совпадают.

Наряду со случаями, в которых изменение симметрии тела осуществляется посредством смещения атомов (как в приведен­ном выше примере), изменение симметрии при фазовом переходе второго рода может быть связано и с изменением упорядочен­ности кристалла. Как уже было указано в § 64, понятие об упорядоченности появляется, если число узлов решетки, в кото­рых могут находиться атомы данного рода, превышает число этих атомов. Будем называть места, на которых находятся атомы данного рода во вполне упорядоченном кристалле, «своими» в про­тивоположность «чужим», на которые атомы частично переходят при «разупорядочивании» кристалла. Во многих случаях, которые и будут интересовать нас в связи с вопросом о переходах вто­рого рода, оказывается, что свои и чужие узлы геометрически совершенно подобны и отличаются только тем, что для них раз­личны вероятности нахождения атомов данного рода²). Если теперь эти вероятности в своих и чужих местах сравняются (при этом, конечно, они не будут равны единице), то все эти узлы станут эквивалентными, а следовательно, появятся новые эле­менты симметрии, т. е. повысится симметрия решетки. Такой кристалл мы будем называть неупорядоченным.

²) Заметим, что в этом случае мы всегда можем считать, что вероятность нахождения атома в своем узле больше, чем в чужом, просто потому, что в противном случае мы могли бы назвать чужие узлы своими и наоборот.

Поясним сказанное примером. Вполне упорядоченный сплав CuZn имеет кубическую решетку с атомами Zn, расположенными, скажем, в вершинах, и атомами Си—в центрах кубических ячеек (рис. 61, а; решетка Бравэ—простая кубическая). При разупо-рядочении (при повышении температуры) атомы Си и Zn меня­ются местами, т. е. для всех узлов появляются отличные от нуля вероятности нахождения атомов обоего рода. До тех пор, пока вероятности нахождения атома Си (или Zn) в вершинах и цен­трах ячеек неодинаковы (не вполне упорядоченный кристалл), эти узлы остаются неэквивалентными и симметрия решетки ос­тается прежней. Но как только эти вероятности сравниваются, все узлы становятся эквивалентными и симметрия кристалла повышается — появляется новый трансляционный период (из вер­шины в центр ячейки), и кристалл приобретает объемноцентри-

х--------------.х рованную кубическую же решетку Бравэ

(рис. 61, б)¹).

Мы говорили выше лишь о переходах между различными кристаллическими моди­фикациями. Но фазовые переходы второго рода не обязательно должны быть связаны с изменением симметрии именно расположе­ния атомов в решетке. Путем перехода второго рода может осуществляться также и взаимное превращение двух фаз, отлича­ющихся каким-либо иным свойством сим­метрии. Таковы точки Кюри ферромагнитных или антиферромагнитных веществ; в этом случае мы имеем дело с изменением сим­метрии расположения элементарных магнит­ных моментов в теле (точнее, с исчезнове­нием токов j в нем — см. примечание на стр. 436). Фазовыми переходами второго рода являются также переход металла в сверх­проводящее состояние (в отсутствие магнитного поля) и переход жидкого гелия в сверхтекучее состояние. В обоих этих случаях состояние тела меняется непрерывным образом, но в точке пере­хода тело приобретает качественно новое свойство.

^х) В принципе возможны случаи, когда появление упорядоченности не при­водит к изменению симметрии кристалла. В таком случае фазовый переход второго рода невозможен: если бы даже переход упорядоченного кристалла в неупорядоченный произошел непрерывным образом, никакого скачка тепло­емкости (см. ниже) все равно не было бы (фазовый же переход первого рода возможен, конечно, и в этом случае). В литературе встречается утверждение о связи между фазовыми перехо­дами второго рода и появлением в кристалле вращающихся молекул (или ра­дикалов). Такой взгляд ошибочен, так как в точке перехода второго рода состояние тела должно меняться непрерывным образом, и потому не может возникнуть резкое изменение характера движения. Если речь идет о фазовом переходе, связанном с поворотами молекул в кристалле, то различие между обеими фазами должно заключаться в том, что в более симметричной фазе вероятности различных ориентации молекул одинаковы, а в менее симметрич­ной—различны.

Поскольку состояния обеих фаз в точке перехода второго рода совпадают, то ясно, что симметрия тела в самой точке перехода во всяком случае должна содержать все элементы сим­метрик обеих фаз. В дальнейшем будет показано, что симметрия в самой точке перехода совпадает с симметрией везде по одну сторону от этой точки, т. е. с симметрией одной из фаз. Таким образом, изменение симметрии тела при фазовом переходе второго рода обладает следующим весьма существенным общим свойст­вом: симметрия одной из фаз является более высокой, а симмет­рия другой фазы—более низкой по отношению друг к другу¹). Подчеркнем, что при фазовом переходе первого рода измене­ние симметрии тела не подчинено никаким ограничениям, и сим­метрии обеих фаз могут не иметь ничего общего друг с другом.

В огромном большинстве всех известных случаев фазовых переходов второго рода более симметричная фаза соответствует более высоким температурам, а менее симметричная — более низ­ким. В частности, переход второго рода из упорядоченного в не­упорядоченное состояние происходит всегда при повышении тем­пературы. Это правило, однако, не является термодинамическим законом и потому допускает исключения²).

Для краткости мы будем ниже условно называть более сим­метричную фазу просто симметричной, а менее симметричную — несимметричной.

Для количественной характеристики изменения структуры тела при прохождении через точку фазового перехода можно ввести величину л (которую будем называть параметром по­рядка), определенную таким образом, чтобы она пробегала отличные от нуля (положительные или отрицательные) значения в несимметричной фазе и была равна нулю в симметричной фазе. Так, для переходов, связанных со смещением атомов от их поло­жений в симметричной фазе, под т) можно понимать величину этого смещения. Для переходов, связанных с изменением упоря­доченности кристалла (например, в приведенном примере сплава CuZn), параметр ц может быть определен как

_ WCu — W_Zn ¹ WCa+WZn '

^г) Напомним, что мы называем более высокой симметрию, включающую в себя все элементы (повороты, отражения и трансляционные периоды) другой, более низкой, симметрии и, сверх того, еще дополнительные элементы. Указанное требование является необходимым, но еще отнюдь не достаточ­ным условием возможности фазового перехода второго рода; мы увидим ниже, что возможные изменения симметрии при таком переходе подчинены еще более далеко идущим ограничениям. ²) Такова, например, так называемая нижняя точка Кюри сегнетовой соли, ниже которой кристалл относится к ромбической, а выше—к моноклинной системе.

где о?си и w_Zn — вероятности нахождения в каком-либо узле атома Си или Zn. Для магнитных переходов под т) можно понимать макроскопический магнитный момент (отнесенный к единице объема) ферромагнетика или магнитный момент подре-шетки — в случае антиферромагнетика.

Подчеркнем лишний раз, что симметрия тела меняется (повы­шается) лишь в тот момент, когда т) обращается в точности в нуль; любое сколь угодно малое, но отличное от нуля значе­ние параметра порядка приводит уже к понижению симметрии. При прохождении через точку фазового перехода второго рода обращение tj в нуль происходит непрерывным образом, без скачка.

Отсутствие скачка состояния в точке фазового перехода вто­рого рода приводит к тому, что термодинамические функции состояния тела (его энтропия, энергия, объем и т. п.) остаются непрерывными при прохождении через точку перехода. Поэтому фазовый переход второго рода, в отличие от переходов первого рода, не сопровождается выделением или поглощением тепла. Мы увидим, однако, что производные от указанных термодина­мических величин (т. е. теплоемкость тела, коэффициент тепло­вого расширения, сжимаемость и т. п.) испытывают скачок в точке перехода второго рода.

Следует иметь в виду, что с математической точки зрения точка фазового перехода второго рода представляет собой некоторую особую точку его термодинамических величин, в част­ности термодинамического потенциала Ф (характер этой особен­ности будет обсужден в §§ 148, 149). Для того чтобы уяснить это обстоятельство, напомним предварительно, что точка фазо­вого перехода первого рода не представляет особенности: это есть точка, в которой термодинамические потенциалы обеих фаз Ф_Х(Я, Т) и Ф₂(Р, Т) равны друг другу, причем каждая из функций и Ф₂ по обе стороны точки перехода соответствует некоторому равновесному (хотя, возможно, и метастабильному) состоянию тела. При фазовом же переходе второго рода термо­динамический потенциал каждой из фаз, если его формально 'рассматривать по другую сторону точки перехода, вообще не соответствует какому бы то ни было равновесному состоянию, т. е. какому бы то ни было минимуму Ф (мы увидим в следую­щем параграфе, что термодинамический потенциал более симмет­ричной фазы по другую сторону точки перехода соответствовал бы даже максимуму Ф).

Дата добавления: 2014-11-07