Ol — V2X 34 страница

+

(149,8)

_An/v

Произведем дальнейшие рассуждения на основании формулы (149,7). Как уже отмечалось в связи с (148,18), при заданном отличном от нуля h термодинамические функции не имеют осо­бенности по г и потому должны быть разложимы по целым степеням этой переменной. Это значит, что при пфО, t—>0 функция ц>(х) в (149,7) разлагается в ряд по целым степеням малой переменной x=t/h^^v'. Первые члены этого разложения дают

Ф(г\ Л)с/эА^

где Cj, с_а — постоянные коэффициенты. Потребовав теперь, чтобы параметр порядка и теплоемкость, вычисленные как

__J_ao> _{г т} д*Ф

^ ^— V,67i ' р ~ ^с dt ^[40] '

вели себя при /—s-О по законам г)слЛ^1/6 и (отвечаю-

щим случаю сильного поля), получим два соотношения между критическими индексами:

Old —1)6=1, |*(|—d)=e;

легко проверить, что они действительно следуют из уже извест­ных нам соотношений, полученных ранее другим способом.

Пусть теперь t имеет отличное от нуля значение; тогда тер­модинамические величины не имеют особенности при прохожде-

^х) Напомним, однако, лишний раз, что в эффективном гамильтониане т] фигурирует как переменная, по которой производится континуальное интегри­рование в статистическом интеграле. В термодинамических же формулах под т| подразумевается равновесное значение параметра порядка, которое дается про­изводной дФ/dh (или dQ/dh) от термодинамического потенциала, определенного по статистическому интегралу. Симметрия эффективного гамильтониана приво­дит, конечно, к аналогичной симметрии в термодинамических соотношениях.

нии нулевого значения переменной Л, и потому функция Ф(г, Л) разложима по целым степеням А. Это значит, что при Л —*■ О, t Ф 0 разложение функции ф (х) по малой переменной l/x = h^^/v/t должно иметь вид

Ф(л:)слх^[1 +c₁x-^v^+c₂x-^+...];

множитель x^vd компенсирует нецелую степень а перемен­ная разложения х-^слА. Разложение, однако, различно при t > 0 и при t < 0. При / > 0 потенциал Ф (t, Л) содержит только четные степени Л, поскольку производная —d<S/dh = Vr\ должна быть (в симметричной фазе) нечетной функцией Л:

1 + С,­

г>0, (149,9)

При Л—>-0 теплоемкость должна вести себя по закону t~^a, а параметр порядка — по закону r\ = yh^ht~^ (отвечающим случаю слабого поля); легко убедиться, что получающиеся отсюда соотношения тоже эквивалентны уже известным. Если же температура t < 0, то разложение Ф(г, А) при А—>-0 содер­жит все целые степени А:

vd

Фсл(— t)

(149,10)

(с другими, конечно, коэффициентами с₁₍ с₂)^г). Легко проверить, что для параметра спонтанного (не зависящего от А) порядка получается требуемый закон (—/)Р.

О преобразовании корреляционного радиуса шла речь выше. Осталось рассмотреть корреляционную функцию флуктуации параметра т) при t—+0 и потребовать масштабной инвариант­ности выражения

G(r) = const-r-<^d-²⁺£> (/ = 0).

При этом следует считать, что флуктуирующие величины п(г) в разных точках пространства преобразуются независимо таким же образом, как и среднее значение т)^а). Тогда корреляционная функция преобразуется как G—>-Ga^2Ai, и мы получим условие

d + 2-4=S- <149,11)

И это равенство является следствием уже известных.

Остановимся в заключение на численных значениях крити­ческих показателей. Экспериментальные данные и результаты численных расчетов свидетельствуют о том, что (в трехмерном случае) индексы а и £ довольно малы: а~0,1, £~0,05. В пер­вой строке следующей ниже таблицы даны значения остальных индексов, получающиеся, если положить а = £ = 0 (d = 3). Во второй строке приведены значения, получающиеся, если при­нять для а и £ их оценку по упомянутому в § 147 методу Вильсона (для переходов, описывающихся эффективным гамиль­тонианом (147,6) с одним параметром порядка¹)):

а & у б е ц v £

С149 12)

О 1/3 4/3 5 0 2/5 2/3 О V^1-".¹^

0,08 0,33 1,26 4,8 0,05 0,40 0,64 0,04

§ 150. Изолированные и критические точки непрерывного перехода

Разделяя фазы разной симметрии, кривая (на диаграмме Р, Т)
фазовых переходов второго рода не может, конечно, просто
i окончиться в некоторой точке. Она может,

/ однако, перейти в кривую фазовых перехо-
у дов первого рода. Точку, в которой одна
К/ кривая переходит в другую, можно назвать

/

критической точкой переходов второго рода; она в известном смысле аналогична обычной критической точке (точка К на рис. 66; на этом и следующих рисунках в этом пара-

*г графе сплошные и пунктирные линии изо-

Рис. 66. бражают кривые точек фазовых переходов

соответственно первого и второго родов)²). В рамках теории Ландау свойства вещества вблизи такой точки могут быть исследованы тем же развитым в § 143 мето­дом разложения по степеням параметра порядка (Л. Д. Лан­дау, 1935).

В разложении (143,3) критическая точка определяется обра­щением в нуль обоих коэффициентов А(Р, Т) и В(Р, Т) (до тех

пор, пока Л = 0, В > 0, мы имеем дело с переходом второго рода, так что кривая этих переходов заканчивается лишь там, где В изменит знак). Для устойчивости состояния тела в самой критической точке необходимо тождественное исчезновение члена пятого порядка*) и положительность члена шестого порядка. Таким образом, исходим из разложения

Ф(Р, Т, т)) = Ф₀(Л Т) + А(Р, T)rf + B(P, T)rf + D(P, Т)ц\

(150,1)

причем в критической точке Л_кр = 0, В_кр = 0, D_Kp > 0.

В несимметричной фазе минимизация термодинамического потенциала дает

yf = ±[-B+VB*-3AD]. (150,2)

Для энтропии S =— дФ/дТ этой фазы имеем, опуская члены высших степеней по rp 5 = 5₀—ап², где а = дА/дТ. Дифферен­цируя еще раз, находим теплоемкость

С_р=—. ^Та " (150,3)

^р 2 у В² — 3AD ' v - /

где выписан лишь член, в котором знаменатель обращается в критической точке в нуль.

Введем температуру Г₀ = Г₀(Р), для которой В²—ЗЛО = 0; очевидно, что при Р = Р_Щ, Т_а совпадает с Т_кр. Первый член разложения В²—3AD по степеням Т—Т₀:

B* — 3AD = — 3a₀D₀(T—Т₀). (150,4)

Вблизи критической точки разность Т_С(Р)~Т₍₎{Р) является малой величиной второго порядка; действительно, при Т = Т_е(Р) имеем Л = 0, и потому разность

ТАР)-Т.(Р) = -^ (150,5)

т. е. стремится при Р—>-Р_кр к нулю как £^а. Подставив (150,4) в (150,3), находим

(с той же точностью коэффициент в этой формуле может быть взят при вместо Т₀). Таким образом, теплоемкость несим­метричной фазы возрастает при приближении к критической точке как (Т₀ — Т)-¹'*.

Для состояний на самой кривой переходов второго рода имеем, полагая в (150,3) Л = 0 (или подставляя (150,5) в (150,6)) получим

Т а²

_с,,₁₎₌₌^р_ _(150(7)

Обращаясь в нуль в критической точке, в ее окрестности вели­чина В пропорциональна Г—Г_кр (или P—P_KV).

Определим теперь теплоемкость несимметричной фазы на линии переходов первого рода, но снова вблизи критической точки. В точках этой линии находятся в равновесии друг с другом две различные фазы—симметричная и несимметричная. Значе­ние параметра г\ во второй из них определяется условием равно­весия Ф(т)) = Ф₀, причем одновременно должно быть дФ/дц = 0. Подстановка Ф из (150,1) приводит к уравнениям

А + Br)*+Drf = 0, А + 2Brf + ЗОп⁴ = 0,

откуда

ri² = -^j, (150,8)

а подстановка этого значения снова в уравнение Ф(г|) = Ф₀ дает

4Л£> = £². (150,9)

Это—уравнение линии переходов первого рода.

Теплоемкость несимметричной фазы на этой линии получа­ется просто подстановкой (150,9) в (150,3):

C$> = lh0*L. (150,10)

Сравнение с (150,7) показывает, что теплоемкость на линии переходов первого рода вдвое больше теплоемкости на линии переходов второго рода при том же расстоянии от критической точки. Теплота перехода из несимметричной в симметричную фазу:

q = T_Kp(S₀-S) = (^)^\B\. (150,11)

Покажем еще, что кривая переходов первого рода смыкается в критической точке с кривой переходов второго рода без излома. На первой кривой производная dT/dP определяется условием

2DdA + 2Л dD—B dB = 0,

получающимся дифференцированием уравнения (150,9). Уравне­ние же кривой переходов второго рода: Л = 0, так что dT/dP определяется условием dA = 0. Но в критической точке Л = 0,

В = 0 и оба условия совпадают, так что dT/dP не имеет скачка. Аналогичным образом можно убедиться в том, что вторая про­изводная d²T/dP* испытывает скачок.

Рис. 67.

Мы знаем уже, что теория Ландау, на которой основаны изложенные здесь выводы, неприменима вблизи линии перехо­дов второго рода. Интересно, однако, что условия примени­мости этой теории улучшаются по мере приближения к крити­ческой точке, что видно уже из неравенства (146,15), в правую часть которого входит как раз В. Разумеется, обращение В в нуль не означает, что флуктуационные поправки отсутствуют в критической точке вовсе. Оказывается, однако, что оно при­водит к исчезновению главных вблизи линии перехода (степен­ных) поправок. Остающиеся поправки имеют логарифмический

Рис. 68.

характер и приводят к тому, что результаты флуктуационной теории отличаются от результатов теории Ландау лишь степе­нями логарифма расстояния до критической точки. В частно­сти, dT/dP в критической точке по-прежнему непрерывна.

Далее остановимся (снова в рамках теории Ландау) на неко­торых свойствах точек пересечения линий фазовых переходов первого и второго рода.

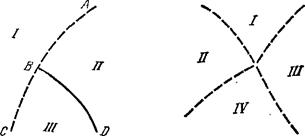
Симметрия несимметричной фазы при фазовом переходе вто­рого рода определяется (как было показано в § 145) миними­зацией членов четвертого порядка в разложении Ф как функций коэффициентов Yi ^{= T}li/'4- Но эти члены зависят также и от Р и Г, и поэтому может оказаться, что на разных участках линии переходов несимметричная фаза имеет различную симметрию. В простейшем случае такого рода мы имеем дело с пересече­нием линии переходов второго рода (кривая АС на рис. 67) с линией переходов первого рода (линия BD). Область /—сим­метричная фаза, а группы симметрии фаз II и /// — подгруппы группы симметрии фазы I. Они, однако, вообще говоря, не являются подгруппами друг друга, и потому разделяющая этифазы кривая BD—линия переходов первого рода. В точке В все три фазы тождественны^[41]).

На рис. 68 показан возможный тип пересечения нескольких линий переходов второго рода. Если / — наиболее симметрич­ная фаза, то группы симметрии фаз // и /// являются под­группами группы симметрии фазы /, группа же симметрии фазы IV—подгруппа одновременно групп симметрии фаз // и III*).

Рис. 69.

Наконец, осталось рассмотреть случай, когда члены третьего порядка в разложении термодинамического потенциала не обра­щаются в нуль тождественно. В этом случае условие существо­вания точки непрерывного фазового перехода требует обращения в нуль наряду с коэффициентом А (Р, Т) также и коэффициен­тов В_а(Р, Т) при инвариантах третьего порядка в разложе­нии (145,6). Очевидно, что это возможно, только если имеется всего один инвариант третьего порядка; в противном случае мы получили бы более двух уравнений для двух неизвестных Р и Т. При наличии всего одного инварианта третьего порядка два уравнения А (Р, Т) — 0 и В (Р, Т) — 0 определяют соответ­ствующие пары значений Р, Т, т. е. точки непрерывного фазо­вого перехода являются изолированными.

Будучи изолированными, эти точки должны лежать опреде­ленным образом на пересечении кривых (в плоскости Р, Т) фазовых переходов первого рода. Имея в виду, что такие изо­лированные точки непрерывного перехода еще не наблюдались на опыте, мы не станем производить здесь подробное исследо­вание, ограничившись лишь указанием результатов^[42]).

²) Точку пересечения типа рис. 67 называют в литературе бикршпической, а типа рис. 68—тетракритической.

Наиболее простой тип изображен на рис. 69, а. Фаза / обла­дает более высокой симметрией, а фазы // и /// — более низ-

кой; при этом симметрии фаз // и /// одинаковы, и эти фазы отличаются лишь знаком т). В точке непрерывного перехода (О на рис. 69) все три фазы становятся тождественными.

В более сложных случаях в точке непрерывного перехода касаются две (как на рис. 69, б) или более кривых фазовых переходов первого рода. Фаза / — наиболее симметричная, остальные—менее симметричны, причем симметрии фаз // и III (и фаз IV и V) одинаковы, и эти фазы отличаются лишь знаком г).

§ 151. Фазовый переход второго рода в двумерной решетке

Невозможность теоретического определения критических ин­дексов в общем виде придает особый интерес рассмотрению простой модели, допускающей точное аналитическое решение задачи о фазовом переходе второго рода. Это—определенная модель двумерной решетки, для которой задача о фазовом пере­ходе была впервые решена Онсагером (L. Onsager, 1944) [43]).

Рассматриваемая модель представляет собой плоскую квад­ратную решетку, состоящую из N узлов, в каждом из которых находится «диполь» с осью, перпендикулярной к плоскости решетки. Диполь может иметь две противоположные ориента­ции, так что общее число возможных конфигураций диполей в решетке равно 2^ ²). Для описания различных конфигураций поступим следующим образом. С каждым узлом решетки (с цело­численными координатами к, I) свяжем переменную а_к1, при­нимающую два значения ±1, соответствующие двум возможным ориентациям диполя. Если ограничиться только учетом взаимо­действия между соседними диполями, то энергия конфигурации может быть записана в виде

L

E(a)= — J 2 (tf[44]o-n+i + o-«o-ft+u) (151,1)

k, i=i

(L — число узлов в ребре решетки, которую представляем себе в виде большого квадрата; N — L^ia)). Параметр J определяет энергию взаимодействия пары соседних диполей, равную —/ и + J соответственно для одинаковых и противоположных ориентации диполей. Будем полагать; что J > 0. Тогда наимень­шей энергией обладает «полностью поляризованная» (упорядо­ченная) конфигурация, в которой все диполи ориентированы в одну сторону. Эта конфигурация осуществляется при абсо­лютном нуле, а с увеличением температуры степень упорядо­ченности убывает, обращаясь в нуль в точке перехода, когда обе ориентации каждого диполя становятся равновероятными.

Определение термодинамических величин требует вычисле­ния статистической суммы

_{z =} 2_e-_£(a>/7 ₌ 2exp {^{a_kla_kl+1 + o_kla_k+u)\, (151,2)

(С) (а, \ k,l)

взятой по всем 2^N возможным конфигурациям (мы обозначили 6= J IT). Заметим, что

ехр (Qa_kla_k4') = ch Q + о_k[a_k-г sh 0 = ch в (1 -\-о_к1а_кЧ' th 0),

в чем легко убедиться, разложив обе стороны равенства по степеням 0 и учитывая, что все а|_г=1. Поэтому выражение (151,2) можно переписать в виде

Z = (l— x*)~^NS, (151,3)

где

5 = 2 П (1+хо_к1в_к1+,)(1+хо_к1в_к+и) (151,4)

(о) к, 1=1

и введено обозначение x — thQ.

Под знаком суммы в (151,4) стоит полином по переменным х и а_к1. Поскольку каждый узел (k, I) связан с четырьмя сосе­дями, то каждое а_к1 может встретиться в полиноме в степенях от нулевой до четвертой. После суммирования по всем а_к1 = ±\ члены, содержащие нечетные степени a_kt, обратятся в нуль, так что ненулевой вклад дадут только члены, содержащие а_м в сте­пенях 0, 2 и 4. Поскольку а^ = а|_г = а|_г= 1, то каждый член полинома, содержащий все переменные а_к1 в четных степенях, даст вклад в сумму, пропорциональный полному числу конфи­гураций 2^N.

Каждому члену полинома можно однозначно поставить в со­ответствие совокупность линий («связей»), соединяющих некото­рые пары соседних узлов решетки. Так, изображенным на рис. 70 графикам соответствуют члены полинома:

а) ^a^al+^^+j^.j,

б) X^%o\fi%_+l< iO%_+li i-iO^ i-xO%_t;_₂oI_i, l-t,

в) x¹⁰aliol_+u го1₊₁, i_io|_₁₍ ^aLi, i-M-i. /-«•

Каждой линии графика сопоставляется множитель х, а каж­дому ее концу — множитель о_к1.

в)

Тот факт, что отличный от нуля вклад в статистическую сумму дают лишь члены полинома, содержащие все a_k[ в четных степенях, геометрически означает, что в каждом узле графика должны оканчиваться либо две, либо четыре связи. Другими словами, суммирование ведется только по замкнутым графи­кам, причем допускается самопересечение в узлах (как в узле (k, /—1) на рис. 70, б).

б)

ki к* 1,t

а)

М к+?,1

к-2, И ^[к-Ц -1 k,L-l k+l,t-7 Ц-2

Х-2,1-2 * t к

kl k+lL

•	• • к-1,1-1 к,	1-1
			к+1,1-1
•	•		•

■1,1-2 к,1-2

• - *----------- А • •

н-ц-з

Рис. 70.

Таким образом, сумма 5 может быть представлена в сле­дующем виде:

г

где g_r—число замкнутых графиков, составленных из (четного) числа г связей; при этом всякий многосвязный график (напри­мер, график рис. 70, в) считается за один.

Дальнейший расчет состоит из двух этапов: 1) сумма по графикам указанного вида преобразуется в сумму по всем воз­можным замкнутым петлям, 2) получающаяся сумма вычисляется путем сведения к задаче о «случайных блужданиях» точки по решетке.

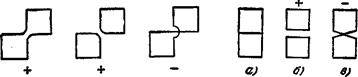
Будем рассматривать каждый график как совокупность одной или нескольких замкнутых петель. Для графиков без самопере­сечений такое представление самоочевидно; так, график рис. 70, в есть совокупность двух петель. Для графиков же с самопере­сечениями такое разбиение неоднозначно; одна и та же фигура может состоять из различного числа петель в зависимости от способа ее построения. Это иллюстрируется рис. 71, показы­вающим три способа представления графика рис. 70, б в виде одной или двух петель без самопересечений или в виде одной петли с самопересечением. Аналогичным образом может быть пройдено тремя способами каждое пересечение и на более сложных графиках.

Рис. 71.

Легко видеть, что сумму (151,5) можно распространить по всем возможным совокупностям петель, если при подсчете чисел графиков g_r каждый из них брать со знаком (—1)", где п—пол­ное число самопересечений в петлях данной совокупности. Дей­ствительно, при таком подсчете все лишние члены суммы авто­матически выпадают. Так, три графика рис. 71 войдут соответ­ственно со знаком +, +. —. так что два из них взаимно сократятся и останется, как и следовало, всего однократный вклад в сумму. В новой сумме будут фигурировать также гра­фики с «повторяющимися связями», простейший пример которых

Рис. 72.

изображен на рис. 72, а. Эти графики относятся к числу недо­пустимых (в некоторых узлах сходится нечетное число связей — три), но, как и следовало, из суммы они фактически выпадают: при построении соответствующих такому графику петель каж­дая общая связь может быть пройдена двумя способами—без пересечения (как на рис. 72, б) или с самопересечением (рис. 72, в), причем получающиеся совокупности петель войдут в сумму с противоположными знаками и взаимно сократятся. Далее можно избавиться от необходимости учитывать в явном виде число пересечений, если воспользоваться известным геометриче­ским фактом: полный угол поворота касательной при обходе плоской з!мкнутой петли равен 2я(/ +1), где /—целое (поло­жительное или отрицательное) число, четность которого сов­падает с четностью числа v самопересечений петли. Поэтому, если каждому узлу в петле (с углом поворота в нем <р = 0, ±я/2) сопоставить множитель eW*, то после обхода всей петли произведение этих множителей даст (—l)^v+1. Для совокупности же нескольких (s) петель мы получим в результате множитель (— \)^n+s, где n = 2]v.

Таким образом, можно не учитывать число пересечений, если брать каждый узел в петле с весом e^² и для всего графика (совокупность петель) ввести еще множитель (—\)^s (для пога­шения такого же множителя в (—\)^n+s).

Обозначим посредством f_r сумму по всем одиночным петлям длины г (т. е. состоящим из г связей), причем каждая петля входит с множителем е'^Чр/2 на каждый узел в ней. Тогда суммапо всем парам петель с общим числом связей г будет равна

г, + г_г=г

(множитель 1/2! учитывает, что при перестановке индексов г_х, г₂ получается одна и та же пара петель), и аналогично для троек и т. д. петель. Таким образом, сумма S принимает вид

5=0 Г,Г»,... = 1

Поскольку в S входят совокупности петель с любой общей длиной г₁ + г₂+..., то во внутренней сумме числа г,, г_а,... пробегают независимо все значения от 1 до оо *). Поэтому

г, r_s \г=1 /

и S приводится к виду

S = expf-2*7rY (151,6)

На этом заканчивается первый этап вычисления.

Для дальнейшего удобно связать с каждым узлом решетки четыре возможных направления выхода из нее, перенумеровав их специальным индексом v=l, 2, 3, 4, скажем по правилу

2 t

3+-. -+1

^J) Петли с числом узлов больше N все равно не дают вклада в сумму, так как непременно содержат повторяющиеся связи.

Введем вспомогательную величину W_r(k,l,v)—сумму по всем возможным переходам с длиной г из некоторого заданного исходного узла k₀, l₀, v₀ в узел k, I, v (каждая связь входит, как везде, с множителем е^{ч>^/2, где ф — изменение направления при переходе к следующей связи); при этом последний шаг, приводящий в узел k, I, v, не должен происходить со стороны, в которую направлена стрелка v^[45]). При таком определении W_r (k₀, l₀, v₀) есть сумма по всем петлям, выходящим из точки k₀, 1₀ в направлении v₀ и возвращающимся в эту же точку.

Очевидно, что

f' = h£ ^Wr(k₀,lo,v₀). (151,7)

Действительно, справа и слева стоит сумма по всем одиночным
петлям, но в каждая петля входит 2г раз, поскольку она

может проходиться в двух противоположных направлениях и относиться к каждому из своих г узлов в качестве исходного.

Из определения W_r(k, I, v) вытекают следующие рекуррент­ные соотношения:

W_r+1(k, I, l)=W_r(k-l, I, l) + e~~W_r(k,l-l,2) + 0 +

in

+ e~W_r(k, / + 1,4), W_r+1(k, I, 2)=e^W_r(k-\, I, \) + W_r(k, 2) +

+ e~~W_r(k + l, I, 3) + 0, (151,8)

in

W_r+1(k, /,3) = 0 + e* W_r(k,.l-l,2) + W_r(k + l,l,3) +

in

+ e~ * W_r(k,l + \,4),

in in

W_r+1(k, I, 4)='e" ⁴ W,(k-l,l, 1) + 0 + еЧР_г(*+1,/,3) +

+ W_r(k,l + l,4).

Способ составления этих соотношений очевиден; так, в точку k, I, 1 можно попасть, сделав последний (r+1-й) шаг слева, снизу или сверху, но не справа; коэффициенты при W_r возникают от множителей е''ч^>/'².

Обозначим посредством Л матрицу коэффициентов системы уравнений (151,8) (со всеми к, /), написанных в виде

W_r+1 (k, I, v) = 23 Л (klv I k'l'v') W_r (k^r, /', v').

k'l'V

Способ составления этих уравнений позволяет сопоставить этой матрице наглядный образ точки, «блуждающей» шаг за шагом по решетке с «вероятностью перехода» за один шаг из одного узла в другой, равной соответствующему элементу матрицы Л; фактически ее элементы отличны от нуля лишь для измене­ния k или / на 0 или +1, т. е. за каждый шаг точка прохо­дит лишь одну связь. Очевидно, что «вероятность перехода» длины г будет определяться матрицей А^г. В частности, диаго­нальные компоненты этой матрицы дают «вероятность» возвра­щения точки в исходный узел после прохождения петли длины г, т. е. совпадают с W_r(k₀, /₀, v₀). Поэтому

SpA' = 2 W_r(k₀,t₀, v₀).

*о'<Л'о

Сравнивая с (151,7), находим

I

где А,,-—собственные значения матрицы Л. Подставив это выра­жение в (151,6) и меняя порядок суммирования по i и по г, получим

S = ехр |-± £ £ 1 х'л|} = ехр {■!2 Ш (1 =

= ПКЬ⁼^. (151,9)

Матрица Л легко диагонализуется относительно индексов k, t путем перехода к другому представлению с помощью преоб­разования Фурье:

W_r(p,q,v) = 2 е" ^{" ⁺⁴⁾W_r(k,l,_V). (151,10)

ft, 1 = 0

После перехода в обеих сторонах уравнений (151,8) к компонен­там Фурье каждое из них будет содержать W_r (р, q, v) лишь с одинаковыми индексами р, q, т. е. матрица А диагональна по р, q. Для заданных р, q ее элементы равны

/ е-Р а-Ч-9 0 а&ч \

k{pqv\pqv') = \ _{0 a&}__{g вр а}__чА,

\а-Ч-Р 0 аеР еЯ J

где а = е'^я/4, e = e^2Iti/L.

Для заданных р, q простое вычисление дает

= Det (Sw—xAw') = (1 + х²)² —2х (1 — x») (cos ^ + cos.

Отсюда, согласно (151,3) и (151,9), находим окончательно ста­тистическую сумму:

L

Z = 2^(l—х²)-" П

р, <7=0

1/2

(1 + х²)²—2х(1 —х²) (cos ^-f-cos ^)

Термодинамический потенциал¹): Ф = — Т \nZ = —NTIn2 + NTIn<1 — х²) —

~Т^Т £^1п [(l+^)²-2x(l-x²)(cos^ + cos^-)]

2я NT

2 (2я)^!

или, переходя от суммирования к интегрированию ф = — NT In 2 + NT 1п(1— х²) —

In [(1+х²)² —2х (1 —х²) (cosMi+cos oi^da,dw₂ (151,12)

(напомним, что x = th(//T')).

Обратимся к исследованию этого выражения. Функция Ф(Т) имеет особую точку при том значении х, при котором аргумент логарифма под знаком интеграла может обратиться в нуль. Как функция от &_1У ю₂ этот аргумент минимален при cos = cos к>₂ = 1, когда он равен

(1 -fx²)² —4х(1—х²) = (х² + 2х—I)².

Это выражение имеет минимум, в котором оно обращается в нуль лишь при одном (положительном) значении x = x_c = V~2 — 1; соответствующая температура Т_с [ih ~ = х_с j и является точкой

фазового перехода.

Разложение Ф (/) по степеням t = T—Т_с вблизи точки пере­хода содержит наряду с регулярной частью также и особый член. Нас интересует здесь лишь последний (регулярную же часть заменим просто ее значением при /=0). Для выяснения его вида разлагаем аргумент логарифма в (151, 12) вблизи его минимума по степеням (a_lt ю_а и t, после чего интеграл прини­мает вид

Дата добавления: 2014-11-07