Ol — V2X 31 страница

С последним обстоятельством связана невозможность явлений перегрева или переохлаждения при фазовых переходах второго рода (которые возможны при обычных фазовых переходах). Каждая из фаз в этом случае вообще не может существовать по другую сторону от точки перехода (мы отвлекаемся, конечно, от времени установления равновесного распределения атомов, кото­рое в твердых кристаллах может оказаться значительным).

Задача

Пусть с—концентрация атомов одной из компонент бинарного твердого раст­вора, а с₀ — концентрация «своих» мест для этих атомов. Если с Ф с„, кристалл не может быть вполне упорядоченным. Предполагая разность с—с₀ малой и кристалл почти вполне упорядоченным, определить концентрацию X атомов на «чужих» местах, выразив ее через значение Х_а, которое она имела бы (для заданных Р и Т) при с = с₀ (С. Wagner, W. Schottky, 1930).

Решение. Рассматривая все время атомы только одной компоненты, вводим концентрацию X атомов на чужих местах и концентрацию X' своих мест, на которых не находится свой атом (концентрации определяются по отношению к полному числу всех атомов в кристалле). Очевидно, что

с—с₀ = Х—X'. (1)

Будем рассматривать весь кристалл как «раствор» атомов, находящихся на чужих местах, и узлов, на которых не находится свой атом, причем роль «растворителя» играют частицы, находящиеся на своих местах. Переход атомов с чужих мест на свои можно тогда рассматривать как «химическую реакцию» между «растворенными веществами» (с малыми концентрациями X и X') с образо­ванием «растворителя» (с концентрацией «I). Применив к этой «реакции» закон действующих масс, получим XX'= К, где К зависит лишь от Р я Т. При с = с₀ должно быть Я = £'=Я₀; поэтому К = Х%, так что

XX' = Я₀*. (2)

Из (1) и (2) находим искомые концентрации:

Х = 1 [(с~с₀)+ у_{с-с₀)*+4Х1], X' = у [- (с-с₀) + V(c-c₀)* + AXl].

§ 143. Скачок теплоемкости

Количественная теория фазовых переходов второго рода исхо­дит из рассмотрения термодинамических величин тела при задан­ных отклонениях от симметричного состояния (т. е. при задан­ных значениях параметра порядка rj); так, термодинамический потенциал тела представляется как функция от Р, Т и т|. При этом надо, конечно, иметь в виду, что в функции Ф(Р, Т, п) переменная т) в известном смысле не равноправна с перемен­ными Р и Т; в то время как давление и температура могут быть заданы произвольно, реально осуществляющееся значе­ние п само должно быть определено из условия теплового рав­новесия, т. е. из условия минимальности Ф (при заданных Р и Т).

Непрерывность изменения состояния при фазовом переходе второго рода математически выражается в том, что вблизи от точки перехода величина г) принимает сколь угодно малые зна­чения. Рассматривая окрестность точки перехода, разложим Ф(Р, Т, г)) в ряд по степеням гр

Ф(Р, Т, тО = Ф_й + ап + Лт]* + Сч³ + Вг1⁴ + ---, (143,1) где коэффициенты а, А, В, С,... являются функциями от Р и Т.

Необходимо, однако, подчеркнуть, что запись Ф в виде регу­лярного разложения (143,1) не учитывает упомянутого уже об­стоятельства, что точка перехода является особой для термоди­намического потенциала; то же самое относится и к производимому ниже разложению коэффициентов в (143,1) по степеням темпера­туры. Этот и следующие §§ 144—146 посвящены изложению тео­рии, основанной на допустимости таких разложений¹); вопрос об условиях ее применимости будет рассмотрен в § 146.

Можно показать (см. следующий параграф), что если состоя­ния с т| = 0 и г\фО отличаются своей симметрией (что и пред­полагается нами), то член первого порядка в разложении (143,1)

тождественно обращается в нуль: а = 0.
Что касается коэффициента А (Р, Т)
в члене второго порядка, то легко
видеть, что он должен обращаться в
нуль в самой точке перехода. Действи-
тельно, в симметричной фазе минимуму
Ф должно соответствовать значение
т| = 0; для этого, очевидно, необхо-
димо, чтобы было А > 0. Напротив, по
другую сторону точки перехода, в не-
симметричной фазе, устойчивому состоя-
р_ис 5₂_ нию (т. е. минимуму Ф) должны соот-

ветствовать отличные от нуля значения iy, это возможно лишь при А < 0 (на рис. 62 изображен вид функции Ф(п) при А < 0 и А > 0). Будучи положительным по одну сторону и отрицательным по другую сторону точки пере­хода, А должно, следовательно, обращаться в нуль в самой этой точке.

Но для того чтобы и самая точка перехода являлась устой­чивым состоянием, т. е. чтобы и в ней Ф как функция от ц имела минимум (при т) = 0), необходимо, чтобы в этой точке обратился в нуль также и член третьего порядка, а член чет­вертого порядка был положителен. Таким образом, должно быть:

А_с(Р,Т) = 0, С_С(Р, Т) = 0, В_с(Р,Т)>0, (143,2)

где индекс с отличает точку перехода. Будучи положительным в самой точке перехода, коэффициент В, разумеется, положи­телен и в ее окрестности.

Возможны два случая. Член третьего порядка может оказаться тождественно равным нулю в силу свойств симметрии тела: С (Р, Т) = 0. Тогда для точки перехода остается одно условие

^J) Эта теория принадлежит Л. Д. Ландау (1937). Им же была впервые указана общая связь фазовых переходов второго рода с изменением симмет­рии тела.

А(Р, Т) = 0; оно определяет Р и Т как функцию друг от друга. Таким образом, существует (в плоскости Р, Т) целая линия точек фазового перехода второго рода*).

Если же С не обращается тождественно в нуль, то точки перехода определяются из двух уравнений: А(Р, Т) — 0, С(Р, Т) = 0. В этом случае, следовательно, точки непрерывного фазового перехода могут быть лишь изолированными точками²).

Наиболее интересен, конечно, случай, когда имеется целая линия точек непрерывных переходов, и в дальнейшем мы будем подразумевать под фазовыми переходами второго рода только этот случай. Сюда относятся, в частности, переходы, связанные с появлением или исчезновением магнитной структуры. Это об­стоятельство является следствием симметрии по отношению к изменению знака времени. Термодинамический потенциал тела не может измениться при этом преобразовании, между тем как магнитный момент (играющий здесь роль параметра порядка) меняет знак. Ясно поэтому, что в таких случаях разложение Ф не содержит никаких вообще членов нечетных порядков.

Таким образом, будем считать, что С = 0, так что разложе­ние термодинамического потенциала имеет вид

Ф (Р, Т, г,) = Ф₀ (Р, Т) + А (Р, Т) ту² + В (Р, Т) rf\ (143,3)

Здесь В > 0, а коэффициент А > 0 в симметричной фазе и А < О в несимметричной фазе; точки перехода определяются уравне­нием А (Р, Г) = 0.

В излагаемой теории предполагается, что функция А (Р, Т) не имеет особенности в точке перехода, так что вблизи нее она разложима по целым степеням «расстояния» до этой точки.

А(Р,Т) = а(Р)(Т-Т_с), (143,4)

где Т_с — Т_с (Р)—температура перехода. Коэффициент же В (Р, Т) можно заменить на В(Р) = В(Р, Т_с). Таким образом, разложение термодинамического потенциала принимает вид

Ф(Р,Т) = Ф₀(Р, Т)+а(Р)(Т-Т_с)ч*+В(Р)ц\ (144,5)

причем В (Р) > 0.

²) Можно показать, что член третьего порядка в разложении во всяком случае существует, для перехода между изотропной жидкостью и твердым кри­сталлом. См. Л. Д. Ландау, ЖЭТФ 7, 627 (1937) (Собрание трудов, том II, статья 29, «Наука», 1969).

Зависимость г) от температуры вблизи точки перехода в не­симметричной фазе определяется из условия минимальности Ф как функции от т]. Приравнивая нулю производную дФ/дц, по­лучим: п (А -f- 2Вт]²) = 0, откуда

4ⁱ=-4=if<⁷>-^t> <¹⁴³*⁶>

(корень же т| = 0 отвечает при А < 0 не минимуму, а макси­муму Ф). Отметим, что расположение двух фаз по температурной шкале зависит от знака а: при а > О несиметричной фазе отве­чают температуры Т <Т_С, а при а < 0—температуры Т > 7V). Пренебрегая высшими степенями п, находим для энтропии

^Л~ дТ оТ ¹¹

(член с производной от rj по температуре выпадает в силу того, что дФ/дц = 0). В симметричной фазе т) = 0 и S*=S₀; в несим­метричной же

S = S₀+-^-(T-T_c). (143,7)

В самой точке перехода это выражение сводится к S₀, так что энтропия остается, как и следовало, непрерывной.

Наконец, определим теплоемкость С_р = Т (dS/dT)_P обеих фаз в точке перехода. Для несимметричной фазы имеем, дифферен­цируя (143,7),

С„ = С_р9+^. (143,8)

Для симметричной же фазы S — S„ и потому С_р = С_р9. Таким образом, в точке фазового перехода второго рода теплоемкость испытывает скачок. Поскольку В > О, то в точке перехода С_Р>С_ря, т. е. теплоемкость возрастает при переходе от симмет­ричной фазы к несимметричной (вне зависимости от их располо­жения по температурной шкале).

Наряду с С_р испытывают скачки также и другие величины: C_v, коэффициент теплового расширения, сжимаемость и т. п. Не представляет труда выразить скачки всех этих величин друг через друга. Исходим из того, что объем и энтропия в точке перехода непрерывны, т. е. их скачки AV и AS равны нулю:

АУ=0, AS = 0.

*) В дальнейшем мы будем для определенности везде считать, что симмет­ричная фаза расположена при Т > Т_с, как это и бывает в подавляющем боль­шинстве случаев. Соответственно будем считать, что а > 0.

Продифференцируем эти равенства по температуре вдоль кривой точек перехода, т. е. считая давление функцией от температуры,

Задача

Найти связь между скачками теплоемкости и теплоты растворения при переходе второго рода в растворе (Я. М. Лифшиц, 1950).

Решение. Теплота растворения, отнесенная к одной молекуле растворяе­мого вещества, определяется как

dW

где W — тепловая функция раствора, a w'^—тепловая функция на одну частицу чистого растворяемого вещества. Поскольку w'₀ не имеет отношения к фазовому переходу в растворе, имеем для скачка q

Л,=Л^=Л•(•_r">_-rA_:'^,»

дп дп \ дТ) дпдТ

(мы учли здесь, что химический потенциал ft' = дФ/дп непрерывен при переходе). С другой стороны, дифференцируя уравнение Д (дФ/дТ) = 0 (непрерывность энтро­пии) вдоль кривой зависимости температуры перехода от концентрации с (при постоянном давлении), найдем

dc дТ²^дпдТ Отсюда искомое соотношение:

Отметим, что при его выводе мы не делали никаких предположений о степени концентрированности раствора.

§ 144. Влияние внешнего поля на фазовый переход

Рассмотрим теперь, как меняются свойства фазового перехода при наложении на тело внешнего поля, действие которого зависит от величины параметра г). Не уточняя физической природы этого поля, сформулируем в общем виде предположения, делае­мые относительно его характера. Они сводятся к утверждению, что наложение такого поля описывается появлением в гамиль­тониане тела возмущающего оператора вида

Н_н = -фУ, (144,1)

*) Так, для ферромагнетика (вблизи его точки Кюри—точки перехода в парамагнитную фазу) параметром г\ являются макроскопический магнитный момент (отнесенный к единице объема), а полем А — магнитное поле; для сегнето-электрика параметр ц есть электрический дипольный момент единицы объема тела, a h—электрическое поле. В других случаях поле h может и не иметь прямого физического смысла, но его формальное введение помогает более глу­бокому уяснению свойств фазового перехода.

линейного по «напряженности» поля h и по оператору и вели­чины т); V—объем тела¹). Если термодинамический потенциал определен как функция Р, Т и h, то среднее (равновесное)

значение t| дается формулой

(согласно теореме о дифференцировании по параметру—ср. (11,4), (15,11)).

Чтобы обеспечить выполнение этого соотношения в теории Ландау, надо добавить к разложению (143,5) член вида —t\hV:

Ф(Р, Т, у]) = Ф₀(Р, Т) + att)² +Вц* — r\hV, (144,3)

где введено обозначение t = T — Т_С(Р)¹).

Отметим прежде всего, что уже сколь угодно слабое поле приводит к тому, что параметр т\ становится отличным от нуля во всей области температур. Другими словами, поле понижает симметрию более симметричной фазы, так что разница между обеими фазами исчезает. Соответственно исчезает также и диск­ретная точка фазового перехода; переход «размывается». В част­ности, вместо резкого скачка теплоемкости возникает аномалия, растянутая по некоторому температурному интервалу. Порядок величины этого интервала можно оценить из требования: i\hV ~ atrf; взяв г\ из (143,6), найдем отсюда

t~h²/*^{B V}. а

Для количественного исследования перехода пишем условие равновесия (дФ/дц)_т<й = 0²):

2atT\ + 4Br\³ = hV. (144,4)

Зависимость п от поля h имеет различный характер при тем­пературах выше и ниже Т_с³).

При />0 левая сторона уравнения (144,4) — монотонно воз­растающая функция от г| (рис. 63, а). Поэтому уравнение имеет при каждом заданном значении h всего один (вещественный) корень, обращающийся в нуль при Л = 0. Фунция т) (п) одно­значна, причем знак т| совпадает со знаком h (рис. 64, а).

²) Рассматриваем везде переходы при заданном давлении; индекс Р, указы- вающий постоянство давления при дифференцированиях, для краткости опускаем. ³) Напомним, что мы условились считать, что а > О, так что симметричной фазе (ii=0 при й = 0) отвечают температуры t > 0 (Т > Т_с).

Если же t < О, то левая сторона уравнения (144,4) —не монотонная функция т| (рис. 63, б), в результате чего в определенном интервале значений h уравнение имеет три различ­ных вещественных корня, так что функция r\(h) становится не­однозначной, как это изображено на рис. 64, б. Границы этого интервала определяются, очевидно, условием

—- (2atr\ + 45r|³) = 2at + 12Яг|^а = О, и даются неравенствами — h_t < h < h_t, где

_h _, 2 y/i (a I <|)»/«

(144,5)

Легко, однако, видеть, что весь участок кривой ВВ', на ко­тором (дц/дп)_т < 0, отвечает термодинамически неустойчивым

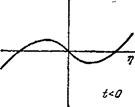
6>0

а)

Рис. 63.

состояниям. Действительно, дифференцируя уравнение (144,4) по п, находим

отсюда видно, что (д*Ф/дц²)_{т> h} < 0 при (дц!дК)_т < 0, т. е. Ф имеет здесь не минимум, а максимум.

На участках же АВ и А'В' термодинамический потенциал минимален, но величина этого минимума превышает минимумы, отвечающие соответственно участками A'D' и AD; в этом легко убедиться прямым вычислением, но результат и заранее очеви­ден: поскольку поле h входит в Ф в виде члена —rj/гК, то термодинамически заведомо выгоднее, чтобы знак т) совпадал со знаком h. Другими словами, участки АВ и А'В' отвечают метастабильным состояниям тела. Таким образом, истинный равновесный ход функции r\(h) дается сплошной линией DAA'D' на рис. 64, б, все точки которой отвечают термодинамически устойчивым состояниям. Если при заданной температуре / < О менять поле, то при прохождении им значения h = 0 возникает фазовый переход первого рода: в этой точке находятся в равновесии друг с другом фазы с противоположными по знаку значениями т] = ±(а|г|/25)¹/².

(144,7)

Определим восприимчивость тела как производную

^л \dh J Т; h-* О

Дифференцируя равенство (144,4), находим

дг\_ V

dh ~2at + 12Яп² '

и подставив сюда (при h—+0) tj² = 0 для / >0 или т)²——at/25 для t < 0, получим

_х=2^при/>0, _X=_L_ при /<0. (144,8)

Обращение _х в бесконечность при / ■—>■ О является естественным следствием упомянутой уже (в конце предыдущего параграфа)

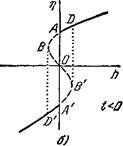
а)

Рис. 64.

все большей пологости минимума функции Ф(г)) при приближе­нии к точке перехода; ввиду этой пологости уже небольшое возмущение сильно меняет равновесное значение г\. Величина

(а И 1)

3/2

VB¹'*

дает значение поля, при котором индуцированный полем пара­метр "Пинд — Х^¹ становится того же порядка, что и характерная величина спонтанного (без поля) т|_сп ~ (а | / |/В)^1/2. Поля h<^h_t являются «слабыми» в том смысле, что в первом приближении не влияют на термодинамические величины тела. Поля же h^>h_t составляют область «сильных» полей, в которых значения термо­динамических величин в первом приближении определяются полем; при г = 0, очевидно, всякое поле является в этом смысле сильным.

В области сильных полей параметр порядка

n-(S)^W. <Н4,9₍

Легко проверить также, что в этом пределе теплоемкость С_р оказывается не зависящей от величины поля.

§ 145. Изменение симметрии при фазовом переходе второго рода

В изложенной в предыдущих параграфах теории мы рассмат­ривали фазовый переход второго рода с некоторым определен­ным изменением симметрии тела, заранее предполагая такой переход возможным. Такая теория, однако, не позволяет дать ответа на вопрос о том, может ли в действительности произойти данное изменение симметрии путем перехода второго рода. Этой цели служит развиваемая в этом параграфе теория, исходящая из другой постановки задачи: задана определенная симметрия тела в самой точке перехода, и требуется выяснить, какова может быть симметрия по обе стороны этой точки.

Будем говорить, для определенности, о фазовых переходах, связанных с изменением структуры кристаллической решетки, т. е. изменением симметрии расположения атомов в ней. Пусть р(х, у, г) есть (введенная в § 128) функция плотности, опреде­ляющая распределение вероятностей различных положений ато­мов в кристалле. Симметрия кристаллической решетки есть сово­купность (группа) таких преобразований координат, по отноше­нию к которым функция р (х, у, г) инвариантна. Мы подразумеваем здесь, разумеется, полную симметрию решетки, включающую в себя как повороты и отражения, так и бесконечный (дискрет­ный) набор всех возможных параллельных переносов (трансля­ций); другими словами, речь идет об одной из 230 пространст­венных групп.

Пусть G₀—группа симметрии, которой обладает кристалл в самой точке перехода. Как известно из теории групп, произ­вольную функцию р (х, у, z) можно представить в виде линей­ной комбинации некоторых функций ф_х, ф₂, обладающих тем свойством, что при всех преобразованиях данной группы они преобразуются друг через друга. В общем случае число этих функций равно числу элементов группы, но при определен­ной симметрии самой разлагаемой функции р число функций ф,-может быть и меньшим.

Имея в виду это обстоятельство, представим функцию плот­ности кристалла р (х, у, z) в виде суммы

Р = 2^Т№. i

где функции ф,- преобразуются друг через друга при всех пре­образованиях группы (?₀. Матрицы этих преобразований осу­ществляют некоторое представление группы (?₀. Выбор функций Ф,- не однозначен; вместо них самих можно взять, очевидно, любые их линейные комбинации. Как известно, можно всегда выбрать функции ф,- таким образом, чтобы они распались на ряд совокупностей, содержащих по возможности малое число функций, причем функции, входящие в состав каждой из них, при всех преобразованиях группы О₀ преобразуются только друг через друга. Матрицы преобразований функций, входящих в каждую из этих совокупностей, представляют собой неприво­димые представления группы О₀, а сами эти функции являются базисом этих представлений. Таким образом, можно написать:

Р = 22«^п>> (145,1)

п i

где я есть номер неприводимого представления, a i—номер функции в ее базисе. В дальнейшем мы будем считать функции Ф^"» некоторым определенным образом нормированными.

Среди функций ф;^п> всегда есть такая, которая сама по себе инвариантна по отношению ко всем преобразованиям группы G₀ (она осуществляет единичное представление группы). Другими словами, эта функция (которую мы обозначим как р₀) обладает симметрией О₀. Обозначая остальную часть р как бр, мы можем написать:

р = р₀ + бр. 6р = 2'2лг^я,фГ, (145,2)

где теперь из суммирования исключено единичное представление (это обстоятельство отмечено штрихом у знака суммы). Функция бр обладает симметрией более низкой, чем симметрия G₀, так как если бр и остается инвариантной при некоторых преобра­зованиях этой группы, то во всяком случае не при всех. Заме­тим, что симметрия G функции р (совпадающая, очевидно, с симметрией бр) предполагалась, собственно говоря, с самого начала более низкой, чем симметрия (?₀: в противном случае во всей сумме (145,1) стоял бы всего один член — сама функ­ция р, осуществляющая единичное представление¹).

Поскольку физическая величина бр вещественна и должна оставаться таковой при всех преобразованиях, то ясно, что говоря о неприводимых представлениях, мы должны подразуме­вать физически неприводимые представления, функции базиса ко­торых могут быть выбраны вещественными (§ 135); соответственно этому функции ф;"* везде ниже предполагаются вещественными.

^J) Для магнитных переходов вместо плотности р (х, у, z) надо было бы рассматривать плотность токов j (х, у, г) в теле. В парамагнитной фазе j = О, а по другую сторону точки перехода 6j=j мало.

Термодинамический потенциал Ф кристалла с функцией плот­ности р из (145,2) есть функция температуры, давления и коэф­фициентов г|[^л) (и зависит, естественно, от конкретного вида самих функций (plⁿ⁾). Реально осуществляющиеся значения r|{-ⁿ> как функций от Р и Т определяются термодинамически из условий равновесия, т. е. условий минимальности Ф. Тем самым определится и симметрия О кристалла, так как ясно, что сим­метрия функции (145,2) с функциями ср,-^Л), законы преобразова­ния которых известны, определяется значениями коэффициентов в линейной комбинации последних.

Для того чтобы в самой точке перехода кристалл имел симметрию G₀, необходимо, чтобы в этой точке обратились в нуль все величины nj"', т. е. чтобы было бр = 0, р = р₀. По­скольку изменение состояния кристалла при фазовом переходе второго рода непрерывно, то обращение бр в нуль в точке перехода должно произойти непрерывным образом, а не скач­ком, т. е. коэффициенты т\\^т должны обратиться в нуль, при­нимая вблизи точки перехода сколь угодно малые значения. Соответственно этому разложим потенциал Ф (Р, Т, ^,njⁿ⁾) вблизи точки перехода в ряд по степеням т|[-"'.

Предварительно заметим, что поскольку при преобразова­ниях группы Оо функции cpjⁿ⁾ преобразуются друг через друга (в пределах базиса каждого неприводимого представления), то можно представлять эти преобразования таким образом, как будто преобразуются (по тому же закону) не функции ср<-^И), а коэффициенты ц\^т. Далее, поскольку термодинамический потен­циал тела, очевидно, не может зависеть от выбора системы координат, то он должен быть инвариантным по отношению к любому преобразованию системы координат, в частности по отношению к преобразованиям группы О₀. Поэтому разложение Ф по степеням г)<^п) должно содержать в каждом члене только инвариантную комбинацию величин т|[-^П) соответствующей степени.

Из величин, преобразующихся согласно (не единичному) неприводимому представлению группы, нельзя составить линей­ный инвариант¹). Инвариант же второго порядка существует для каждого представления только один—положительно опре­деленная квадратичная форма из т)|^п), которую можно всегда привести к сумме квадратов.

Таким образом, начало разложения Ф имеет вид

Ф=Ф_в + 2'Л^(п>2г|{^я)*, (145,3)

л i

где Л^(в)—функции от Р и Т.

^г) Противное означало бы, что в данном представлении содержится единиЧ' ное, т. е. представление приводимо.

В самой точке перехода кристалл должен обладать симмет­рией Go, т. е. равновесию должны соответствовать значения ве­личин i\i^m = 0. Очевидно, что Ф может иметь минимум при всех ■nj"' = 0 только в том случае, если все А^{п) неотрицательны.

Если бы в точке перехода все A^w > 0, то они были бы поло­жительными и вблизи точки перехода, т. е. было бы все время ■nj"' = 0, и никакого изменения симметрии вообще не произошло бы. Для того чтобы появились отличные от нуля т)<-^П), необхо­димо, чтобы один из коэффициентов Aⁱⁿ⁾ изменил знак; в самой точке перехода, следовательно, этот коэффициент должен обра­титься в нуль^[1]). (Одновременное обращение в нуль двух коэф­фициентов А^{п) возможно только в изолированной точке в плоско­сти Р, Т. Такая точка является пересечением нескольких линий переходов второго рода.)

Таким образом, с одной стороны точки перехода все А^т > 0, а с другой стороны один из коэффициентов Л^(п> отрицателен. Соответственно этому с одной стороны от точки перехода всегда все г){^п) = 0, а с другой стороны появляются отличные от нуля г]'"'. Другими словами, мы переходим к результату, что с одной стороны от точки перехода кристалл обладает более высокой симметрией G₀, которая сохраняется и в самой точке перехода, а по другую сторону точки перехода симметрия понижается, так что группа G есть подгруппа группы Go-

В результате изменения знака одного из Л^(п) появляются отличные от нуля nj^n>, относящиеся к соответствующему п-му представлению. Таким образом, кристалл с симметрией g„ пере­ходит в кристалл с плотностью р = р„-_г-5р, где

6p = 2^>iⁿ⁾ (145,4)

с есть линейная комбинация функций базиса только одного (любого не единичного) из неприводимых представлений группы G₀. Соот­ветственно этому мы будем ниже опускать индекс п, указываю­щий номер представления, подразумевая всегда то из них, кото­рое как раз возникает при рассматриваемом переходе. Введем обозначения

Л²=2тЬ^?, ru=Wi (145,5)

^так что 2y?=lj и напишем разложение Ф в виде Ф = Ф₀(Р, Г) + Г|М(Р, T) + rf2C_a(P, T)f«>(y_t) +

а

+ г\^В_а(Р, Т)№(_У1)+..., (145,6)

а

где fa\ • • • —инварианты третьего, четвертого и т. д. поряд­ков, составленные из величин у,-; в суммах по а столько членов, сколько можно составить из у,- независимых инвариантов соот­ветствующего порядка. В этом разложении термодинамического потенциала в точке перехода должен обратиться в нуль коэф­фициент А. Для того чтобы сама точка перехода являлась устой­чивым состоянием (т. е. чтобы Ф обладало в этой точке мини­мумом при г), = 0), должны обратиться в нуль члены третьего порядка, а члены четвертого порядка должны быть существенно положительными. Как уже было указано в предыдущем пара­графе, линия (в плоскости Р, Т) фазовых переходов второго рода может существовать лишь при условии тождественного отсутствия членов третьего порядка в разложении Ф. Это условие можно сформулировать теперь как требование невозможности составле­ния инвариантов третьего порядка из величин т|,-, преобразую­щихся по данному неприводимому представлению группы Оо¹).

Предполагая это условие выполненным, напишем разложение с точностью до членов четвертого порядка в виде

Ф = Ф₀ + Л(Р, 7) _ч«+ ч*2я«(Р, Т)№(У,)- (145,7)

а

Поскольку член второго порядка не содержит у,-, то эти вели­чины определяются просто из условия минимальности членовчетвертого порядка, т. е. коэффициента при т]⁴ в (145,7) [2]). Обозна­чив соответствующее минимальное значение этого коэффициента просто как В(Р, Т) (оно должно быть, согласно сказанному выше, положительным), мы вернемся к разложению Ф в виде (143,3), и величина т) определится из условия минимальности Ф как функции только от т] так, как это было сделано в преды­дущем параграфе. Найденные таким образом значения величин у,-определяют симметрию функции

Дата добавления: 2014-11-07