Ol — V2X 27 страница

Займемся теперь рассмотрением всех возможных типов сим­метрии решеток Бравэ.

Предварительно докажем общую теорему, касающуюся сим­метрии кристаллических решеток по отношению к поворотам. Выясним, какими осями симметрии может обладать решетка. Пусть А (рис. 55) есть один из узлов решетки Бравэ, через который проходит (перпендикулярно к плоскости рисунка) ось симметрии. Если В — другой узел, отстоящий от А на один из трансляционных периодов, то через В должна проходить другая такая же ось симметрии.

Произведем теперь поворот вокруг оси, проходящей через А на угол ф = 2я/п (п — порядок оси). Тогда точка В вместе с про­ходящей через нее осью займет положение В'. Аналогично пово­рот вокруг В переводит точку А в А'. По условиям построения

точки А' и В' относятся к той же решетке Бравэ и потому могут быть совмещены друг с другом посредством параллельного переноса. Поэтому расстояние А'В' тоже должно быть трансля­ционным периодом решетки. Если а есть кратчайший период в данном направлении, то расстояние А'В' должно быть, следова­тельно, равно ар с целым р. Из рисунка мы видим, что это приводит к уравнению

или

Поскольку (cos ср |^1, то р может быть здесь равным 3, 2, 1, 0. Эти значения приводят соответственно к ц> = 2л/п с п = =2, 3, 4, 6. Таким образом, кристаллическая решетка может об­ладать осями симметрии только 2-го, 3-го, 4-го и 6-го порядков.

Перейдем теперь к изучению возможных типов симметрии
решетки Бравэ по отношению к поворотам и отражениям. Эти
типы симметрии носят название „,-,

кристаллических систем или син-гоний. Каждая из них представ­ляет собой определенную совокуп­ность осей и плоскостей симметрии, т. е. является одной из точечных

групп.

Легко видеть, что каждый Рис. 55.

узел решетки Бравэ представляет

собой ее центр симметрии. Действительно, каждому атому в ре­шетке Бравэ соответствует другой атом, расположенный на одной прямой с данным узлом и первым атомом таким образом, что оба атома находятся на равных расстояниях от узла. Если центр симметрии является единственным (кроме трансляций) элементом симметрии решетки Бравэ, имеет место так называемая

1. Триклинная система. Эта система, наименее сим­метричная из всех, соответствует точечной группе С,-. Узлы три-клинной решетки Бравэ расположены в вершинах одинаковых параллелепипедов с произвольными длинами ребер и углами между ними; такой параллелепипед изображен на рис. 56. Ре­шетки Бравэ принято обозначать особыми символами; решетка триклинной системы обозначается как 1\.

2. Моноклинная система является следующей по сте­пени симметричности. Ее элементы симметрии—ось второго по­рядка и перпендикулярная к ней плоскость симметрии, т. е. эта система представляет собой точечную группу С_2Л. Это есть сим­метрия, которой обладает прямой параллелепипед с произвольным основанием. Решетка Бравэ этой системы может осущест­вляться двумя способами. В первом случае—так называемая простая моноклинная решетка Бравэ (Г_т)—узлы расположены в вершинах прямых (в направлении Ь) параллелепипедов с произ­вольным параллелограммом в качестве грани ас (рис. 56). Во

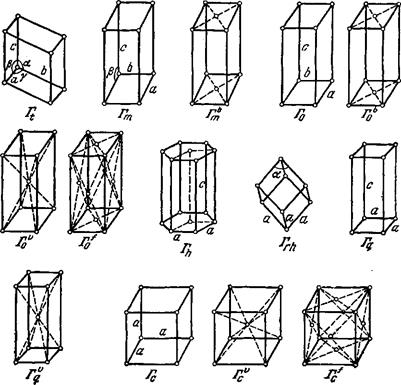
Рис. 56.

втором случае—решетка с центрированными основаниями (Г£,) — узлы расположены не только в вершинах, но и в центрах про­тивоположных прямоугольных граней параллелепипедов.

3. Ромбическая (или ортогональная) система соответствует точечной группе D_2h. Это есть симметрия прямо­угольного параллелепипеда с произвольными длинами ребер. К ромбической системе относятся четыре вида решеток Бравэ. В простой ромбической решетке (Г₀) узлы расположены в вер­шинах прямоугольных параллелепипедов. В решетке с центри­рованными основаниями (Го) узлы находятся также в центрах двух противоположных граней каждого параллелепипеда. Далее, в объемноцентрированной решетке (Г?) узлы находятся в верши­нах и центрах параллелепипедов и, наконец, в гранецентриро-ванной решетке (Г₀) узлы находятся, кроме вершин, также и в центрах всех граней.

4. Тетрагональная (или квадратная) система
представляет собой точечную группу D_ih; это есть симметрия,
которой обладает прямая призма с квадратным основанием.
Решетки Бравэ этой системы могут осуществляться двумя спо-
собами. Именно, существуют простая и объемноцентрированная
тетрагональные решетки Бравэ (обозначаемые соответственно

как Г, и Ц) с узлами, расположенными р------------------------ ^-------- ^

соответственно по вершинам и по вер- / \ / \ / \
шинам и центрам прямых призм с квад- / \/ \/ ^
ратными основаниями. л л /\ г

5. Ромбоэдрическая (или три- \ / ^ J ^ч_ч /_г
тональная) система соответствует ^л
точечной группе D_sd; такой симметрией

обладает ромбоэдр (фигура, получающаяся__________________

при растяжении или сжатии куба вдоль /\

его пространственной диагонали). В един- /^х \ / ^х\ / * \

ственной возможной в этой системе ре- <£-—-------------------------- ^-------

шетке Бравэ (Г_гЛ) узлы расположены в \ _/ \ /_х\
вершинах ромбоэдров. ^ч./ \/ \ ■

6. Гексагональная система °~—---------------------- °

соответствует точечной группе D_en; такой р_Ис. 57.

симметрией обладает правильная шести­гранная призма. Решетка Бравэ этой системы (Г_Л) может быть осуществлена только одним способом—ее узлы расположены в вершинах правильных шестигранных призм и в центрах их шести­угольных оснований. Полезно указать на следующее различие между ромбоэдрической и гексагональной решетками Бравэ. И в той и в другой узлы расположены в плоскостях, перпенди­кулярных к оси 6-го (или 3-го) порядка, таким образом, что образуют сетку из равносторонних треугольников. Но в гекса­гональной решетке в последовательных (вдоль оси С₆) таких плоскостях узлы расположены непосредственно друг над другом (на рис. 57 эти плоскости изображены в плане). В ромбоэдри­ческой же решетке в каждой следующей плоскости узлы распо­ложены над центрами треугольников, образованных узлами пре­дыдущей плоскости (кружки и крестики на рис. 57).

7. Кубическая система соответствует точечной группе
0_Л; это есть симметрия куба. К этой системе относятся три типа
решеток Бравэ: простая кубическая (Г_с), объемноцентрированная
(Г°) и гранецентрированная (Г£).

В последовательности систем триклинной, моноклинной, ром­бической, тетрагональной и кубической каждая обладает большей симметрией, чем все предыдущие. Другими словами, каждая следующая из них содержит в себе все элементы симметрии, содержащиеся в предыдущих. Ромбоэдрическая система обладает в том же смысле симметрией более высокой, чем моноклинная, и в то же время более низкой, чем симметрия кубической и гек­сагональной систем: ее элементы симметрии содержатся и в той и в другой. Наиболее симметричными являются именно эти две последние системы.

Рис. 58.

Укажем еще на следующее обстоятельство. На первый взгляд могло бы показаться, что возможны еще некоторые типы решеток Бравэ, кроме перечисленных четырнадцати. Так, если к простой тетрагональной решет­ке присоединить еще по узлу в центрах

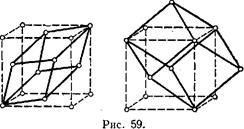
противоположных квадратных оснований призм, то решетка имела бы при этом по-прежнему тетрагональную симметрию. Легко, однако, видеть, что мы при этом не получили бы новой решетки Бравэ. Действительно, соединив узлы такой решетки указанным на рис. 58 (пунктирными линиями) способом, мы увидим, что новая решетка является по-прежнему простой тет­рагональной. Легко убедиться, что то же самое имеет место и во всех других подобных случаях.

Параллелепипеды решетки Бравэ, изображенные на рис. 56, сами по себе обладают всеми элементами симметрии той системы, к которой они относятся. Необходимо, однако, иметь в виду, что во всех случаях, за исключением только простых решеток Бравэ, эти параллелепипеды не являются элементарными ячей­ками: периоды, на которых они построены, не являются основ­ными. В качестве основных периодов в гранецентрированных решетках Бравэ можно выбрать векторы из какой-нибудь вер­шины параллелепипеда к центрам граней; в объемноцентриро-ванной — из вершины в центры параллелепипедов и т.п. На рис. 59 изображены элементарные ячейки для кубических реше­ток Г| и Г°; эти ячейки представляют собой ромбоэдры и отнюдь не обладают сами по себе всеми элементами симметрии куби­ческой системы. Очевидно, что объем v_f гранецентрированного параллелепипеда Бравэ в 4 раза больше объема элементарной ячейки: р_/=4и; объемы же объемноцентрированного параллеле­пипеда и параллелепипеда с центрированными основаниями равны удвоенным объемам элементарной ячейки: v_v = 2v, v_b = 2v.

Для того чтобы полностью определить триклинную решетку Бравэ, необходимо указать шесть величин: длины ребер ее параллелепипедов и углы между ними; в моноклинной доста­точно уже четырех величин, так как два из углов между реб­рами всегда прямые, и т. д. Аналогичным образом легко найти, что решетки Бравэ различных систем определяются следующим числом величин (длин ребер параллелепипедов или углов между ними):

Триклинная................... 6 Ромбоэдрическая.. 2

Моноклинная.... 4 Гексагональная... 2

Ромбическая.... 3 Кубическая....................... 1

Тетрагональная... 2

§ 131. Кристаллические классы

В целом ряде явлений, которые можно назвать макроскопи­ческими, кристалл ведет себя как однородное сплошное тело. Макроскопические свойства кристалла зависят только от направ­ления в нем. Так, особенности прохождения света через кристалл зависят только от направления луча света; тепловое расширение кристалла происходит, вообще говоря, различно по разным направлениям; наконец, упругие деформации кристалла под влиянием тех или иных внешних сил также зависят от направ­лений.

С другой стороны, симметрия кристаллов приводит к экви­валентности различных направлении в нем. Вдоль этих эквива­лентных направлений все макроскопические свойства кристалла будут в точности одинаковыми. Мы можем, следовательно, ска­зать, что макроскопические свойства кристалла определяются симметрией направлений в нем. Если, например, кристалл обла­дает центром симметрии, то всякому направлению в нем будет эквивалентно прямо противоположное.

Трансляционная симметрия решетки не приводит к эквива­лентности каких-либо направлений —параллельные переносы вообще не меняют направлений. По этой же причине для сим­метрии направлений несущественно различие между винтовыми и простыми осями симметрии или между простыми плоскостями симметрии и плоскостями зеркального скольжения.

Таким образом, симметрия направлений, а потому и макро­скопических свойств кристалла определяется совокупностью его осей и плоскостей симметрии, причем винтовые оси и плос­кости скольжения надо рассматривать как простые оси и плоскости. Такие совокупности элементов симметрии называ­ются кристаллическими классами.

Как мы уже знаем, реальный кристалл можно рассматри­вать как совокупность нескольких решеток Бравэ одинакового типа, вдвинутых друг в друга. Благодаря такому наложению решеток Бравэ симметрия реального кристалла, вообще говоря, отличается от симметрии соответствующей решетки Бравэ.

В частности, совокупность элементов симметрии класса дан­ного кристалла отличается, вообще говоря, от его системы. Очевидно, что присоединение к решетке Бравэ новых узлов может привести только к исчезновению некоторых из осей или плоскостей симметрии, но не к появлению новых. Поэтому кристаллический класс содержит меньше—или в крайнем случае столько же — элементов симметрии, чем соответствующая ему система, т. е. совокупность осей и плоскостей симметрии решетки Бравэ данного кристалла.

Из сказанного вытекает способ нахождения всех классов, относящихся к данной системе. Для этого надо найти все точечные группы, содержащие все или только некоторые из элементов симметрии системы. При этом, однако, может ока­заться, что какая-либо из получающихся таким образом точеч­ных групп состоит из элементов симметрии, содержащихся не только в одной, но в нескольких системах. Так, мы видели в предыдущем параграфе, что центром симметрии обладают все решетки Бравэ. Поэтому точечная группа С,- содержится во всех системах. Тем не менее распределение кристаллических классов по системам оказывается обычно с физической точки зрения однозначным. Именно, каждый класс должен быть отнесен к наименее симметричной из всех тех систем, в которых он со­держится. Так, класс С, должен быть отнесен к триклинной системе, не обладающей' никакими другими элементами симмет­рии, кроме центра инверсии. При таком способе распределения классов кристалл, обладающий некоторой решеткой Бравэ, ни­когда не будет относиться к классу, для осуществления кото­рого достаточной была бы решетка Бравэ более низкой системы (за одним только исключением—см. ниже).

Необходимость выполнения этого условия очевидна с физи­ческой точки зрения. Действительно, физически крайне неверо­ятно, чтобы атомы кристалла, относящиеся к его решетке Бравэ, расположились более симметричным образом, чем этого требует симметрия кристалла. Более того, если бы даже такое распо­ложение случайно осуществилось, то достаточно было бы любого, даже слабого, внешнего воздействия (скажем, нагревания), чтобы это расположение, как не связанное необходимым обра­зом с симметрией кристалла, нарушилось бы. Например, если бы кристалл, относящийся к классу, для осуществления кото­

рого была бы достаточна тетрагональная система, обладал ку­бической решеткой Бравэ, то уже незначительное воздействие оказалось бы способным удлинить или укоротить одно из ре­бер кубической ячейки, превратив ее в прямую призму с квад­ратным основанием.

Из этого примера видно, что существенную роль играет то обстоятельство, что решетка Бравэ высшей системы может быть переведена в решетку низшей системы уже посредством сколь угодно малой ее деформации. Есть, однако, одно исключение, когда такое превращение невозможно. Именно, гексагональная решетка Бравэ никакой бесконечно малой деформацией не мо­жет быть переведена в решетку более низкой по симметрии ромбоэдрической системы; действительно, из рис. 58 видно, что для превращения гексагональной решетки в ромбоэдричес­кую необходимо переместить узлы в чередующихся слоях на конечную величину — из вершин в центры треугольников. Это приводит к тому, что все классы ромбоэдрической системы осуществляются как с гексагональной, так и с ромбоэдрической решетками Бравэ¹).

Классы

Таким образом, для нахождения всех кристаллических клас­сов надо начать с отыскания точечных групп наименее сим­метричной системы—триклинной, переходя затем поочередно к системам более высокой симметрии и пропуская при этом те из содержащихся в них точечных групп, т.е. классов, которые уже были отнесены к низшим системам. Оказывается, что су­ществует всего 32 класса; приводим список этих классов, рас­пределенных по системам:

Триклинная Моноклинная Ромбическая

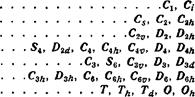
Тетрагональная Ромбоэдрическая Гексагональная Кубическая

Система

В каждом из написанных здесь рядов классов последний яв­ляется наиболее симметричным и содержит все элементы сим­метрии соответствующей системы. Классы, симметрия которых совпадает с симметрией системы, называются голоэдрическими. Классы, обладающие числом различных преобразований симмет­рии (поворотов и отражений, включая в их число тождественное

*) Кристаллы ромбоэдрических классов с гексагональной решеткой Бравэ принято относить к ромбоэдрической системе.

преобразование), вдвое и вчетверо меньшим, чем у голоэдериче-ского класса, называются соответственно геми- и тетартоэдри-ческими. Так, в кубической системе класс O_h является голоэдри­ческим, классы О, Т_А, Т_а — гемиэдрическими, а класс Т—тетар-тоэдрическим.

§ 132. Пространственные группы

Изучив симметрию решеток Бравэ и симметрию направлений в кристалле, мы можем, наконец, перейти к рассмотрению полной истинной симметрии кристаллических решеток. Эту симметрию можно назвать микроскопической в отличие от макроскопической симметрии кристаллов, рассмотренной в предыдущем параграфе. Микроскопическая симметрия определяет те свойства кристалла, которые зависят от расположения атомов в его решетке (таким свойством является, например, рассеяние рентгеновских лучей кристаллом).

Совокупность всех элементов симметрии (истинной) кристал­лической решетки называется ее пространственной группой. Ре­шетка всегда обладает определенной трансляционной симметрией и, кроме того, может обладать простыми и винтовыми осями симметрии, зеркально-поворотными осями и плоскостями симмет­рии— простыми и зеркального скольжения. Что касается тран­сляционной симметрии решетки, то она вполне определяется ее решеткой Бравэ, так как по самому определению последней кри­сталлическая решетка не может иметь никаких трансляционных периодов, кроме периодов ее решетки Бравэ. Поэтому для опре­деления пространственной группы кристалла достаточно, кроме указания решетки Бравэ, перечислить элементы симметрии свя­занные с поворотами и отражениями. При этом, конечно, должно быть указано также и расположение этих плоскостей и осей симметрии друг относительно друга. Далее надо иметь в виду, что трансляционная симметрия кристаллической решетки приво­дит к тому, что если решетка имеет какую-нибудь ось или пло­скость симметрии, то имеется бесконечное множество таких па­раллельных друг другу осей или плоскостей, совмещающихся друг с другом при параллельных переносах на трансляционные периоды решетки. Наконец, кроме этих осей (или плоскостей) симметрии, отделенных друг от друга периодами решетки, одно­временное наличие трансляционной симметрии и осей (плоскостей) симметрии приводит к появлению других осей (плоскостей), ко­торые не могут быть совмещены с первоначальными параллель­ным переносом на какой-нибудь период. Например, наличие плоскости симметрии приводит к появлению не только парал­лельных ей плоскостей, находящихся на расстоянии периода друг от друга, но еще плоскостей симметрии, делящих эти пе-

риоды пополам. Действительно, легко убедиться, в том, что от­ражение в некоторой плоскости с последующим переносом на какое-нибудь расстояние d в направлении, перпендикулярном к плоскости, эквивалентно простому отражению в плоскости, параллельной первоначальной и находящейся на расстоянии d/2 от нее.

Все возможные пространственные группы распределяются по кристаллическим классам. Именно, каждая пространственная группа относится к тому классу, в котором совокупность осей и плоскостей симметрии та же, что и в пространственной группе, если в последней не делать различия между простыми и винто­выми осями и простыми и скользящими плоскостями. Всего ока­зываются возможными 230 различных пространственных групп ¹). Они были впервые найдены Е. С. Федоровым (1895 г.). Прост­ранственные группы распределяются по классам следующим об­разом (табл. 1):

Таблица 1

Класс	Число групп	Класс	Число групп	Класс	Число групп	Класс	Число групп
Сг		Si		s*		Ctv
Ci		с4		Cav		De
Cs		Clll		D»		D«h
с,				D3d		T
		ClV		C»h		fh
CiV		Di		c.		Td
D2
		C3		D3h		On

Мы не станем приводить здесь перечисления элементов сим­метрии всех пространственных групп, которое было бы весьма громоздким. Его можно найти в специальных кристаллографиче­ских справочниках*).

*) Полное описание пространственных групп можно найти, например, в книге: Г. Я- Любарский, Теория групп и ее применения в физике (Приложение IV), Физматгиз, 1958 или в «Интернациональных таблицах для определения кри­сталлических структур» (International tables for X-ray crystallography, Kynoeh Press, Birmingham, 1952). В последних перечислены также для каждой прост­ранственной группы все эквивалентные точки.

Пространственные группы, не содержащие винтовых осей или плоскостей скольжения, называют симморфными; всего сущест­вует 73 такие группы. Остальные 157 пространственных групп содержат указанные элементы симметрии. Отметим, что кристал­лические решетки, относящиеся к несимморфным пространствен­ным группам, заведомо должны содержать по крайней мере два одинаковых атома в элементарной ячейке. Действительно, по­скольку поворот вокруг винтовой оси, или отражение в плоско­сти скольжения связаны с переносом на долю основного периода, то такое преобразование не совмещает друг с другом узлы ре­шетки Бравэ; кристаллическая решетка должна поэтому быть построена по крайней мере из двух вдвинутых друг в друга ре­шеток Бравэ, заполненных одинаковыми атомами.

§ 133. Обратная решетка

Все физические величины, характеризующие свойства кристал­лической решетки, обладают такой же периодичностью, как и сама решетка. Таковы, например, плотность заряда, создаваемая электронами атомов в решетке, вероятность нахождения атомов в том или ином месте решетки и т. п. Пусть функция U (г) пред­ставляет собой какую-либо из таких величин. Ее периодичность означает, что

L/(r-T-rt₁a₁-f-rt₂a₂ + rt₃a₃) = L/(r) (133,1)

при любых целых п_г, /г₂, п₃ (а₁₍ а₂, а₃—основные периоды решетки).

Разложим периодическую функцию U (г) в тройной ряд Фурье. Это разложение можно написать в виде

(У = 2(Уье'^Ьг, (133,2)

ь

где суммирование происходит по всем возможным значениям вектора Ь. Эти возможные значения b определяются из требова­ния, чтобы функция U, представленная в виде ряда (133,2), удовлетворяла условию периодичности (133,1). Это значит, что все экспоненциальные множители не должны меняться при за­мене г на r + а, где а—любой из периодов решетки. Для этого необходимо, чтобы скалярное произведение ab было всегда целым кратным от 2л. Выбирая в качестве а последовательно основные периоды а₁₍ а₂, а₃, мы должны, следовательно, иметь

а₁Ь = 2яр₁, а₂Ь = 2яр₂, а₃Ь = 2яр₃,

где p_lt р₂, р₃ — целые положительные или отрицательные числа (включая нуль). Решение этих трех уравнений имеет вид

b = p₁b₁ + p₂b₂ + p₃b₃, (133,3)

где векторы Ь,- определяются через а,- посредством bi = ^[a₂a₃], b^j^a,], b₃ = ^-[a₁a₂], и = а₁[а₂а₃]. (133,4)

Таким образом, мы определили возможные значения вектора Ь. Суммирование в (133,2) распространяется по всем целым значе­ниям p_lt р₂, р₃.

Геометрически произведение t) = a₁[a₂a₃] представляет собой объем параллелепипеда, построенного на векторах а_г, а₂, а₃, т. е. объем элементарной ячейки; произведения же [а^,] и т. д. изо­бражают площади трех граней этой ячейки. Векторы Ь,- имеют, следовательно, размерность обратной длины, а по величине равны умноженным на 2я обратным высотам параллелепипеда, пост­роенного на векторах а_х, а₂, а₃.

Из (133,4) видно, что между Ь,-и а,-имеют место соотношения

(0, если i Ф1г,

2я, если i = k. ⁽¹³³'⁵⁾

Это значит, что вектор Ъ_г перпендикулярен к векторам а₂, а₃ и аналогично для b₂, Ь₃.

Определив векторы Ь,-, мы можем формально построить ре­шетку с основными периодами b_x, b₂, Ь₃. Построенная таким образом решетка носит название обратной, а векторы b_lf b₂, b₃ называются периодами (основными) обратной решетки¹).

Вычислим объем элементарной ячейки обратной решетки. Он равен

v' = bj [Ь₂Ь₃]. Подставляя сюда выражения (133,4), находим

^v' = t^a2^as] П> A] [ал]] = ([a₂a_s] а₄) ([a₃a_t] а₂),

или окончательно:

(133,6)

Очевидно, что ячейка обратной решетки триклинной решетки Бравэ тоже является произвольным параллелепипедом. Анало­гично обратные решетки простых решеток Бравэ других систем тоже являются простыми решетками той же системы; например, обратная решетка простой кубической решетки Бравэ тоже имеет простую кубическую ячейку. Легко, далее, убедиться при по­мощи простого построения в том, что обратная решетка гране-центрированных решеток Бравэ (ромбической, тетрагональной и кубической) представляет собой объемноцентрированную решетку той же системы; при этом объем параллелепипеда Бравэ обрат­ной решетки v'₀ = 8(2я)³/У/, где v_f—объем параллелепипеда Бравэ

^х) Определение (133,4), принятое в современной физической литературе, отличается множителями 2п от определения, принятого в чистой кристалло­графии.

прямой решетки. Обратно, прямой объемноцентрированной ре­шетке отвечает гранецентрированная обратная решетка, причем снова v) = (2n)³8/v_v. Наконец, для прямой решетки сцентрирован­ными основаниями обратная решетка тоже имеет ячейки с цен­трированными основаниями, причем v'_b=-(2я)³4/у_ь.

Как известно, уравнение вида br = const, где b — постоянный вектор, описывает плоскость, перпендикулярную к вектору b и находящуюся на расстоянии const/cj от начала координат. Вы­берем начало координат в каком-нибудь из узлов решетки Бравэ, и пусть Ь = р₁Ь₁ + Р2Ь₂+РзЬз есть какой-нибудь вектор обратной решетки (р_1У р_г, р₃—целые числа). Написав также г в виде а = = «^ + «2*2 + 13*31 получаем уравнение плоскости вида

Ъ&/2п = п₁р₁ + п₂р₂ + п₃р_а = т, (133,7)

где т—заданная постоянная. Для того чтобы это уравнение представляло собой плоскость, заполненную бесконечным множе­ством узлов решетки Бравэ (о таких плоскостях говорят, как о кристаллических), надо, чтобы оно удовлетворялось набором целых чисел п_1г п₂, п₃. Для этого, очевидно, постоянная т тоже должна быть целой. При заданных р_и р₂, р₃ и пробегающей раз­личные целые значения постоянной т уравнение (133,7) опреде­ляет, следовательно, бесчисленное множество кристаллических плоскостей, которые все параллельны друг другу. Каждому век­тору обратной решетки соответствует определенное указанным способом семейство параллельных кристаллических плоскостей.

Числа p_lt р₂, р₃ в (133,7) можно представлять себе всегда взаимно простыми, т. е. не имеющими общего делителя, за исклю­чением единицы. Если такой делитель имелся бы, то можно было бы разделить на него обе стороны уравнения, причем получи­лось бы уравнение того же вида. Числа р_х, р₂, р₃ называются индексами Миллера данного семейства кристаллических плоско­стей и обозначаются как (р_гр₂р₃).

Плоскость (133,7) пересекает оси координат (выбранные вдоль основных периодов а_1; а,, а₃) в точках majp,, та₂/р₂, ma₃lp_t. Отношение длин отрезков (измеренных соответственно в едини­цах а_г, а₂, а₃), отсекаемых плоскостью от осей координат, есть

Дата добавления: 2014-11-07