
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Кинетический момент системы
|
|
|
|
Рассмотрим систему материальной точки и выберем точку Мk массой mк,скорость которой Vk, на нее действуют внешние и внутренние силы 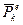 и
и  . Тогда для системы и точек:
. Тогда для системы и точек:
; 
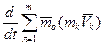 =
=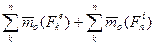 К=1…….n
К=1…….n
↓ ↓
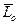 кин.мом.сист.
кин.мом.сист.  -главный момент внешних сил
-главный момент внешних сил
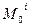 -главный момент внутренних сил равен 0
-главный момент внутренних сил равен 0
Тогда: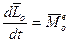 (7). Тогда формула (4) выражает теорему о изменении кинетического момента системы в дифференциальной форме: векторная производная от момента количества движения системы по времени относительно центра 0 равна главному моменту внешних сил относительно такого же центра.
(7). Тогда формула (4) выражает теорему о изменении кинетического момента системы в дифференциальной форме: векторная производная от момента количества движения системы по времени относительно центра 0 равна главному моменту внешних сил относительно такого же центра.
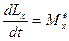 (4) в координатной форме:
(4) в координатной форме: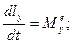

Следствие: закон сохранения кинетического момента системы: если 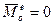 (главный момент внешних сил относительно неподвижного центра = О), то и кинетический момент системы есть величина постоянная.
(главный момент внешних сил относительно неподвижного центра = О), то и кинетический момент системы есть величина постоянная.
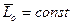 т.е.
т.е.  (5)
(5)
Кинетический момент твердого тела при вращении вокруг неподвижной оси
Вычислим  для точки массой m:
для точки массой m: 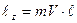
Для всего тела: 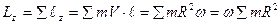
Здесь 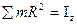 -момент инерции тела.
-момент инерции тела.
Следовательно 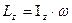
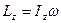 кинетический момент твердого тела относительно оси равен произведению моменту инерции тела на угловую скорость.
кинетический момент твердого тела относительно оси равен произведению моменту инерции тела на угловую скорость.
Для демонстрации закона сохранения кинетического момента системы представлена платформа Жуковского: ℓ→R
|
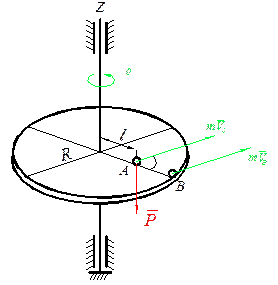
Дано: 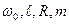
Найти: при переходе точки на край диска
I. 
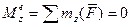
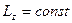 т.е.
т.е. 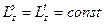
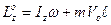 =
= 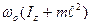
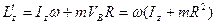
↓ ↓
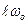
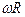
Т. к.. 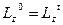 , то:
, то: 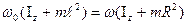 ,
, 
II. Если 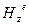 не равен 0:
не равен 0:
Если 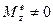 пусть
пусть 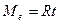
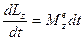 интегрируя:
интегрируя:
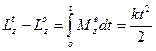
Здесь:
2) 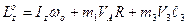 (2) В момент t сек точка массой
(2) В момент t сек точка массой  переходит в положение В, имея при этом относительную скорость
переходит в положение В, имея при этом относительную скорость 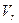 , тогда
, тогда
↓ ↓
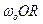
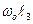
3) 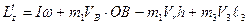 (3), где
(3), где 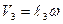 т. к.
т. к. 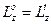 получаем
получаем 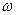 , приравнивая равенства (2) и (3)
, приравнивая равенства (2) и (3)
|

|
|
|
|
|
Дата добавления: 2014-10-15; Просмотров: 635; Нарушение авторских прав?; Мы поможем в написании вашей работы!