Гипербола

Эллипс

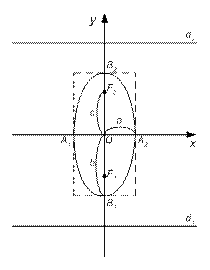
Эллипсом называется множество точек плоскости, сумма расстояний от каждой из которых до двух данных точек плоскости F ₁ и F ₂, называемых фокусами, есть величина постоянная, равная 2а, большая, чем расстояние между фокусами 2с.

Пусть точка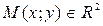

Эллипс =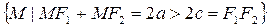

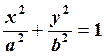- каноническое уравнение (51)

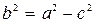
Эллипс пересекает ось Ox в точках А ₁ (-а; 0), А ₂ (а; 0), а ось Oy – в точках В ₁ (0; -b), В ₂ (0;-b). Точки А ₁, А ₂, В₁, В ₂ – вершины эллипса.

А ₁ А ₂ =2а – большая ось, а – большая полуось

В ₁ В ₂= 2b – малая ось, b – малая полуось

F ₁ (-с;0), F ₂ (с;0) – фокусы эллипса.

F ₁ F ₂ - фокальное расстояние

Эксцентриситет эллипса – число, равное отношению фокального расстояния к длине большой оси

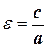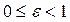, (52)

Эксцентриситет характеризует форму эллипса. Чем больше эксцентриситет, тем больше эллипс вытянут вдоль большой оси. Если e =0 Þ с=0 и а=b. В этом случае эллипс вырождается в окружность с центром в начале координат: 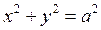или .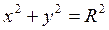

Отрезки , 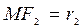- фокальные радиусы. Для любой точки М(x,y), принадлежащей эллипсу, верно: , .

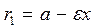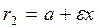Прямые 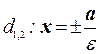- директрисы эллипса (53)

Директрисы перпендикулярны фокальной оси и не пересекают эллипс.

Свойства эллипса

1° (51)эллипс расположен внутри прямоугольника со сторонами 2а и 2b.

2° Эллипс симметричен относительно начала координат и осей Ox, Oy.

3° Директориальное свойство эллипса:

Для любой точки М, принадлежащей эллипсу, справедливо отношение: 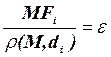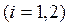, где e - эксцентриситет эллипса (54)

Если a>b, то большая ось эллипса равна 2а, фокусы F ₁, F ₂Î Ox и .

Если a < b, то большая ось 2b и фокусы лежат на оси Oy, т.е.

,

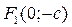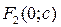
- уравнения директрис эллипса.

Если центр эллипса находится в точке М ₀(x ₀ ;y ₀), а оси параллельны координатным осям, то его уравнение имеет вид: .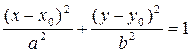

Гиперболой называется множество точек плоскости, для каждой из которых абсолютное значение разности расстояний до двух данных точек плоскости F_1, F₂, называемых фокусами, есть величина постоянная, равная 2а, меньшая, чем расстояние между фокусами 2с.

Если точка 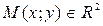, то

Гипербола = .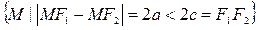

- каноническое уравнение (55)

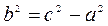
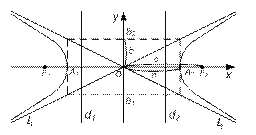
Гипербола пересекает ось Ox в точках А ₁ (-а;0), А ₂ (а;0) – вершинах гиперболы и не пересекает ось Oy.

А ₁ А ₂ =2а – действительная ось, а – действительная полуось;

В ₁ В ₂= 2b – мнимая ось, b – мнимая полуось;

Прямоугольник со сторонами 2а и 2b – основной прямоугольник гиперболы.

В ₁ (0;-b), В ₂ (0;-b) – точки пересечения основного прямоугольника с Oy.

Эксцентриситет гиперболы 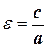, где e > 1 (56)

Чем больше e, тем больше гипербола вытянута вдоль оси Ox.

Если основной прямоугольник – квадрат, т.е. a=b (действительная и мнимая оси гиперболы равны), то гипербола равносторонняя и задана уравнением .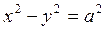

Отрезки , 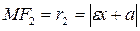- фокальные радиусы точки М, принадлежащей гиперболе.

Прямые - директрисы гиперболы (57)

Директрисы расположены внутри основного прямоугольника.

Прямые – асимптоты гиперболы (58)

Свойства гиперболы

1° (56)в полосе – a < x < a точек гиперболы нет.

2° Гипербола симметрична относительно начала координат и осей Ox, Oy. Точка О – центр гиперболы.

3° Директориальное свойство гиперболы:

Для любой точки М, принадлежащей гиперболе, справедливо отношение: 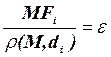, 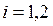(59)

Уравнение (55) определяет гиперболу, у которой действительная ось совпадает с осью Ox и .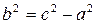

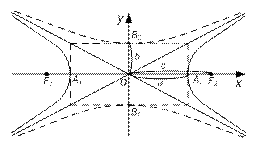
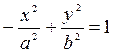Уравнение определяет гиперболу с действительной осью Oy, где

,

.

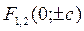
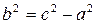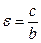
Гиперболы, заданные уравнениям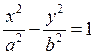и

и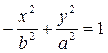

имеют общие асимптоты и называются сопряженными гиперболами.

Если центр гиперболы находится в точке М ₀(x ₀ ;y ₀), а оси параллельны координатным осям, то ее уравнение имеет вид: .

Дата добавления: 2014-10-22