Угол между прямой и плоскостью. Взаимное расположение прямой и плоскости

Взаимное расположение прямой и плоскости

Угол между прямыми в пространстве

За угол между двумя прямыми в пространстве принимают угол j между направляющими векторами прямых.

Для нахождения острого угла между прямыми используют формулу:

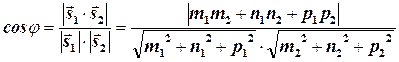(47)

.

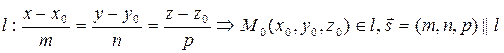
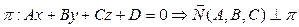Возможные случаи взаимного расположения прямой и плоскости можно описать следующим образом:

1)

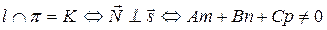
2)

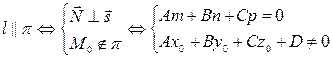
3)

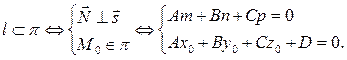
За угол j между прямой и плоскостью принимают угол между прямой и ее проекцией на эту плоскость.

Пусть 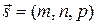- направляющий вектор прямой l

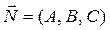- нормальный вектор плоскости p.

Обозначим 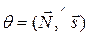, , 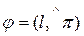тогда

.

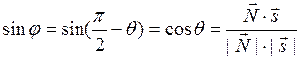Считая 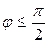, получаем

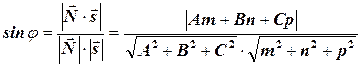(48)

Условия параллельности и перпендикулярности прямой и плоскости

.

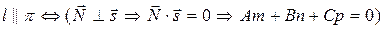
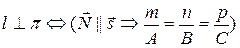Пример 2.18. Составить канонические, параметрические и общие уравнения прямой, проходящей через точку М₀(-1;0;2) параллельно оси O z.

Решение: По условию задачи l ||O z Þнаправляющим вектором прямой может служить орт оси O z - вектор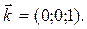

Запишем канонические уравнения прямой

(43) Þ l: .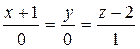

Приравнивая попарно отношения, получим общие уравнения прямой

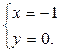
Параметрические уравнения прямой имеют вид:

.

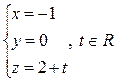Ответ: 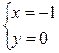- общие уравнения прямой.

Пример 2.19. Даны координаты вершин треугольника А (2;3;-1), В (1;-2;0), С (-3;2;2). Составить уравнение медианы АМ и найти ее длину.

Решение: Найдем координаты точки М – середины отрезка ВС:

.

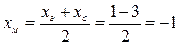
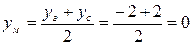
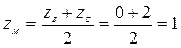Следовательно, 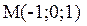. Тогда 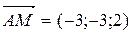- направляющий вектор медианы.

Составим канонические уравнения прямой АМ:

(43) Þ .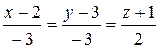

Найдем длину отрезка АМ:

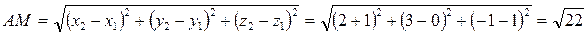
Ответ: , .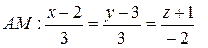

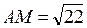Пример 2.20. Привести общие уравнения прямой к каноническому виду

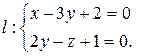
Решение: Прямая задана как линия пересечения двух плоскостей с нормальными векторами 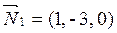, 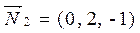. Тогда направляющий вектор прямой имеет вид:

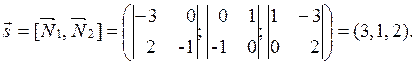
Возьмем какую-нибудь точку 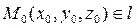, для чего одной из координат в общем уравнении придадим произвольное значение. Пусть х ₀=1, тогда

.

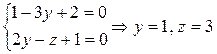Таким образом: 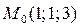и канонические уравнения прямой имеют вид

.

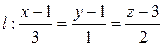Ответ: .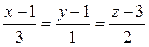

Пример 2.21. Доказать, что данные прямые перпендикулярны

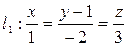
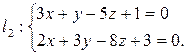
Решение: Найдем направляющие векторы данных прямых

.

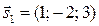
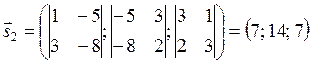Вычислим скалярное произведение векторов

.

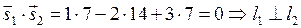Ответ: .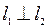

Пример 2.22. Установить взаимное расположение прямой l и плоскости a. В случае пересечения прямой и плоскости найти точку пересечения и угол между ними

а)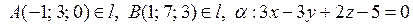

б)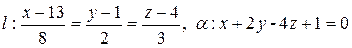

в) .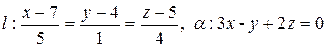

Решение:

а) В качестве направляющего вектора прямой l можно взять вектор 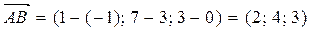, в качестве вектора нормали плоскости a - вектор .

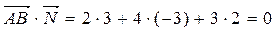Þ l || a или l Ì a.

Проверим, лежит ли, например, точка А, принадлежащая прямой l, в плоскости a:

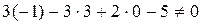Þ A Ï a Þ l || a.

б) М ₀(13;1;4)Î l, 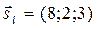- направляющий вектор прямой l,

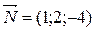- нормаль плоскости a.

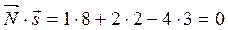Þ l || a или l Ì a.

Проверим, лежит ли точка М ₀ в плоскости a

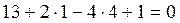Þ М ₀ Î a Þ l Ì a.

в) , .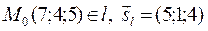

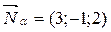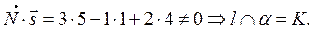
Найдем координаты точки К из системы

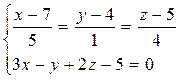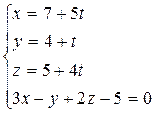Þ Þ

Þ 3(7 + 5 t) - (4 + t) + 2(5 + 4 t) – 5 = 0 Þ 22 t + 22 = 0 Þ

Þ t = -1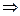 x = 7 – 5 = 2, y = 4 – 1 = 3, z = 5 – 4 = 1 Þ К (2; 3; 1).

Угол между прямой и плоскостью вычислим по формуле (48)

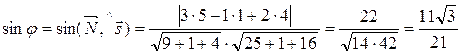Þ

.

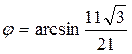Ответ: а) l || a

б) l Ì a.

в) .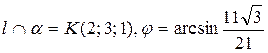

Пример 2.23. Составить уравнение плоскости, проходящей через точку 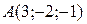и перпендикулярно к прямой .

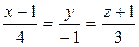Решение: Направляющий вектор прямой можно принять за вектор нормали искомой плоскости: .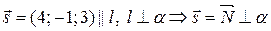

Запишем уравнение плоскости, проходящей через точку 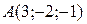перпендикулярно вектору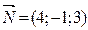

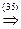
4(x - 3) - (y + 2) + 3(z + 1) = 0 или 4 x - y + 3 z - 11=0.

Ответ: 4 x - y + 3 z - 11 = 0

Пример 2.24. Составить уравнения перпендикуляра опущенного из точки А(1; 2; 3) на плоскость .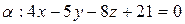

Решение: Вектор 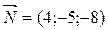- нормаль плоскости, может служить направляющим вектором искомой прямой l.

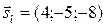, А(1; 2; 3)Î l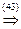

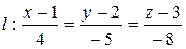- канонические уравнения перпендикуляра.

Ответ: .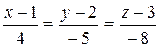

Дата добавления: 2014-10-22