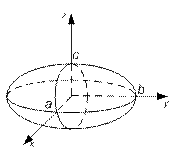
Эллипсоиды

Поверхности второго порядка

Поверхностью второго порядка называется множество точек пространств, координаты x, y и z которых удовлетворяют уравнению второй степени:

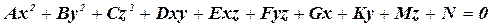(62)

Коэффициенты A, B, C, D, E, F ≠ 0 одновременно.

Уравнение (62) есть общее уравнение поверхности второго порядка

Одним из основных методов определения геометрического вида поверхности второго порядка является метод сечений. Суть метода состоит в том, что вывод о форме поверхности основывается на исследовании формы сечений этой поверхности некоторыми плоскостями (обычно используют координатные плоскости x= 0, y= 0, z= 0 или параллельные им плоскости: x=h, y=h, z=h).

Рассмотрим основные типы поверхностей второго порядка, указав их канонические уравнения.

Эллипсоидом называется поверхность, определяемая в ПДСК уравнением:

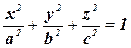(63)

Уравнение (63) называется каноническим уравнением эллипсоида, где числа a, b, c - полуоси эллипсоида

Переменные x, y, z входят в уравнение (63) в четной степени Þ эллипсоид симметричен относительно всех координатных плоскостей и начала координат.

Эллипсоид – замкнутая, ограниченная поверхность, т.к. .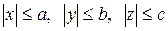

Точки пересечения эллипсоида с осями координат

A₁(a; 0; 0), A₂(- a; 0; 0), B₁(0; b; 0), B₂(0; - b; 0), C₁(0; 0; c), C₂(0; 0; - c) называются вершинами эллипсоида.

Рассмотрим сечение эллипсоида плоскостью z=h, параллельной О ху, где h ÎR. Линия сечения определяется системой:

.

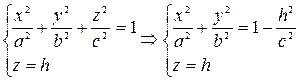Исследуем полученную систему:

1. | h | =c Þ 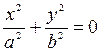Þ плоскости z=h касаются эллипсоида в точках C_1,2(0; 0; 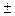c), которые называют вершинами эллипсоида.

2. | h | >c Þ 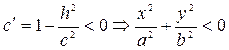Þ плоскости z=h не имеют точек пересечения с эллипсоидом.

3. | h | <c Þ 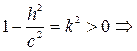линией пересечения является эллипс:

Например, при h= 0 в сечении эллипсоида плоскостью z= 0, получаем эллипс, определяемый системой:

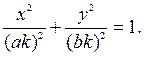
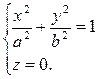
Аналогичная ситуация складывается при рассмотрении сечений эллипсоида плоскостями x=h, y=h.

Если полуоси эллипсоида различны – эллипсоид трёхосный, если две равны - эллипсоид вращения. При a=b=c=r имеем сферу:

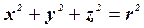(63¢)

Дата добавления: 2014-10-22