КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Парабола
|
|
|
|
Параболой называется множество точек плоскости, равноудаленных от данной точки F (фокуса) и данной прямой d (директрисы).
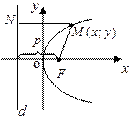 Парабола =
Парабола = 
Число p - расстояние от фокуса параболы F до директрисы d, т.е. 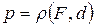 , р >0 – фокальный параметр параболы.
, р >0 – фокальный параметр параболы.
y 2 =2px – каноническое уравнение (60)
Директриса параболы  (61)
(61)
Фокус параболы  .
.
Свойства параболы:
1° Ось Ox - ось симметрии параболы.
2° Для любой точки М, принадлежащей параболе:
 - фокальный радиус точки.
- фокальный радиус точки.
3° Для любой точки М, принадлежащей параболе, справедливо отношение:  , поэтому эксцентриситет параболы принимают за единицу.
, поэтому эксцентриситет параболы принимают за единицу.
Основные случаи расположения параболы:
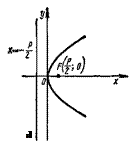 | 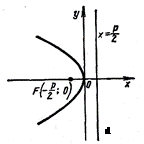 | ||
 ,
, 
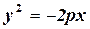 ,
, 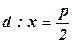


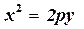 ,
, 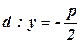
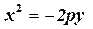 ,
, 
Если вершина параболы расположена в точке М 0(x 0 ;y 0), то ее уравнение имеет вид 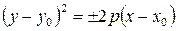 или
или 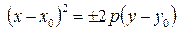 .
.
Эллипс, гипербола и парабола являются примерами кривых второго порядка на плоскости. Кроме названных кривых, существуют и другие виды кривых второго порядка, перечень которых приведен в таблице.
| № | Тип кривой | Каноническое уравнение кривой | Примечание |
| 1. | Эллипс | 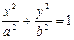
| |
| 2. | Мнимый эллипс | 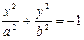
| действительных точек нет |
| 3. | Гипербола | 
| |
| 4. | Пара пересекающихся прямых | 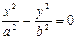
| уравнения
прямых: 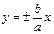
|
| 5. | Пара мнимых пересекающихся прямых | 
| действительная точка (0;0) |
| 6. | Парабола | у 2 =2 рх | |
| 7. | Пара параллельных прямых | у 2 - а 2 =0 | уравнения прямых: у =± а |
| 8. | Пара мнимых параллельных прямых | у 2 + а 2 =0 | действительных точек нет |
| 9. | Пара совпадающих прямых | у 2 =0 | уравнения прямых: у =0 |
Пример 3.1. Привести уравнение кривой к каноническому виду. Построить кривую.
а) 
б)  .
.
Решение:
а) Выделим полные квадраты по x и по y
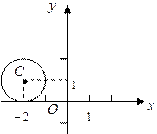
 Þ
Þ
 - окружность с центром в точке С(-2;1) и радиусом R=1
- окружность с центром в точке С(-2;1) и радиусом R=1
б)  Þ
Þ
 - окружность, где
- окружность, где 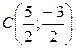 ,
,  .
.
Ответ: а) 
б) 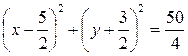 .
.
Пример 3.2. Составить уравнение окружности, касающейся осей координат и проходящей через точку М (2;4).
Решение:  .
.
Т.к. окружность касается осей координат, то  Þ уравнение окружности:
Þ уравнение окружности:  .
.
Точка М (2;4) принадлежит окружности Þ
принадлежит окружности Þ  Þ
Þ

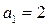 ,
, 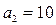
Ответ:  или
или  .
.
Пример 3.3. Составить уравнение окружности, диаметром которой является отрезок прямой  , заключенный между осями координат.
, заключенный между осями координат.
 Решение: Приведем уравнение прямой к виду «в отрезках»:
Решение: Приведем уравнение прямой к виду «в отрезках»:


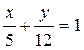 Þ в точках А (5;0) и В (0;12) прямая пересекает О х и О у.
Þ в точках А (5;0) и В (0;12) прямая пересекает О х и О у.
По условию, АВ – диаметр окружности, следовательно, С - середина АВ.
 Þ С(
Þ С( ;6).
;6).
 .
.
Ответ: 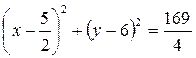 .
.
Пример 3.4. Написать уравнение диаметра окружности, заданной уравнением  , который перпендикулярен прямой
, который перпендикулярен прямой  .
.
Решение: Диаметр d проходит через центр окружности. Найдем координаты центра окружности, для чего приведем уравнение окружности к каноническому виду:

 Þ С(3;-7)- центр окружности.
Þ С(3;-7)- центр окружности.
По условию  Þ
Þ 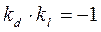 Þ
Þ  т.к.
т.к. 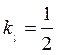 .
.
Воспользуемся уравнением прямой, проходящей через данную точку с данным угловым коэффициентом: 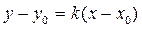 Þ
Þ  Þ
Þ
 Þ
Þ 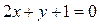 .
.
Ответ: 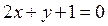 .
.
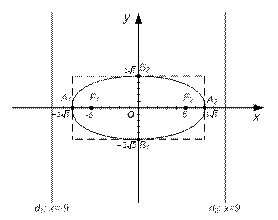
Пример 3.5. Найти полуоси, координаты вершин, фокусов, эксцентриситет, уравнения директрис эллипса, заданного уравнением 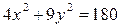 . Сделать чертеж.
. Сделать чертеж.
Решение: Приведем уравнение эллипса к каноническому виду:

 Þ
Þ  ,
, 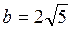
|
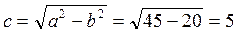
 -вершины эллипса
-вершины эллипса
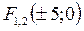 - фокусы эллипса
- фокусы эллипса
 .
.
Уравнения директрис 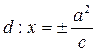 или
или 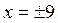 .
.
Ответ: 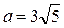 ,
,  ,
, 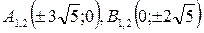 ,
, 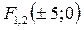
 ,
, 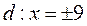 .
.
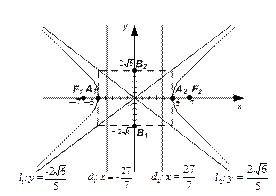
Пример 3.6. Найти полуоси, координаты вершин, фокусов, эксцентриситет, уравнения директрис и асимптот гиперболы, заданной уравнением  . Сделать чертеж.
. Сделать чертеж.
Решение: Приведем уравнение гиперболы к каноническому виду:
|

 - каноническое уравнение Þ
- каноническое уравнение Þ
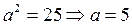



 - вершины гиперболы
- вершины гиперболы
 - фокусы гиперболы
- фокусы гиперболы
Уравнения директрис:  или
или 
Уравнения асимптот:  или
или 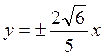 .
.
Ответ: 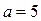 ,
,  ,
,  ,
, 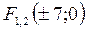
 ,
,  ,
, 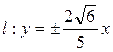 .
.
Пример 3.7. Привести уравнение кривой к каноническому виду:  . Построить кривую и найти эксцентриситет.
. Построить кривую и найти эксцентриситет.
Решение: Выделим полные квадраты по х и по у:

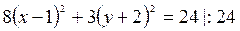
 Þ центр эллипса находится в точке С(1;-2)
Þ центр эллипса находится в точке С(1;-2)

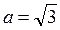 ,
, 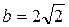

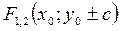 Þ
Þ 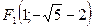 ,
, 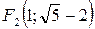
 Þ
Þ 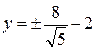
Ответ:  - эллипс,
- эллипс, 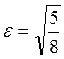 .
.
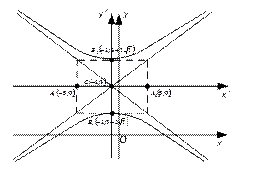
Пример 3.8. Привести уравнение кривой к каноническому виду и построить кривую
а) 
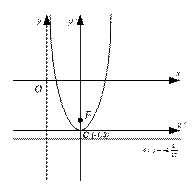
б)  .
.
Решение:
а) Выделим полные квадраты по х и у:
|
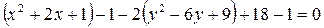
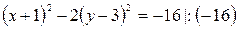
 - гипербола
- гипербола
С(-1;3) - центр гиперболы
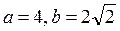 - полуоси гиперболы
- полуоси гиперболы
 Þ
Þ  .
.
|
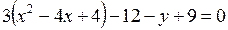

 - парабола
- парабола
С(2;-3) - вершина параболы
Найдем параметр параболы: т.к.  , то
, то  . Тогда
. Тогда  .
.
Ответ: а) 
б)  .
.
|
|
|
|
|
Дата добавления: 2014-10-22; Просмотров: 2061; Нарушение авторских прав?; Мы поможем в написании вашей работы!