Дифференциальные уравнения 1-го порядка

Дифференциальные уравнения 1-го порядка имеют вид: 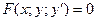(1)

Если уравнение (1) решить относительно 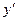, то оно называется уравнением разрешённым относительно производной и имеет вид: 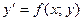(2)

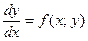
Одной из важных задач теории дифференциальных уравнений является задача Каши:

Среди всех решений дифференциального уравнения найти то, которое при 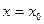принимает значение 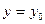, т.е. найти такую функцию 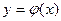, которая удовлетворяла бы дифференциальному уравнению и условию:

Значения называются начальными значениями Каши.

Они записываются 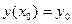или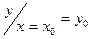

Геометрически задача Каши формулируется так:

Среди всех интегральных кривых дифференциального уравнения (2) найти ту которая проходит через заданную точку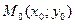

y

M₀

x

⁰

Решение задачи Каши может быть и не единственным, может и вообще не существовать.

Справедлива следующая теорема (о существовании и единственности решений дифференциального уравнения)

Т. Если уравнение 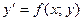, функция 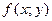непрерывна со своей частной производной 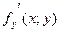в некоторой области 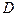и точке , то существует единственное решение этого уравнения (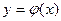- решение), удовлетворяющее начальному условию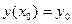

Геометрически это означает, что через единственную точку можно провести единственную интегральную кривую, т.е. интегральные кривые не пересекаются между собой.

y

M₀

D

0 x

Введём понятие общего и частного решения дифференциальных уравнений.

О. Общим решением дифференциального уравнения (1) или (2) в области D называется функция 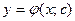, зависящая от х и произвольной постоянной с и удовлетворяющая условиям:

1)Она удовлетворяет дифференциальному уравнению при любом значении с.

2)Какова бы ни была внутренняя точка , существует единственное значение постоянной 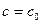такое, что функция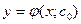

удовлетворяет начальному условию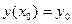

О. Частным решением дифференциального уравнения называется такое решение, которое получается из общего решения при некотором частном значении произвольной постоянной.

Часто решение дифференциального уравнения получается в форме, неразрешённой относительно переменной y.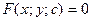

Соотношение вида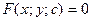, неявно определяющее решение, называется общим интегралом дифференциального уравнения 1-го порядка.

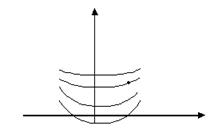
Геометрически общий интеграл и общее решение представляют собой семейство интегральных кривых зависящих от общей произвольной постоянной.

О. Решение, в каждой точке которого нарушено свойство единственности называется особым.

Дата добавления: 2014-10-22