Основные понятия. Дифференциальные уравнения высших порядков

Дифференциальные уравнения высших порядков.

Ый тип. Уравнение Бернулли.

(1)

где P(x) и Q(x) – определённые непрерывные функции на [a;b]

, , .

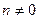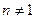Уравнение Бернулли приводится к линейному уравнению путём подстановки:

Разделим (1) на :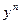

обозначим:

- линейное уравнение, оно решается

подстановкой

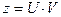
При решении уравнений Бернулли их не надо приводить к линейным, а сразу решать как линейное уравнение подстановкой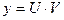

Те понятия, которые были сформулированы для дифференциальных уравнений первого порядка без изменений переносятся на дифференциальные уравнения высших порядков.

Рассмотрим дифференциальное уравнение 2-го порядка.

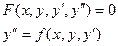(1)

(2)

Как и для дифференциального уравнения 1-го порядка, решения дифференциального уравнения 2-го порядка определяются неоднозначно, поэтому возникла необходимость введения дополнительных условий, которые позволили бы выделить из множества решений некоторое решение, обладающее определёнными свойствами.

Задача Каши.

Среди всех решений дифференциального уравнения (2) найти такое, которое удовлетворяет заданным условиям:

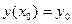
(3)

где - заданные числа или начальные данные Каши.

Замечание: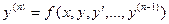

его начальные условия:

Теорема Каши: (теорема существования и единственности решения)

Если функция 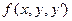непрерывна в пространстве области D вместе с частными производными , то существует решение уравнения (2), удовлетворяющее начальным условиям (3)

О. Функция 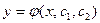, зависящая от с₁ и с₂ называется общим решением дифференциального уравнения , если выполняются два условия:

1) функция 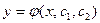удовлетворяет дифференциальное уравнение при любых значениях произвольных постоянных с₁ и с₂

2) какими бы ни были заданы начальные условия (лишь бы они принадлежали области D и удовлетворяли условиям теоремы Каши), можно подобрать произвольные постоянные (с₁, с₂) так, чтобы решение 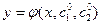удовлетворяло начальным условиям.

О. Частным решение дифференциального уравнения является решение получаемое из общего решения при фиксированных значениях произвольных постоянных.

Дата добавления: 2014-10-22