Линейные однородные уравнения с постоянными коэффициентами

(1)

а₁ и а₂ = const

Мы доказали, что если у₁ и у₂ - линейные независимые решения (образуют фундаментальную систему решений), то с их помощью легко построить общее решение уравнения (1)

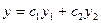
Будем искать решение в виде:

(2).

где k – неизвестная const.

(2) – решение (1)

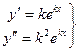подставим в уравнение (1)

т.к.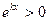

(3) – характеристическое уравнение

решив (3) находим k₁ и k₂

Исследуем характеристическое уравнение:

1-ый случай: D >0

k₁ ≠ k₂ - действительные различные корни

2-ой случай: D ≠0

k₁ = k₂ - действительные равные корни

3-ий случай: D<0

k_1,2 = - комплексные корни

Рассмотрим:

I случай: k₁ ≠ k₂ - действительные различные корни

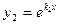; - решение дифференциального уравнения (1) частные

=> у₁ и у₂ - линейно независимые функции

Например: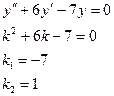

Ответ: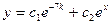

II случай: k₁ = k₂ действительные равные корни.

В этом случае можно записать одно из решений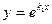

Второе решение у₂ (линейно независимое от у₁ ) ищем в виде:

где U(x) – независимая функция, которую надо определить.

т.к. нужно одно значение функции, полагаем с₂ =0, с₁ =1, тогда U(x) = x

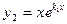
Ответ:

Например: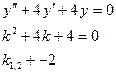

Ответ:

III случай:

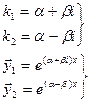
комплексные корни

комплексное решение дифференциального

уравнения (1) (они линейно независимы).

Наша задача – получить два линейно независимых действительных решения. Для этого первое комплексное решение запишем в виде:

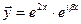
Воспользуемся формулой Эйлера:

(на основании теоремы (Т.4.) известно, что если комплексная функция является решением линейного однородного уравнения, то и U(x), и V(x) тоже есть решения этого уравнения)

Действительная часть:

Мнимая часть:

На основании этого свойства заключаем, что для случая комплексных корней характеристического уравнения имеют два линейно независимых действительных решения.

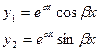
Докажем, что они линейно независимые:

частное решение

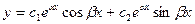
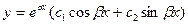
Методы нахождения частных решений линейных неоднородных уравнений:

(1)

На основании структуры общего решения линейного неоднородного уравнения, следует:

I. метод подбора частных решений по виду правой части.

(метод неопределённых коэффициентов)

в дифференциальном уравнении (1) - известная функция

не приводя выводов укажем формулу, в которой следует искать частное решение в зависимости от вида правой части (имеет специальный вид)

Т.1. Если правая часть линейного неоднородного дифференциального уравнения (1) с постоянным коэффициентами имеет вид: 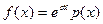, где p(x) – многочлен n -ой степени и α – коэффициент в показателе e, не являющийся корнем характеристического уравнения, то существует частное решение вида:

где М(х) – некоторый многочлен n -ой степени:

если же α является корнем характеристического уравнения кратности «r», тогда частное решение имеет вид:

Т.2. Если правая часть линейного неоднородного дифференциального уравнения (1) имеет вид:

где P(x) и Q(x) – многочлены (могут быть разных степеней, n – наибольшая из их степеней)

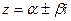- не является корнем характеристического уравнения, то существует частное решение вида:

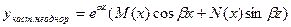
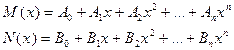где

если же 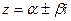- является корнем характеристического уравнения кратности «r», то частное решение имеет вид: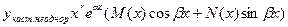

Например: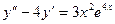

1)

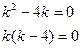
или

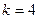
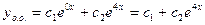
2)

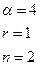
При решении конкретных примеров нужно установить вид (форму) частного решения, записав его с неопределёнными коэффициентами (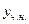). Найти 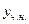, и подставим в дифференциальное уравнение (1)

Получим тождественное равенство 2-ух многочленов n -ой степени (частный случай: n =2).

Сравнивая коэффициенты при одинаковых неизвестных слева и справа, получим систему уравнений для нахождения неопределённых коэффициентов.

Например: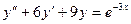

1)

2)

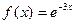
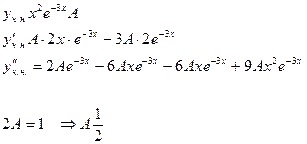
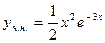
Ответ:

II. Метод вариации произвольных постоянных.

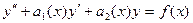(1)

Но на основании структуры общего решения линейного дифференциального уравнения следует, что для составления общего решения

Рассмотрим метод, который позволяет найти частное решение неоднородного уравнения (), при условии, что известно общее решение, соответствующее неоднородному уравнению ().

Этот метод применим к любой правой части.

Будем искать общее решение неоднородного дифференциального уравнения (1) в той же форме (2), только вместо произвольных постоянных возьмём функции, зависящие от х (варьируем постоянные)

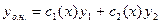(3)

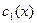где и 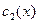- пока неизвестные функции.

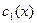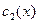Выберем и так, чтобы функция (3) удовлетворяла дифференциальное уравнение (1).

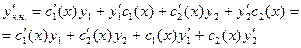(4)

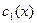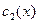Подберём и так, чтобы выполнялось условие:

(5)

Тогда уравнение (4) примет вид:

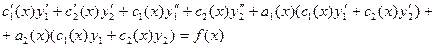
у₁ и у₂ - решение однородного уравнения, поэтому равно 0

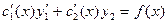(6)

=> для нахождения 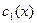и 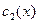получаем систему уравнений:

, т.к. у₁ и у₂ линейно независимые.

=> система имеет единственное решение

подставим в уравнение (3)

Ответ:

Например:

1)

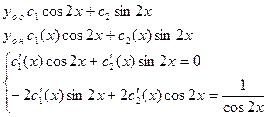
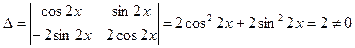=> система имеет единственное решение

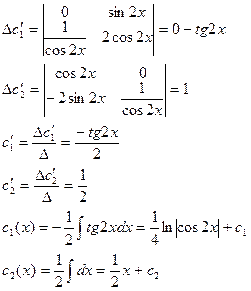
Ответ:

Дата добавления: 2014-10-22