Геометрическая прогрессия

Числовые ряды. Понятие о ряде. Сумма рядов.

Ряды.

Система дифференциального уравнения 1-го порядка в нормальной форме.

(линейные системы с постоянными коэффициентами)

Во многих задачах математики, физики и техники определить сразу несколько функций, связанных между собой несколькими дифференциальными уравнениями. Совокупность таких уравнений называется системой дифференциального уравнения.

Ограничимся изучением только системы уравнений 1-го порядка относительно искомых функций у₁ и у₂ и т.д. и называется она системой в нормальной форме или нормальной системой.

Например: нормальная система 3-х уравнений с 3-мя неизвестными x,y,z:

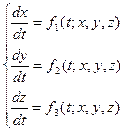(1)

О. Решением системы (1) называется совокупность функций x, y, z, удовлетворяющее каждому из уравнений этой системы

Для интегрирования системы (1) можно применить метод, с помощью которого данная система, содержащая 3 уравнения, относительно 3-х искомых функций сводится к одному уравнению 3-го порядка относительно одной неизвестной.

Этот метод называется исключением неизвестных.

(рассмотреть метод самостоятельно).

Пусть дана бесконечная последовательность чисел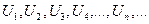

Например: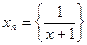

О. Выражение вида 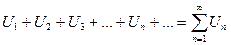(1) называется числовым рядом

Числа 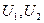и т.д. – члены ряда

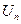- общий член ряда

Составим суммы:

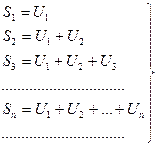(2) – частичные суммы ряда (1)

Суммы (2) называются частичными суммами ряда (1).

О. Если существует конечный предел (3) 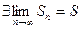, то ряд (1) называется сходящимся рядом и число S – сумма этого ряда

Если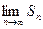не существует или равно ∞, то ряд (1) расходится или расходящийся => суммы ряда нет.

Например: (теоретически)

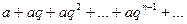(1)

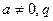- знаменатель прогресси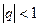и или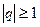

Составим n -ую частичную сумму

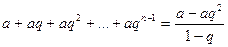
1) 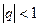, тогда

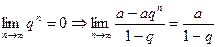
Ряд (1) сходится и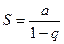

2) 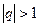, тогда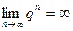

Ряд (1) расходится 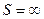(сумма не существует)

3)

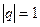
а)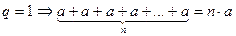

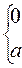
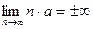т.к. ()

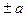б) 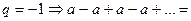(если чётное количество )

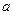(если n – нечётное)

т.к 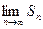принимает разное значение при n -чётном и n -нечётном

=> этот предел не существует =>ряд расходится.

Ряд (1) сходится, когда

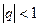
Ряд (1) расходится, когда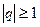

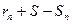- остаток ряда

Учитывая, что 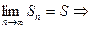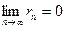- применяется при приближенных вычислениях.

Дата добавления: 2014-10-22