
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Определители квадратных матриц
|
|
|
|
Задачи для самостоятельной работы
Задача 1.1. Найти  , если А =
, если А =  , В =
, В =  .
.
Ответ: 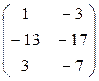 .
.
Задача 1.2. Найти произведение матриц:
1)  2)
2) 
3)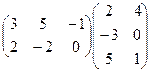 4)
4)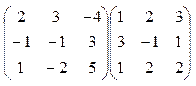
5)  6)
6)  .
.
Ответ: 1) 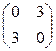 2)
2)  3)
3) 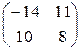 4)
4) 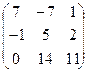 5) 7 6) (5 -19 5).
5) 7 6) (5 -19 5).
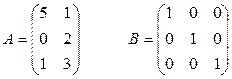
Задача 1.3. Найти те из произведений АВ и ВА, которые существуют:
1) 
2) 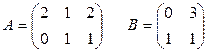
3) 
4) 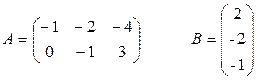
5)  .
.
 Ответ: 1)
Ответ: 1) 
2) 
3) 
4) 
5)  .
.
Задача 1.4. Найти А2 +В2, если А = , В =
, В = 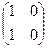 .
.
Ответ: .
.
Задача 1.5. Привести к ступенчатому виду матрицу А с помощью элементарных преобразований над строками
1) 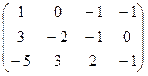 2)
2)  3)
3) 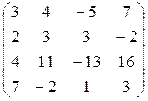 .
.
Ответ: 1)  2)
2)  3)
3)  .
.
Задача 1.6. Выяснить, является ли матрица 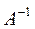 обратной к А
обратной к А
1) 
2) 
3) 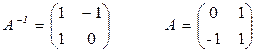 .
.
Ответ: 1) да 2) нет 3) да.
Задача 1.7. С помощью элементарных преобразований над строками найти обратную матрицу для следующих матриц
1)  2)
2)  3)
3) 
4) 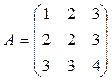 5)
5)  6)
6) 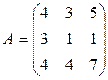 .
.
Ответ: 1)  2)
2) 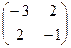 3)
3) 
4) 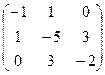 5)
5) 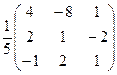 6)
6) 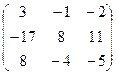 .
.
Задача 1.8. Решить матричные уравнения
1)  , если
, если 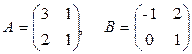
2) 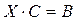 , если С =
, если С =  , В =
, В =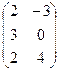
3) 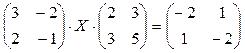
4) 
5) 
6) 
7) 
8) 
9) 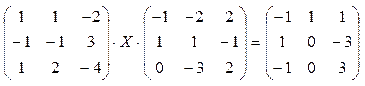
10)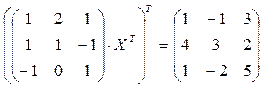
Ответ: 1) 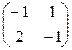 2)
2) 
3)  4)
4) 
5)  6)
6) 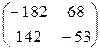
7)  8)
8) 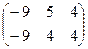
9) 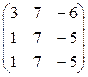 10)
10)  .
.
Задача 1.9. Является ли множество матриц 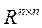 абелевой группой по сложению?
абелевой группой по сложению?
Задача 1.10. Является ли множество матриц  группой по умножению?
группой по умножению?
Задача 1.11. Доказать, что алгебра (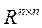 , +,
, +, 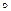 ) является некоммутативным кольцом с единицей.
) является некоммутативным кольцом с единицей.
|
|
|
|
|
Дата добавления: 2014-10-22; Просмотров: 341; Нарушение авторских прав?; Мы поможем в написании вашей работы!