Виды матриц

Понятие матрицы. Виды матриц

МАТРИЦЫ И ОПЕРАЦИИ НАД НИМИ

Матрицей размера 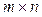над полем F называется прямоугольная таблица элементов поля F, имеющая m строк и n столбцов

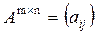или , где .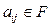

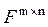- множество всех матриц размера 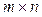над полем F.

Нулевая матрица - матрица, у которой все элементы равны нулю.

Квадратная матрица - матрица размера .

Например, - квадратные матрицы 1-го, 2-го и 3-го порядков соответственно.

Диагональная матрица 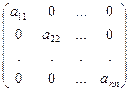- квадратная матрица, у которой элементы, не принадлежащие главной диагонали, равны нулю.

Например, - диагональная матрица 2-го порядка

- диагональная матрица 3-го порядка.

Единичная матрица 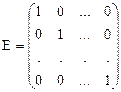- квадратная матрица, у которой элементы главной диагонали равны единице, остальные равны нулю.

Например, 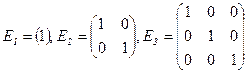- единичные матрицы

1-го, 2-го и 3-го порядков соответственно.

Верхняя (нижняя) треугольная матрица - квадратная матрица, у которой все элементы, стоящие под (над) главной диагональю, равны нулю.

Матрица-строка А = (а₁₁, а₁₂, …, а_1n) – матрица размера .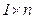

Матрица-столбец А = - матрица размера .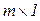

Ведущим элементом строки матрицы А называется первый (считая слева направо) ненулевой элемент строки. Столбец матрицы называется основным, если он содержит ведущий элемент какой-либо строки матрицы.

Матрица А - ступенчатая, если она удовлетворяет условиям:

1) нулевые строки матрицы (если они имеются) расположены ниже всех ненулевых строк;

2) если , ,…, 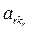- ведущие элементы ненулевых строк матрицы, то k₁ < k₂ < … < k_r.

Примеры ступенчатых матриц: нулевая матрица; матрица-строка; единичная матрица; верхняя треугольная матрица.

Две матрицы одной размерности называют равными, если равны элементы, стоящие на одинаковых местах: и а_ij = b_ij.

1.2. Операции над матрицами. Свойства операций над матрицами. Кольцо квадратных матриц

Умножение матрицы на число. При умножении матрицы на число каждый элемент матрицы умножается на это число: 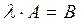, где .

Пример 1.1. Если А = 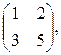то 3× А = 3×.

В частности, 0× А = О, 1× А = А.

Общий множитель всех элементов матрицы можно выносить за знак матрицы.

Пример 1.2. .

Сложение матриц. Сложение двух матриц одинаковой размерности производится поэлементно: А + В = С, где с_ij = а_ij + b_ij (i = 1,…, m; j = 1,…, n).

Дата добавления: 2014-10-22