Линейное, евклидово и нормированное пространства

Определение. Множество М элементов x,y,z…любой природы называют линейным (аффинным, векторным) пространством, если выполнены требования:

1-е. Имеется правило, по которому любым двум элементам х и у из М ставится в соответствие третий элемент z из М, называемый суммой и обозначаемый x+y=z.

2-е. Имеется правило по которому любому элементу х из М и действительному числу к ставится в соответствие элемент у из М, называемый произведением числа на элемент и обозначаемый кx=y.

3-е. Указанные правила подчиняются законам (аксиомам):

1* :

2* ;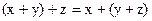

3* существует элемент, называемый нуль элементом и обозначаемый 0, такой, что ;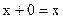

4* для каждого х существует элемент, называемый противоположный и обозначаемый 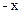, такой что ;

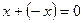5* ;

6* 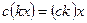– сочетательный закон для умножения;

7* – распределительный закон умножения относительно сложения;

8* - распределительный закон сложения относительно умножения.

Если же природа элементов указана так же как и конкретный вид операций, то множество называют конкретным линейным пространством.

Примеры. Множество всех векторов на прямой (на плоскости, в пространстве), если сложение определено по правилу треугольника (параллелограмма), а умножение на число как деформация, будет линейным векторным пространством с обозначением V₁(V₂, V₃).

Множество полиномов степени не выше 2, если правила суммирования и умножения на число определены как обычно, линейное векторное пространство.

Множество функций, непрерывных на отрезке, множество решений однородной системы и т.д.

В то же время полиномов степени 2, если правила суммирования и умножения на число определены как обычно, не будет линейным векторным пространством, т.к. возможно потеря старшей степени при суммировании таких полиномов (после приведения подобных).

Элементы линейных пространств принято называть векторами. А т.к. умножение производят на действительное число, то еще и действительными.

Определение. Выражение 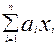принято называть линейной комбинацией элементов (векторов) ЛП.

Определение. Элементы (векторы) {x_i} называют линейно независимыми, если их 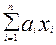обращается в нуль тогда и только тогда, когда все a_i =0.

Определение. Множество {x_i} ненулевых линейно независимых векторов (элементов) называют базисом ЛП, если для любого х не из этого множества существуют такие { a_i } не все равные нулю, что будет справедливо равенство х=.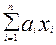

Последнее равенство называют разложением элемента х в базисе(по базису).

Определение. ЛП называют n-мерным, если в нем существуют n линейно независимых вектора, а n+1 вектор уже будут линейно зависимыми. N называют размерность ЛП и записывают это так dimM=n.

Т.к. иных операций в ЛП не введено, то

Определение. Два ЛП называют изоморфными, если между их элементами установлено взаимно-однозначное соответствие ткк, что, если х и у принадлежат ЛП M и им соответствуют x’, y’ из ЛП M’, то х+у соответствует x’+y’, а кх соответствует кx’ из М’.

Из последнего следует, что единственной характеристикой ЛП является его размерность. Пишут так Mn.

Определение. Подмножество L из ЛП М, в котором справедливы указанные в определении ЛП операции называют линейным подпространством из Mn.

Определение. Действительное ЛП называют евклидовым, если выполнены требования:

имеется правило, по которому любым х и у из ЛП ставится в соответствие действительное число, называемое скалярным произведением и обозначаемое (х,у);

указанное правило подчиняется аксиомам: а - (х,у)=(у,х); б – (х₁+х₂)у=х₁у+х₂у; с – (кх,у)=к(х,у) для любого к; d – (х,х)>0, если х не нулевой и (х,х)=0, если х - нулевой.

Примерами евклидова пространства будут уже упоминаемые ранее V₁,V₂, V₃.

Примером ЕП будет множество упорядоченных совокупностей Аn, если операцию скалярное произведение определить по формуле (х,у)= .

Свойства. Для любых х и у из ЕП справедливо равенство (Коши-Буняковсого) (х,у)² 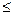(х,х)(у,у).

Доказательство. Согласно аксиомы d имеем (кх-у,кх-у)=к²(х,х)-2к(х,у)+(у,у) 0. Для того, чтобы квадратный трехчлен был неотрицателен при любых значениях переменной к требуется, чтобы дискриминант был неположителен. Получаем (х,у)²-(х,х)(у,у) 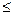0. Откуда и следует требуемое.

Определение. ЛП называют нормированным, если выполнены требования:

имеется правило, по которому любому х из ЛП ставится в соответствие действительное число, называемое нормой элемента и обозначаемое 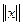(длиной);

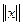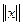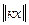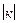
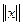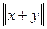
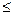
это правило подчиняется аксиомам: а - >0, если х не нуль и =0, если х – нуль-элемент; б - = для любого действительного к; с – для любых х и у верно 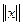+ 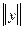- неравенство треугольника.

ЕП будет нормированным, если норму определить так 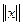=(корень квадратный из скалярного квадрата).

Определение. n – элементов e_i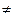0 образуют ортонормированный базис в ЛП, если:

а – (e_i, e_i)= . Получение =1 называют нормированием.

Свойство. Если ЛП ортонормированно с базисом { e_i }, то (х,у)= .

Доказательство. Пусть х и у произвольные из ЕП и { e_i } произвольный ортонормированный в нем. Тогда х=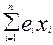 и у=. Но тогда (х,у)= (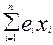,)=, ввиду ортогональности e_i.

Теперь легко выяснить смысл понятия ‘координата’ в ортонормированном базисе. Возьмем произвольный х=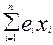 и произвольный e_i из базиса. Вычислим (х, e_i) =(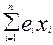, e_i)=x_i. Т.е. координата – это произведение вектора х на базисный орт.

Контрольные вопросы и задания для самостоятельной подготовки:

1. Векторы и их свойства.

2. Скалярное, векторное и смешанное произведение векторов.

3. Линейная зависимость векторов.

4. Размерность и базис векторного пространства.

5. Переход к новому базису.

6. Евклидово пространство.

7. Линейные операторы.

8. Линейное пространство.

9. Декартово пространство.

10. Даны три вектора: 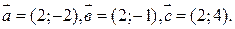Найти координаты вектора .

10. Найти линейную комбинацию векторов 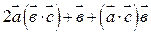если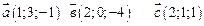

11. Найти линейную комбинацию векторов , если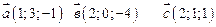

12. Найти линейную комбинацию векторов и угол между векторам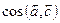и:

, если

13. Найти линейную комбинацию векторов и угол между векторами:

, если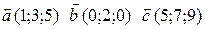

14. Найти линейную комбинацию векторов и угол между векторам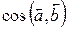и:

, если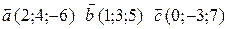

15. Найти линейную комбинацию векторов и угол между векторам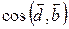и:

, если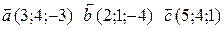

Дата добавления: 2014-10-23