Наращение по простым процентным ставкам

Тесты

Задачи

Вопросы для самостоятельного изучения

1. История возникновения и развития науки финансовая математика.

2. Необходимость проведения финансовых расчетов в условиях рыночной экономики.

3. Время как фактор в финансовых расчетах.

4. Функции процентных ставок.

5. Классификация процентных ставок.

6. Арифметическая и геометрическая прогрессии, формулы определения суммы, элементов и количества членов арифметической и геометрической прогрессий.

1. Выразить следующие проценты в виде соответствующих натуральных и десятичных дробей с точностью до четвертого десятичного знака: a) 5 %, b) 20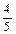%, c) 3,2 %, d) 31,3 %,e) 0,8 %, f)%.

2. Представить каждую из следующих дробей в виде процентов с точностью до сотой доли процента: a) 0,035; b) 3/40; c) 0,04; d) 5/16; e) ; f) .

3. Найти значения 1 + i*t и выразить результат в виде натуральных и десятичных дробей a) i = 6 %, ; b)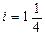%, 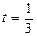; c) i = 5 %, ; d) i = 3.2 %, ; e) i = 3.2%, .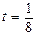

4. Иванов взял в коммерческом банке кредит 10 000 грн. Если банк начисляет 250 грн. за использование этой суммы в течение шести месяцев, то какой будет процентная ставка?

5. Иванов взял в долг у Петрова некоторую сумму денег без процентов и обещал вернуть в течение 11 дней следующим образом: в 1 день - 110 грн., а в последующие дни, уменьшая сумму каждого предыдущего дня на 10 грн..

Определить:

a) сумму, выплаченную Ивановым в последний день;

b) какую сумму Иванов занял у Петрова.

6. Определить срок возврата суммы, взятой без процентов, если стороны договорились, что в первый месяц должник выплатит 10 грн, а в каждый последующий месяц сумма будет возрастать на 5 грн. по сравнению с предыдущим, и в последний месяц составит 80 грн. На какую сумму заключен договор?

7. В течение 10 месяцев на предприятие будут поступать платежи, уменьшающиеся каждый месяц в 0,5 раза. Если последний платеж составит 7 грн. определить:

a) размер первого платежа и общую сумму платежей;

b) размер пятого платежа.

8. Определить первую и последнюю выплату из 8 существующих, если общая сумма выплат составляет 765 грн., а каждая выплата по отношению к предыдущей выплате увеличивается в 2 раза.

9. Банк «Кредит» на вклад, внесенный 23.07 текущего года, начислял следующие годовые проценты: 23.07 – 19 %; с 24.07 по 31.07 – 18,5 %; с 1.08 по 25.08 – 17 %; с 26.08 по 6.09 – 16,5 %; с 7.09 по 13.09 –16 %; с 14.09 по 24.09 – 15 %. Определить среднюю процентную ставку за данный период.

10. Месячные уровни инфляции с февраля по июль текущего года следующие: февраль – 4 %, март – 5 %, апрель – 4.5 %, май –3 %, июнь – 3,5 %, июль –3 %. Определить среднее значение инфляции за указанный период.

11. Клиент разместил три срочных депозита в коммерческих банках на срок 3, 6 и 2 месяца. Процентные ставки соответственно – 14 %, 18 %, 11 %. Определить средневзвешенную процентную ставку.

12. Первоначально цену товара снизили на 10 %, затем - на 15 %, потом еще на 20 %. На сколько всего процентов снизили цену?

Возможно несколько вариантов ответов.

1. Принцип неравноценности денег заключается в том, что:

а) деньги обесцениваются со временем;

b) деньги приносят доход;

c) равные по абсолютной величине денежные суммы, относящиеся к различным моментам времени, оцениваются по-разному;

d) сегодняшние деньги ценнее завтрашних денег.

2. Финансово-коммерческие расчеты используются для:

a) определения выручки от реализации продукции;

b) расчета кредитных операций;

c) расчета рентабельности производства;

d) расчета доходности ценных бумаг.

3. Подход, при котором фактор времени играет решающую роль, называется:

a) временной;

b) статический;

c) динамический;

d) статистический.

4. Проценты в финансовых расчетах:

a) доходность, выраженная в виде десятичной дроби;

b) абсолютная величина дохода от предоставления денег в долг в любой его форме;

c) показывают, сколько денежных единиц должен заплатить заемщик за пользование в течение определенного периода времени 100 единиц первоначальной суммы долга.

5. Процентная ставка – это:

a) относительный показатель, характеризующий интенсивность начисления процентов;

b) абсолютная величина дохода от предоставления денег в долг в любой его форме;

c) ставка, зафиксированная в виде определенного числа в финансовых контрактах;

d) отношение суммы процентных денег к величине ссуды.

6. В качестве единицы времени в финансовых расчетах принят:

a) год;

b) квартал;

c) месяц;

d) час.

7. Виды процентных ставок в зависимости от исходной базы:

a) постоянная, сложная;

b) простая, переменная;

c) простая, сложная;

d) постоянная, переменная.

8. Фиксированная процентная ставка – это:

a) ставка, неизменная на протяжении всего периода ссуды;

b) ставка, применяемая к одной и той же первоначальной сумме долга;

c) ставка, зафиксированная в виде определенного числа в финансовых контрактах;

d) отношение суммы процентных денег к величине ссуды.

Наращением или ростом называется процесс увеличения некоторой суммы денег за счет начисления не нее процентов. Под наращенной суммой понимают первоначальную сумму с начисленными процентами к концу срока начисления.

Существует два принципа расчетов процентных денег:

а) от настоящего к будущему с применением ставки наращения, - декурсивные проценты;

б) от будущего к настоящему с применением учетных или дисконтных ставок, - антисипативные проценты.

В зависимости от способа начисления, проценты делятся на простые и сложные.

Простые проценты - это метод начисления, при котором сумма процентов определяется в течение всего периода, исходя из первоначальной величины долга, независимо от количества периодов начисления и их длительности. Простые проценты по декурсивному методу начисляются по формуле:

,

где PV – первоначальная,текущая стоимость (англ. present value) – исходная сумма долга или оценка современной величины денежной суммы, поступление которой ожидается в будущем, в пересчете на более ранний момент времени;

FV – наращенная, будущая стоимость (англ. future value) – сумма долга с начисленными процентами в конце срока;

i – ставка процента(англ. rate of interest) является относительным показателем эффективности вложений (норма доходности), характеризующим темп прироста стоимости за период;

n – срок погашения долга (англ. number of periods) – интервал времени, по истечении которого сумму долга и проценты нужно вернуть.

Пример 1. Вкладчик положил в банк, выплачивающий 18 % годовых. сумму 1000 грн. Какая сумма будет на счете через год?

Решение. По формуле наращения по простой процентной ставке:

грн.

Следовательно, через год на счету будет сумма 1180 грн.

Если срок финансовой операции не равен целому числу лет, то срок операции n определяем следующим образом:

где t – число дней финансовой операции,

K – временная база начисления процентов.

При расчете процентов используют две временные базы: K=360 дней или K=365, 366 дней. Число дней операции определяется приближенно или точно. Точное число дней между датой выдачи и датой погашения можно определить по таблице приложения А. Варианты расчета срока финансовой операции представлены в таблице 2.1.

Таблица 2.1 – Расчет срока финансовой операции

Варианты расчета	Определение срока финансовой операции	Временная база	Примечание
Точные проценты	Точное число дней операции	365 или 366	Английская практика расчетов
Обыкновенные проценты с точным числом дней	Точное число дней операции		Французская практика расчетов
Обыкновенные проценты с приближенным числом дней	Приближенное число дней, исходя из условия, что в каждом месяце 30 дней		Германская практика расчетов

Пример 2. Ссуда в размере 10000 грн. выдана 25.01 по 8.08 этого же не високосного года под 17 % простых годовых. Определить сумму, которую должен заплатить должник в конце срока, используя три методики расчета

Решение:

1. Определяем число дней операции:

точное число дней – (7+28+31+30+31+30+31+8-1)=195

приближенное число дней – (7+30+30+30+30+30+30+8-1)=194

2. Точные проценты с точным числом дней операции

грн.

3. Обыкновенные проценты с точным числом дней операции

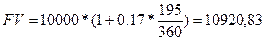грн.

4. Обыкновенные проценты с приближенным числом дней операции

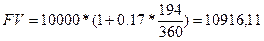грн.

Таким образом, должнику необходимо заплатить в конце срока следующие суммы: по методу точных процентов – 10908,22 грн, по методу обыкновенных процентов с точным числом дней операции -10920,83 грн., по методу обыкновенных процентов с приближенным числом дней операции – 10916,11 грн.

Если договором предусмотрено изменение процентной ставки во времени, то наращенная сумма определяется следующим образом:

,

где - ставка простых процентов в периоде

Пример 3. Вклад в сумме 5000 грн. был положен в банк 25 мая не високосного года по ставке 18 % годовых, а с 1 июля банк снизил ставку по вкладам до 16 % годовых и 15 июля вклад был востребован. Определить сумму начисленных процентов по английской практике начисления.

Решение:

1. Количество дней для начисления процентов по первоначально действующей процентной ставке в размере 18 % годовых рассчитывается точно и составляет 37 дней, а по измененной ставке 16 % годовых – 14 дней.

2. Начисленные проценты:

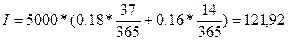грн.

Таким образом, при закрытии счета клиент должен получить процентов в сумме 121,92 грн.

Кроме процентной ставки, существует учетная ставка (или ставка дисконта) d, которая равна отношению процентного дохода к конечной сумме. Начисление процентов с применением ставки дисконта называется антисипативным методом. Наращенная сумма в этом случае равна:

,

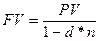где d – учетная ставка.

Пример 4. Застройщи к желает получить ссуду в кредитном учреждении на 6 месяцев. Если кредитное учреждение начисляет проценты авансом по ставке 17 %, какую сумму должен просить застройщик, чтобы получить на руки 10000 грн.

Решение:

По методу антисипативных процентов находим наращенную сумму:

грн.

Итак, для получения на руки 10000 грн. при начислении процентов авансом, ссуда должна быть в сумме 10928,96 грн.

Формула для определения простой ставки процентов, компенсирующей ожидаемую инфляцию, имеет следующий вид:

i_τ = [(1 + i*n)* J_τ - 1]: n,

где i – простая ставка процентов;

i _τ – процентная ставка с поправкой на инфляцию;

J_r – индекс инфляции.

Пример 5. Банк выдал клиенту кредит на один год в размере 20 000 грн. по ставке 18 % годовых. Уровень инфляции за год составил 9 %. Определить с учетом инфляции реальную ставку процентов по кредиту, погашаемую сумму и сумму процентов за кредит.

Решение:

1. Номинальная наращенная сумма

FV = PV* (1 + i * n) = 20000* (1 + 0,18) = 23600 грн.

Номинальные начисленные проценты

I = FV - PV = 23600 - 20000 = 3600 грн.

2. Реальная наращенная сумма

FV_τ = FV / (1 + h) = 23600 / 1,09 = 21651,3 грн.

Реальные проценты

I_τ = FV_τ - PV = 21651,3 - 20000 = 1651,3 грн.

Таким образом, реальные проценты меньше номинальных начисленных процентов.

3. Ставка по кредиту с учетом инфляции должна быть равна

i_τ = [(1 + i * n)* I _τ - 1]: n = (1,18 * 1,09 - 1) / 1 = 0,286

Наращенная сумма

FV = PV* (1 + i * n) = 20000 (1 + 0,286) = 25720 грн.

Доход банка

I = FV - PV = 25720 - 20000 = 5720 грн.

4. Реальный доход банка

I_τ = FV_τ - PV = 25720 / 1,09 - 20000 = 3596,3 грн.

Реальная доходность финансовой операции

i = I_τ / PV = 3596,3 / 20000 = 0,18

Таким образом, чтобы обеспечить доходность в размере 18 % годовых, ставка по кредиту с учетом инфляции должна соответствовать 28,6 % годовых.

Дата добавления: 2014-10-31