Какой из ниже перечисленных способов измерения времени при расчете процентного дохода не используется на практике?

Тесты

Задачи

Вопросы для самостоятельного изучения

1. Формула наращения по простым процентам.

2. График наращения по простым процентам.

3. Экономический смысл множителя наращения по простым процентам.

4. Начисление процентов при изменении сумм депозита во времени.

5. Основные финансовые операции использования схемы простых процентов.

6. Наращение процентов в потребительском кредитовании.

7. Определение срока операции и процентной ставки.

1. Депозитный счет в размере 4000 грн. открыт в коммерческом банке на 3 месяца под 17 % годовых. Найти процентный доход, который получит вкладчик при начислении простых процентов.

2 Молодая семья получила в банке ссуду на строительство жилья в размере 60 000 грн. сроком на 3 года под простую процентную ставку 20 % годовых. Определите наращенную сумму кредита и сумму уплаченных процентов.

3. Банк принимает вклады на срочный депозит на следующих условиях: процентная ставка при сроке 35 дней – 14.5 %; при сроке 65 дней – 16 %; при сроке 90 дней –18 %. Рассчитайте доход клиента при вкладе 10 000 грн. на указанные сроки. Год не високосный. Методика расчета: точные проценты с точным числом дней.

4. Клиент внес в банк на депозитный счет 2000 грн на срок с 12 апреля по 26 июня на условиях простой процентной ставки 16 % годовых. Рассчитайте доход клиента по трем методикам. Год не високосный.

5 Коммерческий банк привлекает средства населения под простые проценты 20 % годовых. Клиент внес 6 000 грн. на депозит с 12 февраля по 24 апреля. Определите величину коэффициента наращения и наращенную сумму для случая: а) точных процентов с точным числом дней; в) обыкновенных процентов с приближенным числом дней. Год не високосный.

6. Клиент внес на депозитный счет в банк сроком на 6 месяцев 3000 грн. Согласно условиям договора, процентная ставка может быть изменена банком в одностороннем порядке. Вклад внесен 3 апреля под 24 % годовых, 22 апреля процентная ставка, согласно решению Правления банка, установлена в 22 % годовых, а 1 сентября – 21,5 % годовых. Определите сумму на счете и процентный доход при закрытии счета, если расчет процентов производится по точным процентам с точным числом дней в году.

7. Найти, в течении какого количества лет вклад в размере 1500 грн. возрастет до 3000 грн. при начислении процентов по простой ставке 15 % годовых.

8. Вкладчик собирается положить в банк сумму 15000 грн. с целью накопления 16500 грн. Ставка процентов будет составлять 21 % годовых. Найти срок в днях, за который вкладчик сможет накопить требуемую сумму. Необходимо учесть, что банк использует при расчетах фактическое значение количества дней в году и временная база 365 дней.

9. Клиент, решивший внести на депозит 2000 грн., хочет накопить через год не менее 2700 грн. Необходимо найти требуемую простую ставку процентов, на основании которой он может выбрать банк для размещения своих средств.

10. Имеются две суммы денег, одна больше другой на 500 грн. большая сумма вложена на 6 месяцев при ставке 12 % годовых. меньшая сумма внесена на 3 месяца при ставке 15 % годовых. процентный доход за большую сумму вдвое больше процентного дохода за меньшую сумму. Необходимо найти величину этих денежных сумм.

11. На какой временной период должен быть вложен капитал при 12 % простых годовых, чтобы процентный доход был равен тройной сумме капитала?

12. Ссуда в размере 15 000 грн. выдается на полгода под 20 % годовых. Найти сумму начисленных процентов по простой ставке декурсивным и антисипативным методами. Сделать вывод, какой метод более выгоден заемщику, кредитору.

13. Вкладчик внес 5000 грн. с целью накопления 7000 грн. Определить срок в днях, за который вкладчик накопит требуемую сумму по декурсивному и антисипативному методу начисления простых процентов. Процентная ставка банка – 14 % годовых.

14. Заполните в таблице пропущенные клетки, если используется вариант начисления точных процентов, год не високосный

Проценты, грн.	Первоначальная сумма, ден.ед..	Ставка процентов, %	Срок
23,6	?	15,50 %	18.02-27.05
960,17	?	16 %	17.02-11.04
370,6	?	18 %	6.05-10.10
45,6		?	28.02-11.04
30,2		?	9.09-17.12
70,5		?	11.05-4.11
11,73		16 %	?
28,6		20 %	?
9,13		17 %	?

15. При открытии счета 10.12.2007 г. клиентом была внесена сумма в размере 5000 грн. под 16,5 % годовых. 1.02.2008 г. на счет добавлено 1500 грн., 10.02.2008 г. еще внесено 1400 грн. Вкладчик хочет закрыть счет 7.10.2008 г. Сколько денег получит вкладчик при закрытии счета, если календарная база определяется по французской практике?

16. При уровне инфляции 5 % банк выдает кредит 25 000 грн.. на 100 дней. Простая процентная ставка – 18 %. Определить процентную ставку, которая учитывает инфляцию, и сумму погашающего платежа с учетом инфляции, используя французскую практику расчетов.

17. Уровень инфляции – 10 %. Банк выдает кредит 60000 грн. на 120 дней с простой процентной ставкой – 25 %. Определить процентную ставку, которая учитывает инфляцию и сумму погашающего платежа с учетом инфляции, используя английскую практику расчетов.

18. Имеются два обязательства. Условия первого: по окончанию срока операции 4 месяца - сумма 3000 грн., условия второго: по окончанию срока операции 9 месяцев - сумма 3600 грн.. Определить: а) ставку простого процента, при которой эти обязательства равноценны; б) какое из этих обязательств выгоднее для получателя денег при ставке простых процентов 20 %.

Возможно несколько вариантов ответов

1. Наращение – это:

a) процесс увеличения капитала за счет присоединения процентов;

b) базисный темп роста;

c) отношение наращенной суммы к первоначальной сумме долга;

d) движение денежного потока от настоящего к будущему.

2. Коэффициент наращения – это:

a) отношение суммы процентных денег к величине первоначальной суммы;

b) отношение наращенной суммы к первоначальной сумме;

c) отношение первоначальной суммы к будущей величине денежной суммы;

d) отношение процентов к процентной ставке.

3. Если число дней финансовой операции определяется исходя из того, что в каждом месяце 30 дней, то такой метод начисления называется:

a) точные проценты с точным числом дней операции;

b) обыкновенные проценты с точным числом дней операции;

c) обыкновенные проценты с приближенным числом дней.

4. Формула наращения по простой учетной ставке

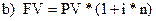5. Формула наращения простых процентов:

a) FV = PV * i * n

b) FV = PV* (1 + i) ⁿ

c) FV = PV* (1 + i * n)

d) FV = PV* (1 + i)

6. Точное число дней финансовой операции можно определить:

a) по специальным таблицам порядковых номеров дней года;

b) используя прямой счет фактических дней между датами;

c) исходя из продолжительности каждого целого месяца в 30 дней;

d) считая дату выдачи и дату погашения ссуды за один день.

7. Французская практика начисления процентов:

a) обыкновенный процент с приближенным числом дней финансовой операции;

b) обыкновенный процент с точным числом дней финансовой операции;

c) точный процент с точным числом дней финансовой операции;

d) точный процент с приближенным числом дней финансовой операции.

8. Германская практика начисления процентов:

a) обыкновенный процент с приближенным числом дней финансовой операции;

b) обыкновенный процент с точным числом дней финансовой операции;

c) точный процент с точным числом дней финансовой операции;

d) точный процент с приближенным числом дней финансовой операции

9. Английская практика начисления процентов:

a) обыкновенный процент с приближенным числом дней финансовой операции;

b) обыкновенный процент с точным числом дней финансовой операции;

c) точный процент с точным числом дней финансовой операции;

d) точный процент с приближенным числом дней финансовой операции

a) год - 360 дней, месяц - 30 дней;

b) год - 365 дней, месяц - 30 дней;

c) год - 360 дней, месяц - точное число дней;

d) год -365 дней, месяц - точное число дней.

11. Расчет наращенной суммы в случае дискретно изменяющейся во времени процентной ставки по схеме простых процентов имеет следующий вид:

a) FV = PV *(1 + Σ n_кi_к);

b) FV = PV *Σ (1 + n_кi_к);

c) FV = PV* (1 + n ₁ i ₁)*(1 + n ₂ i ₂)*….* (1 + n_кi_к);

d) FV = PV* (1 + n i_к).

12. Срок финансовой операции по схеме простых процентов определяется по формуле:

a) n = I / (PV*• i);

b) n = [(FV - PV) / (FV * t)]* i;

c) t = [(FV - PV) / (PV * i)] * K;

d) n = [(FV - PV) / (FV * t)]* K;

13. Если в условиях финансовой операции отсутствует простая процентная ставка, то:

a) этого не может быть;

b) процентную ставку можно определить по формуле

i = [(FV - PV) / (PV * t)]* K;

c) алгебраического определения процентной ставки не существует;

d) процентную ставку можно определить по формуле

i = Σ процентных чисел / процентный делитель

14. Процентная ставка финансовой операции по схеме простых процентов определяется по формуле:

a ) i = I / (PV*• n)

b ) i = [(FV - PV) / (P V * n)]

c ) i = [(FV - PV) / (PV * t)] * K

d) i = [(FV - PV) / (FV * t)]* K

15. Если номинальная процентная ставка составляет 10%, а темп инфляции определен в 9% в год, то реальная процентная ставка составит:

a) 19 %;

b) 18 %;

c) 19,9 %;

d) – 6 %;

e) 24 %.

Дата добавления: 2014-10-31