Наращение по сложным процентным ставкам

Сложные проценты – это метод начисления, при котором сумма начисленных в каждом расчетном периоде процентов прибавляется к сумме капитала на начало расчетного периода и в следующем расчетном периоде начисление процентов производится на уже наращенную сумму. Процесс наращения некоторой суммы по сложным процентам называется капитализацией. Сложные проценты по декурсивному методу начисляются по формуле:

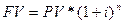, (3.1)

где (1+ i)ⁿ - коэффициент или множитель наращения. Для облегчения расчетов можно пользоваться таблицами коэффициентов наращения сложных процентов, которые приведены в приложении Б.

Пример 1. Банк ежегодно начисляет 18 % сложных. Клиент положил в банк 20000 грн. Какая сумма будет на счете через: а) 4 года; б) 5 лет и 3 месяца?

Решение:

По формуле (3.1) находим сумму, которая будет на счете клиента.

а) 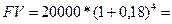38775,56 грн;

б) срок операции n = 5,25 лет

FV =20000*(1+0,18)^5.25= 47688,16 грн.

Таким образом, на счете клиента через 4 года будет сумма 38775,56 грн, через 5 лет и 3 месяца – 47688,16 грн.

В случае использования переменных процентных ставок, формула наращения имеет следующий вид:

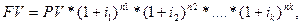(3.2)

где i_k – последовательные значения процентных ставок в соответствующие периоды времени n_k.

Пример 2. Фирма получила кредит в банке на сумму 10000 грн. сроком на 5 лет. Процентная ставка по кредиту определена в 17 % для 1-го года, для 2-го года предусмотрена надбавка к процентной ставке в размере 1,5 %, для последующих лет 1 %. Определить сумму долга, подлежащую погашению в конце срока займа.

Решение:

Используя формулу наращения сложных переменных процентных ставок (3,2):

FV = 10000 * (1 + 0,17) * (1 + 0,185) * (1+0,195)³ = 23659,63 грн.

Таким образом, сумма, подлежащая погашению в конце срока займа, составит, 23659,63 грн., из которых 10000 грн. являются непосредственно суммой долга, а 13659,63 грн. – проценты по долгу.

Период начисления процентов по сложным процентам не всегда равен году, однако в условиях финансовой операции указывается не ставка за период, а годовая ставка с указанием периода начисления – номинальная ставка. Ф ормула сложных процентов при начислении процентов чаще одного раза в год имеет следующий вид:

FV=PV *(1 + j / m)^n*m, (3.3)

где j – номинальная годовая ставка процентов,

m – число периодов начисления процентов в году.

Пример 3. Сумма в размере 20000 грн. дана в долг на 4 года по ставке процента равной 18 % годовых с ежеквартальным начислением процентов. Определить проценты и сумму, подлежащую возврату.

Решение:

Наращенная сумма, рассчитанная по формуле (3.3) составит:

FV =20000 *(1+0,18/4)^4*4= 40447,4 грн.

Проценты найдем по формуле:

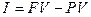=40447,4-20000=20447,4 грн.

Таким образом, через 4 года необходимо вернуть сумму в размере 40447,4 грн., из которой 20000 грн. является первоначальной суммой, взятой в долг, а 20447,4 грн. – сумма начисленных процентов.

Эффективная ставка измеряет тот реальный относительный доход, который получен в целом за год, с учетом внутригодовой капитализации. Эффективная ставка показывает, какая годовая ставка сложных процентов дает тот же финансовый результат, что и наращение m в год по ставке j:

(1 + i) ⁿ = (1 + j / m) ^{m * n},

следовательно,

i =(1+ j / m) ^m - 1. (3.4)

Пример 4. Рассчитаем эффективную ставку для финансовой операции, рассмотренной в предыдущем примере, а также для вклада при ежемесячном начислении процентов по годовой ставке 18 %.

Решение:

Эффективная ставка ежеквартального начисления процентов, исходя из 18% годовых, составит:

i = (1 + j / m) ^m - 1 = (1 + 0,18 / 4)⁴ - 1 = 0,1925=19,25 %.

Эффективная ставка ежемесячного начисления процентов будет равна:

i = (1 + j / m) ^m - 1 = (1 + 0,18 / 12)¹² - 1 = 0,1956=19,56 %.

Таким образом, годовая ставка, эквивалентная номинальной ставке процентов в размере 18 % годовых при ежемесячном начислении процентов, составит 19,56 % против 19,25 % с ежеквартальным начислением процентов. Чем больше периодов начисления, тем быстрее идет процесс наращения.

На практике, а чаще всего в теории, встречаются случаи, когда проценты начисляются непрерывно, за сколь угодно малый промежуток времени. Формула наращенной суммы при непрерывном начислении процентов имеет следующий вид:

FV=PV e ^{j * n} = P * e ^{δ * n}, (3.5)

где e ≈ 2,718281, называется числом Эйлера;

δ - ставка непрерывных процентов или сила роста..

Пример 5. Кредит в размере 10000 грн. получен сроком на 3 года под 20 % годовых. Определить сумму подлежащего возврату в конце срока кредита, если проценты будут начисляться:

а) один раз в год;

б) ежедневно;

в) непрерывно.

Решение:

Используем формулы дискретных и непрерывных процентов:

а) начисление один раз в год:

FV = 10000 * (1 + 0,2)³ = 17289 грн.

б) ежедневное начисление процентов:

FV = 10000 * (1 + 0,2 / 365)^{365*• 3} = 18218,19 грн

в) непрерывное начисление процентов:

FV = 10000 * e^{0,2 • 3} = 18221,18 грн

Таким образом, возврату за кредит подлежат суммы в 17289 грн. при ежегодном начислении процентов, 18218,19 грн. – при ежедневном начислении процентов, 18221,18 грн – при непрерывном начислении процентов.

Начисление процентов по сложной учетной ставке или по антисипативному методу осуществляется по следующим формулам:

а) если проценты начисляются один раз в год

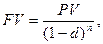(3.6)

б) если проценты чаще одного раза в год

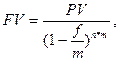(3.7)

где f – номинальная годовая учетная ставка.

Формула для определения сложной ставки процентов, компенсирующей ожидаемую инфляцию, имеет следующий вид:

i_τ = i + h + i*h.

где h – уровень инфляции

Пример 6. Определить номинальную ставку процентов для финансовой операции, если уровень эффективности должен составлять 17 % годовых, а годовой уровень инфляции 9 %.

Решение:

Процентная ставка с учетом инфляции

i_τ = i + h + i*h = 0,17 + 0,09 + 0,17 • 0,09 = 0, 2753=27,53 %.

Таким образом, номинальная ставка должна составить 27,53 %. чтобы обеспечить реальную эффективность в 17 %.

Для расчета продолжительности финансовых операций и уровня процентных ставок можно воспользоваться формулами, приведенными в приложении В.

Дата добавления: 2014-10-31