Может ли современная величина годовой ренты быть меньше ее годового платежа?

Тесты

Задачи

Вопросы для самостоятельного изучения

1. Виды потоков платежей и их основные параметры.

2. Классификация финансовых рент.

3. Параметры финансовых рент.

4. Вечная рента.

5. Параметры рент пренумерандо.

6. Определение параметров постоянных рент при известной наращенной сумме.

7. Определение параметров постоянных рент при известной современной стоимости.

1. Финансовая рента состоит из kравных по величине платежей R, которые следуют с периодичностью r лет (r > 1). Сложные проценты по ставке i начисляются один раз в год. Первая выплата производится в конце года r. Определить:

а) современную величину и наращенную сумму ренты;

б) как изменятся эти характеристики при условии, что платежи осуществляются в начале каждого периода?

2. Клиент вкладывает 2500 грн. в конце каждого года в банк, выплачивающий проценты по ставке 18 % сложных годовых. Определить, какая сумма будет на счете клиента: а) через 3 года, б) через 10 лет?

3. Господин Сидоров хочет накопить за 6 лет 40000 грн., осуществляя: а) ежегодные, б) ежеквартальные, в) ежемесячные равные вклады в банк, который выплачивает проценты по ставке 18 % годовых (сложных). Определить, какие взносы должен осуществлять господин Сидоров?

4. Предприятие создаёт фонд для постройки нового здания, вкла­дывая в него каждые 4 года 15000 грн. Для создания фонда в банке открыт депозитный счет, по которому начисляются проценты по ставке: а) 16 % сложных годовых, б) j4 = 16 % годовых. Какая сумма будет в фонде через 16 лет?

5. Банк выплачивает по депозитному вкладу проценты по ставке j₄ = 24 %. Клиент вкладывает в этот банк ежегодно 800 грн., осуществляя равные вклады: а) в конце каждого квартала, б) ежемесячно. Какая сумма будет на счету этого клиента через 5 лет?

6. Банк по депозитному вкладу начисляет непрерывные проценты по ставке (силе роста) d = 18 %. Клиент вкладывает в этот банк в конце каждого года 5000 грн. Определить, какая сумма будет на его счете через 7 лет?

7. Текущая стоимость обычной ренты со взносами размером 650 грн. в конце каждого месяца и начислением 14 % годовых один раз в год равна 20000 грн. Определить срок ренты и наращенную сумму.

8. Фирма создает резервный фонд и для этого ежемесячно переводит в банк 8000 грн. Годовая процентная ставка при начислении процентов один раз в год – 16 %. Определить, через какое время на счете фирмы будет 30000 грн.?

9. Пенсионер хочет купить аннуитет, по которому он будет получать в конце года 4000 грн. По статистическим расчетам страховой компании продолжительность жизни для возраста пенсионера 25 лет. Процент по аннуитету, предлагаемый компанией, равен 18 % годовых. Определить, какую сумму пенсионер должен заплатить за этот аннуитет.

10. Наращенная стоимость срочной ренты с ежемесячными взносами в начале каждого месяца по 800 грн. и ежемесячным начислением процентов равна 40000 грн. Номинальная годовая процентная ставка – 24 %. Определить срок ренты.

11. Пенсионер вкладывает в начале каждого месяца в банк по 50 грн. под 16 % годовых. Определить, через какое время он накопит сумму, достаточную для покупки холодильника стоимостью 3000 грн. Проценты начисляются ежемесячно.

12. Инвестор покупает нефтеносный участок, который будет приносить в течение 20 лет доход 5000 грн. ежеквартально, по­сле чего запасы нефти истощатся, а участок не будет представлять ценности. Инвестор желает получать 12 % ежегодного дохода на вложенную сумму. Определить, какую максимальную сумму инвестор может заплатить за участок.

13. Пенсионер собирает деньги на покупку холодильника стоимостью 3000 грн.. Для этого он хочет осуществлять ежемесячные взносы на депозитный счет в банке, который начисляет проценты по ставке 20 % годовых с ежемесячной капитализацией. Определить минимальный ежемесячный взнос для накопления требуемой суммы за 2 года.

14. Сумма инвестиций, осуществленных за счет привлеченных средств, равна 180 000 грн.. Предполагается, что отдача от них составит 50 000 грн. ежегодно получаемых в конце года. Определить:

а) за какой срок окупятся инвестиции, если на долг начисляются проценты по ставке 18 % годовых;

б) как следует изменить финансовый поток, чтобы в случае дробного ответа скорректировать срок окупаемости на наименьшее целое число лет, не превосходящее срока окупаемости инвестиции.

15. Перед выходом на пенсию г-н Фёдоров хочет обеспечить себе ежегодный доход неограниченно долго в сумме 5000 д.ед.: а) ежеквартально, б) ежемесячно. Определить, какую сумму он должен положить для этого на депозитный вклад при капитализации 17 % годовых?

16. Владелец дома планирует произвести через 5 лет капитальный ремонт, на который ему потребуется 120000 грн. Он хочет ежегодно вносить на депозитный вклад для этой цели 6000 грн. Определить какая минимальная процентная ставка должна быть на депозитный вклад, чтобы накопить необходимую сумму?

17. Отец собирается положить на депозитный вклад своего сына 18000 грн., чтобы тот в течение 5 лет учёбы в университете мог снимать в конце каждого месяца со счёта 400 грн., исчерпав весь вклад к концу учёбы. Определить, какая минимальная процентная ставка обеспечит данную операцию.

18. Сравниваются два варианта строительства некоторого объекта. Первый требует разовых вложений в сумме 600 000 грн. и капитального ремонта стоимостью 50000 грн. каждые 2 года. Для второго затраты на создание равны 700 000 грн., на капитальный ремонт – 40000 грн. каждые 3 года. Расчет производится на 12 лет. Какой вариант окажется предпочтительнее при условии, что прогнозируемая ставка процента:

а) не превысит 15 %;

б) не опустится ниже 20 %.

19. Организация получила кредит стоимостью 90000 грн. на 1 год. Годовая процентная ставка за пользование кредитом 24 % годовых. Платежи по кредиту осуществляются ежемесячно в начале месяца равными суммами. Определить величину месячного платежа.

20. Найти наращенную сумму и современную стоимость аннуитета, выплачивающего 3000 грн. в конце каждого года в течение 5 лет, если начисление процентов осуществляется с использованием силы роста 15 % годовых.

21. Оформляется контракт, по которому выплачивается 500 грн. в конце каждого полугодия в течение 7 лет и дополнительно 2000 грн. в конце этого срока. Определить, чему равна современная стоимость контракта, если деньги стоят 17 % годовых?

22. Страховой полис подразумевает платежи 700 грн в начале каждого квартала в течение 25 лет и выплатит 10000 грн в случае смерти страхователя. Сколько времени должна продолжаться жизнь страхователя, чтобы компания не разорилась при стоимости денег 14 % эффективно?

23. Клиент изъявил желание каждые три месяца вносить 2000 грн. на депозитный счет. Необходимо найти, когда это более выгодно делать, в начале или в конце квартала. Следует учесть, что банк начисляет сложные проценты в размере 24 % годовых ежеквартально. Срок хранения вклада 1 год.

24. Фирмой предусматривается создание в течение трех лет фонда развития. Фирма имеет возможность ассигновать на эти цели ежквартально 15000 грн., помещая их в банк под 20 % годовых, Какая сумма потребовалась бы фирме для создания фонда такого же размера, если бы она поместила денежные средства в банк на три года под 20 % годовых?

25. Земельное хозяйство стоит 800000 грн. Фермер платит 50000 грн. наличными и будет выплачивать оставшийся долг в течение следующих 10 лет равными платежами ежемесячно. Определить, какими будут эти платежи, если при операции используется процентная ставка 23 % годовых.

26. Оценить с помощью модели постоянной годовой финансовой ренты пренумерандо на 01.01 текущего года наращенную сумму платежей 10000 грн. от 01.01.2005 г. и 11000 грн от 01.01.2006 г., если платежи обеспечивают доходность 20 % годовых.

Возможно несколько вариантов ответов

1. Поток платежей - это:

a) рост инвестированного капитала на величину процентов;

b) распределенные во времени выплаты и поступления;

c) перманентное обесценивание денег;

d) платеж в конце периода.

2. Вечная рента - это:

a) рента, подлежащая безусловной выплате;

b) рента с выплатой в начале периода;

c) рента с бесконечным числом членов;

d) рента с неравными членами.

3. Аннуитет - это:

a) частный случай потока платежей, когда члены потока только положительные величины;

b) частный случай потока платежей, когда число равных временных интервалов ограничено;

c) частный случай потока платежей, когда члены равны и имеют одинаковую направленность, а периоды ренты одинаковы.

4. Финансовая рента называется постоянной, если ее члены:

a) изменяются во времени согласно арифметической прогрессии;

b) изменяются во времени с постоянным относительным приростом;

c) равны между собой;

d) изменяются во времени нерегулярно;

e) изменяются во времени с постоянным абсолютным приростом.

5. Финансовая рента называется р-срочной, если платежи по ней выплачиваются:

a) один раз в год;

b) р раз за весь срок финансовой операции;

c) вечно;

d) р раз на протяжении года;

e) в начале каждого года;

6. Под наращенной суммой финансовой ренты понимают:

a) сумму всех ее членов;

b) сумму всех ее членов, дисконтированных на начало срока ренты или некоторый упреждающий момент времени;

c) сумму всех ее членов с начисленными на них к концу срока ренты процентами;

d) сумму всех ее членов, дисконтированных на начало срока ренты;

e) общую сумму накопленной задолженности.

7. Наращенная величина годовой постоянной обычной ренты определяется по формуле:

a)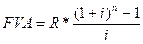

b)

c) 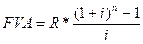* (1+i)

d) *(1+i)

8. Наращенная сумма годовой ренты пренумерандо рассчитывается по формуле:

a);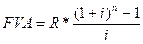

b) ;

c) 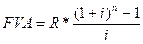* (1+i);

d) *(1+i).

9. Современная величина годовой обычной ренты определяется по формуле:

a) ;

b) ;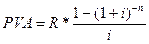

c) *(1+i);

d) 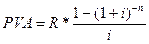*(1+i).

10. Современная величина годовой ренты пренумерандо определяется по формуле:

a) ;

b) ;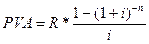

c) *(1+i);

d) 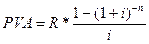*(1+i).

11. Для определения члена ренты необходимо знать:

a) наращенную сумму;

b) первоначальную сумму;

c) первоначальную или наращенную сумму;

d) процентную ставку;

e) срок ренты.

12. Для оценки бессрочного аннуитета не имеет смысла определение:

a) современной величины аннуитета;

b) наращенной величины аннуитета;

c) члена ренты.

13. Верно ли утверждение, что наращенная сумма вечной годовой ренты бесконечна?

a) да;

b) нет.

14. Если платежи по ренте производятся в начале временных периодов, то рента называется:

a) постнумерандо;

b) пренумерандо.

a) да;

b) нет.

16. В потоке платежей разрешается переставлять платежи произвольным образом. Как их надо переставить, чтобы современная величина потока была наибольшей:

a) в порядке возрастания;

b) в порядке, который дает наименьшую наращенную сумму;

c) в порядке, который дает наибольшую наращенную сумму;

d) в порядке убывания.

Дата добавления: 2014-10-31