
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Интервалы выпуклости и вогнутости. Точки перегиба 2 страница
|
|
|
|
Вариант 8
1. Найти обратную матрицу 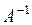 , если
, если 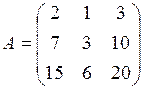 .
.
2. Решить систему линейных уравнений по формулам Крамера:
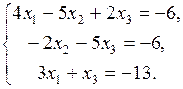
3. Даны две точки 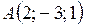 ,
, 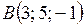 . Найти координаты вектора
. Найти координаты вектора 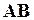 и координаты точки
и координаты точки 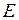 – середины отрезка
– середины отрезка 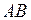 .
.
4. Записать уравнение плоскости 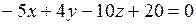 в «отрезках по осям».
в «отрезках по осям».
5. Вычислить пределы:
а)  ; ;
| б) 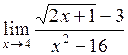 ; ;
|
в) 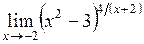 ; ;
| г)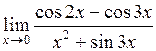 . .
|
6. Вычислить производную 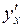 :
:
а)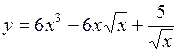 ; ;
| б) 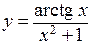 ; ;
|
в)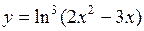 ; ;
| г) 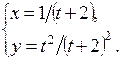
|
7. Вычислить предел, применяя правило Лопиталя:
а) 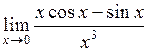 ; ;
| б) 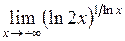 . .
|
8. Найти интервалы выпуклости (вогнутости) функции 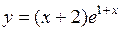 .
.
Ответы: 1. 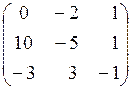 . 2. (–5; –2; 2). 3.
. 2. (–5; –2; 2). 3. 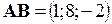 ,
, 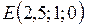 . 4.
. 4. 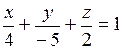 . 5. а) 1/2; б) 1/24; в)
. 5. а) 1/2; б) 1/24; в) 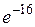 ; г) 0. 7. а) –1/3; б) 1. 8. выпукла на
; г) 0. 7. а) –1/3; б) 1. 8. выпукла на 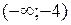 , вогнута на
, вогнута на 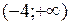 .
.
Вариант 9
1. Найти значение многочлена 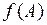 , если
, если 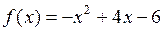 ,
, 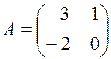 .
.
2. Решить систему линейных уравнений методом Гаусса:
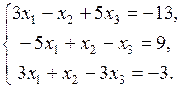
3. Проверить, будут ли векторы 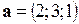 ,
, 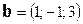 ,
, 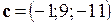 компланарны.
компланарны.
4. Найти угол между плоскостями 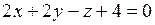 и
и 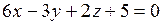 .
.
5. Вычислить пределы:
а) 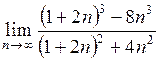 ; ;
| б) 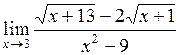 ; ;
|
в) 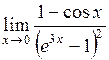 ; ;
| г) 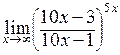 . .
|
6. Вычислить производную 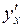 :
:
а) 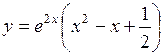 ; ;
| б) 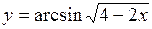 ; ;
|
в) 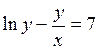 ; ;
| г) 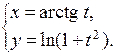
|
7. Вычислить предел, применяя правило Лопиталя:
а) 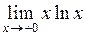 ; ;
| б) 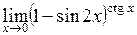 . .
|
8. Найти наибольшее и наименьшее значения функции 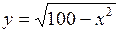 на отрезке
на отрезке 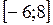 .
.
Ответы: 1. 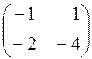 . 2. (–2; –3; –2). 3. да. 4.
. 2. (–2; –3; –2). 3. да. 4. 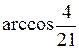 . 5. а) 3/2; б) –1/16; в) 1/18; г)
. 5. а) 3/2; б) –1/16; в) 1/18; г) 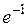 . 7. а) 0; б)
. 7. а) 0; б) 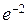 . 8.
. 8. 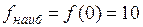 ,
, 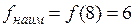 .
.
Вариант 10
1. Найти обратную матрицу 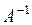 , если
, если  .
.
2. Решить систему линейных уравнений методом Гаусса:
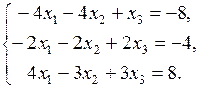
3. Вычислить объем треугольной пирамиды, вершины которой находятся в точках 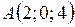 ,
, 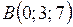 ,
, 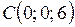 ,
, 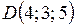 .
.
4. Определить угол между прямыми 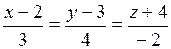 и
и 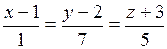 .
.
5. Вычислить пределы:
а) 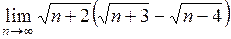 ; ;
| б) 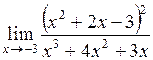 ; ;
|
в) 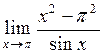 ; ;
| г) 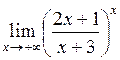 . .
|
6. Вычислить производную 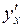 :
:
а) 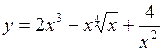 ; ;
| б) 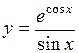 ; ;
|
в) 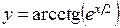 ; ;
| г) 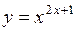 . .
|
7. Вычислить предел, применяя правило Лопиталя:
а) 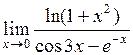 ; ;
| б) 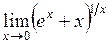 . .
|
8. Найти точки экстремума функции  .
.
Ответы: 1. 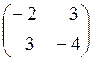 . 2. (2; 0; 0). 3. 2. 4.
. 2. (2; 0; 0). 3. 2. 4. 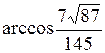 . 5. а) 7/2; б) 0; в)
. 5. а) 7/2; б) 0; в) 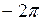 ; г)
; г) 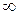 . 7. а) 0; б)
. 7. а) 0; б) 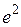 . 8.
. 8. 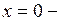 точка максимума,
точка максимума, 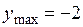 ,
, 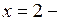 точка минимума,
точка минимума, 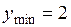 .
.
ВАРИАНТЫ ТЕОРЕТИЧЕСКИХ ТЕСТОВЫХ ЗАДАНИЙ
1. Дана матрица 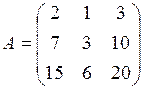 . Сумма элементов
. Сумма элементов 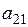 и
и 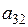 равна:
равна:
| а) 13; | б) 11; | в) 8; | г) 16; | д) 18. |
2. Даны матрицы 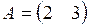 и
и 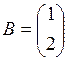 . Сумма
. Сумма 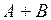 равна:
равна:
а) 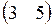 ; ;
| б) 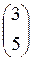 ; ;
| в) не существует; | г) (8); | д) 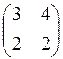 . .
|
3. Даны матрицы 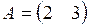 и
и 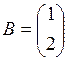 . Произведение
. Произведение 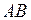 равно:
равно:
а) 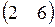 ; ;
| б) 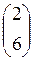 ; ;
| в) не существует; | г) (8); | д) 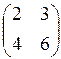 . .
|
4. Транспонированной к матрице 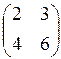 является матрица:
является матрица:
а) 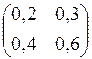 ; ;
|
б) 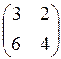 ; ;
|
в) 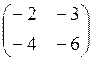 ; ;
| г) 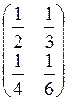 ; ;
|
д) 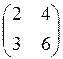 . .
|
5. Определитель 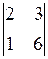 равен:
равен:
| а) –9; | б) 15; | в) 12; | г) 9; | д) 0. |
6. Если 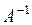 является обратной к матрице
является обратной к матрице 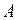 , то:
, то:
а)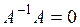 ; ;
| б)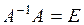 ; ;
| в) 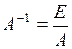 ; ;
| г)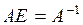 ; ;
| д)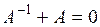 . .
|
7. Система линейных уравнений называется совместной, если:
а) она имеет единственное решение;
б) она имеет хотя бы одно решение;
в) она не имеет решений;
г) она имеет ненулевое решение;
д) она имеет бесконечно много решений.
8. Даны точки 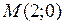 и
и 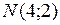 . Вектор
. Вектор 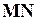 имеет координаты:
имеет координаты:
| а) (6; 2); | б) (–2; –2); | в) (2; 2); | г) (2; –2); | д) (3; 1). |
9. Модуль вектора 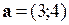 равен:
равен:
| а) 7; | б) 25; | в) 1; | г) 5; | д)3,5. |
10. Вектор 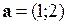 коллинеарен вектору
коллинеарен вектору 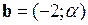 , если:
, если:
а) 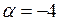 ; ;
| б)  ; ;
| в) 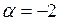 ; ;
| г) 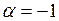 ; ;
| д) 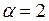 . .
|
11. Если вектор 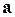 ортогонален вектору
ортогонален вектору 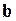 , то:
, то:
а) 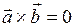 ; ;
| б) 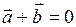 ; ;
| в) 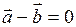 ; ;
| г) 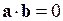 ; ;
| д) 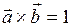 . .
|
12. Среди приведенных ниже уравнений выбрать уравнения плоскости:
а) 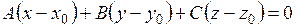 ;
;
б) 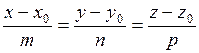 ;
;
в) 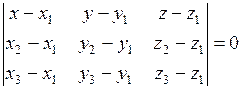 ;
;
г) 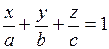 ;
;
д) 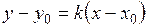 .
.
13. Направляющим вектором прямой 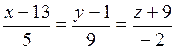 является вектор с координатами:
является вектор с координатами:
| а) (13; 1; 9); | б) (–8; 8; 7); | в)(–13;–1;9); | г) (5; –1;–2); | д) (5; 9;–2). |
14. Прямая, проходящая через точки А (–1; 2) и В (3; 4), имеет уравнение:
а) 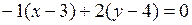 ;
;
б) 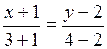 ;
;
в) 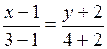 ;
;
г) 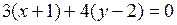 ;
;
д) 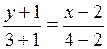 .
.
15. Прямая 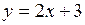 параллельна прямой
параллельна прямой 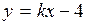 , если:
, если:
а) 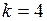 ; ;
| б) 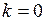 ; ;
| в) 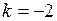 ; ;
| г) 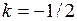 ; ;
| д) 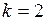 . .
|
16. Прямая 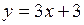 перпендикулярна прямой
перпендикулярна прямой 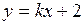 , если:
, если:
а) 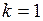 ; ;
| б) 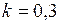 ; ;
| в) 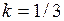 ; ;
| г) 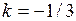 ; ;
| д) 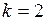 . .
|
17. Первый замечательный предел имеет вид:
а) 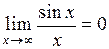 ; ;
| г) 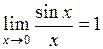 ; ;
|
б) 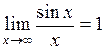 ; ;
| д) 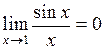 . .
|
в) 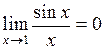 ; ;
|
18. Второй замечательный предел имеет вид:
а) 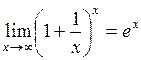 ; ;
| г) 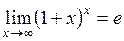 ; ;
|
б) 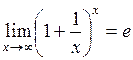 ; ;
| д) 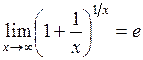 . .
|
в) 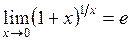 ; ;
|
19. Отметить верные утверждения:
а)  ; ;
| г) 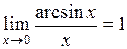 ; ;
|
б) 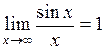 ; ;
| д) 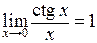 . .
|
в) 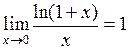 ; ;
|
20. Бесконечно малые при 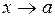 функции
функции 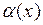 и
и  называются эквивалентными, если:
называются эквивалентными, если:
а) 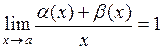 ; ;
| г) 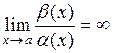 ; ;
|
б) 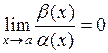 ; ;
| д) 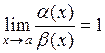 . .
|
в) 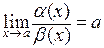 ; ;
|
21. Отметить утверждения, верные при 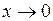 :
:
а) 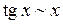 ; ;
| г) 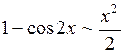 ; ;
|
б) 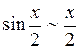 ; ;
| д) 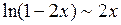 . .
|
в) 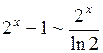 ; ;
|
22. Производная произведения 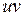 вычисляется по формуле:
вычисляется по формуле:
а) 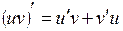 ; ;
| г) 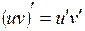 ; ;
|
б) 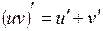 ; ;
| д) 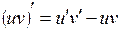 . .
|
в) 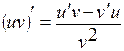 ; ;
|
23. Производная частного 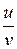 вычисляется по формуле:
вычисляется по формуле:
а) 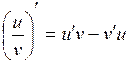 ; ;
| г) 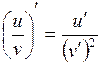 ; ;
|
б) 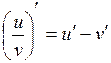 ; ;
| д) 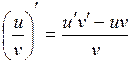 . .
|
в) 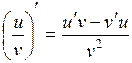 ; ;
|
24. Если функция 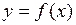 не убывает на интервале
не убывает на интервале 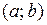 , то на этом интервале:
, то на этом интервале:
а) 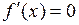 ; ;
| б) 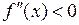 ; ;
| в) 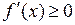 ; ;
| г) 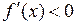 ; ;
| д) 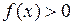 . .
|
25. Если при переходечерез точку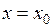 производная
производная 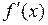 меняет знак с минуса на плюс, то
меняет знак с минуса на плюс, то 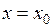 является:
является:
а) точкой перегиба;
б) точкой минимума;
в) точкой максимума;
г) точкой разрыва;
д) точкой экстремума.
Ответы:1. а). 2. в). 3. г). 4. д). 5. г). 6. б). 7. б). 8. в). 9. г). 10. а). 11. г). 12. а), в), г). 13. д). 14. а),б). 15. д). 16. г). 17. г). 18. б), в). 19. а), в), г). 20. д). 21. а), б). 22. а). 23. в). 24. в). 25. б).
ЛИТЕРАТУРА
1. Берман, Г.Н. Сборник задач по курсу математического анализа / Г.Н. Берман. – Москва: Наука, 1985. – 356 с.
2. Герасимович, А.И. Математический анализ: Справ. пособие. В 2-х ч.: ч.1 / А.И. Герасимович, Н.А. Рысюк. – Мн.: Выш. шк., 1989. – 287 с.
3. Гурский, Е.И. Руководство к решению задач по высшей математике: Учеб. пособие. В 2-х ч.: ч.1 / Е.И. Гурский, В.П. Домашов, В.К. Кравцов, А.П. Сильванович; Под общ. ред. Е.И. Гурского. – Мн.: Выш. шк., 1990. – 349 с.
4. Гусак, А.А. Высшая математика. В 2-х т.: т.1 Учебник для студентов вузов / А.А. Гусак. – Мн.: ТетраСистемс, 2001. – 544 с.
5. Гусак, А.А. Справочник по высшей математике / А.А. Гусак, Г.М. Гусак, Е.А. Бричикова. – Мн.: ТетраСистемс, 2002. – 640 с.
6. Кузнецов, В.А. Сборник задач по высшей математике (типовые расчеты): учеб. пособие для втузов / В.А. Кузнецов. – Москва: Высшая школа, 1983. – 175 с.
7. Письменный, Д.Т. Конспект лекций по высшей математике. В 2-х ч. / Д.Т. Письменный. – М.: Айрис-пресс, 2005. – 234 с.
8. Рябушко, А.П. Индивидуальные задания по высшей математике: Учеб. пособие. В 4-х ч. / А.П. Рябушко, В.В. Бархатов, В.В. Державец, И.Е. Юруть; Под общ. ред. А.П. Рябушко. – Мн.: Выш. шк., 2004. – 270 с.
|
|
|
|
|
Дата добавления: 2014-10-31; Просмотров: 392; Нарушение авторских прав?; Мы поможем в написании вашей работы!