Сложение и умножение вероятностей

Суммой А+В двух событий А и В называют событие, состоящее в появлении события А или события В, или обоих этих событий одновременно.

Вероятность суммы двух несовместных событий равна:

Р (А+В) = Р (А) + Р (В). (1.2)

Вероятность суммы несовместных событий А₁,..., А_n, образующих полную группу, равна 1, т.е.

Р (А₁+ А₂+...+ А_n) = Р (А₁) +... + Р (А_n) = 1. (1.3)

Для противоположных событий А и

Р (А) + Р () = 1. (1.4)

Пример.

На мосту с пролетами 15+24+21м находится единичная колесная нагрузка НК-80. Расположение ее в пределах одного из трех пролетов есть событие, несовместное с расположением в пределах других пролетов. Нахождение нагрузки в каждой точке по всей длине моста равновероятно.

Найти вероятности положения нагрузки на каждом из пролетов.

Решение.

Вероятность нахождения нагрузки НК-80:

на пролете 1 - ;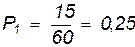

на пролете 2 - ;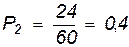

на пролете 3 - ;

Естественно, Р₁ + Р₂ + Р₃ = 1, так как здесь мы имеем полную группу событий.

Произведением АВ двух событий А и В называют событие, состоящее в совместном появлении этих событий. Для нескольких событий определение аналогично.

Условной вероятностью события В относительно события А – Р_А (В) называют вероятность события В, вычисленную в предположении, что событие А уже наступило.

Вероятность АВ произведения двух событий А и В равна произведению вероятности одного из них Р (А) на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило.

Р (АВ) = Р (А) × Р_А (В). (1.5)

Верна также симметричная формула

Р (АВ) = Р (В) × Р_В (А). (1.5')

Пример.

В железобетонной балке могут образовываться одна за другой две трещины. Вероятность появления первой по времени трещины равна: Р₁ = 0,7. Вероятность второй трещины после того, как первая уже образовалась, равна Р₁ (2) = 0,4. Требуется определить вероятности всех возможных событий: отсутствия трещин, появления одной трещины, появления двух трещин.

Решение.

Вероятность, что трещин не будет, равна

Р (0) = 1,0 – 0,7 = 0,3;

вероятность, что образуется только одна трещина, равна

Р (1) = Р₁^, Р₁ (0) = 0,7 ^, (1,0 – 0,4) = 0,42;

вероятность, что образуются обе трещины, равна

Р (2) = Р (1)^, Р₁ (2) = 0,7 × 0,4 = 0,28.

Заметим, что Р₁ (2) = 0,4 и Р₁ (0) =(1,0–0,4)= 0,6 являются условными вероятностями появления и непоявления второй трещины при условии, что первая трещина образовалась.

Событие В называют независимым от события А, если появление события А не изменяет вероятности появления события В, т.е. если Р_А (В) = Р (В). Свойство независимости событий взаимно, т.е. если Р_А (В) = Р (В), то и Р_В (А) = Р (А). Таким образом, для независимых событий:

Р(АВ) = Р(А) × Р(В). (1.6)

Для n независимых событий А₁, А₂,..., А_n вероятность появления всех событий одновременно равна

Р(А₁ А₂... А_n) = Р(А₁)^.Р(А₂)^…Р(А_n). (1.6^')

Вероятность появления хотя бы одного из независимых событий А₁, А₂,..., А_n определяется формулой:

Р(А) = 1 – q₁, q₂,..., q_n (1.7)

где q_i = Р 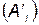= 1,0 – Р (А_i) – вероятность события, противоположного событию А_i.

Если Р (А_i) = р = const, то и q₁ = q = const и

Р (А) = 1 – qⁿ. (1.7`)

Пример.

Ребристое пролетное строение, состоящее из 5 балок, может разрушаться только в случае, если выйдут из строя все балки.

Надежность каждой балки Р_б = 0,99, вероятность ее разрушения q = 0,01.

Найти вероятность неразрушения пролетного строения.

Решение. Р = 1 – 0,01⁵.

Дата добавления: 2014-10-31