Вероятность события при многократных испытаниях

Уточнение вероятностей гипотез. Формула Бейеса

Пусть В₁,..., В_n – несовместные события (гипотезы), образующие полную группу, т.е. å Р (В_i) _i=1,...,n = 1. Произведен опыт, в результате которого произошло событие A. Спрашивается, как следует изменить вероятности гипотез в связи с появлением этого события. Иначе, необходимо найти условную вероятность для каждой гипотезы В_i в предположении, что событие А произошло, т е. Р_А (В_i). Эти вероятности определяются так называемой формулой Бейеса:

Р_А (В_i) = Р (В_i) × 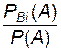(1.10)

Пример.

На строительство тоннеля пришли тюбинги с двух заводов. Известно, что тюбинги завода №1 имеют надежность 95% (т.е. брак – 5%), а завод №2 – 97%. Завод №1 поставил 60% тюбингов, а завод №2 – 40%, т.е. первоначальная вероятность, что наудачу выбранный тюбинг окажется изготовленным на заводе №1, равна 0,6, а на заводе №2 – 0,4. Наудачу выбранный тюбинг оказался качественным. Покажем, как изменятся наши представления о вероятности принадлежности этого качественного тюбинга тому или иному заводу. Вероятность, что тюбинг будет принадлежать заводу №1, по формуле Бейеса равна:

Р _№1 = 0,6 × 0,95 / (0,6 × 0,95 + 0,4 × 0,97) = 0,57 / (0,57 + 0,39) = 0,57 / 0,96 = 0,59; соответственно Р _№2 = 0,41.

Если производится несколько испытаний и в каждом из них вероятность события А не зависит от исходов других испытаний, то такие испытания называют независимыми относительно события А (выборка с возвратом).

Сложное событие – определенная комбинация нескольких простых событий (исходов испытаний).

Если вероятность события А в каждом испытании постоянна и отлична от 0 и 1, то вероятность сложного события, состоящего в том, что в «n» однородных испытаниях событие А наступит «K» раз, равна (формула Бернулли):

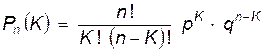, (1.11)

где p – вероятность события А в одном испытании;

q =(1 – p) – вероятность непоявления события А в испытании.

Пример.

Вероятность проектного натяжения высокопрочных болтов равна p =0.95. Найти вероятность того, что из пяти проверенных болтов два окажутся недотянуты.

Подставляем в формулу (11) значения n =5; K =2; p =0,95; q =0,05:

.

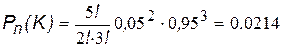При достаточно больших значениях n и K пользоваться формулой Бернулли крайне неудобно. В этих случаях вероятность Р_n (К) можно оценить приближенно по формуле Лапласа:

(1.12)

где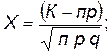

(табличная функция). (1.13)

Чем больше n, тем точнее формула (1.12).

Пример.

Вероятность проектного натяжения высокопрочных болтов равна 0.97. Найти вероятность того, что из 20 проверенных болтов 2 окажутся недотянуты.

Применим в данном случае формулу (1.12) Лапласа. При этом n =20; K =2; p =0,03; q =0,97. Вычисляем . Далее по таблице находим 0,074. И, наконец, по формуле (1.12) находим .

Интегральная формула:

Вероятность Р_n (К₁, К₂) того, что событие А в n испытаниях появится от К₁ до К₂ раз, приближенно равна:

, (1.13)

где , .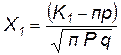

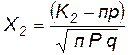Интеграл 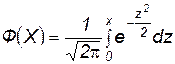- табличный (функция Лапласа).

Контрольные вопросы

1. Дайте определение понятия вероятность.

2. Дайте определение суммы и произведения двух событий.

3. Что такое условная вероятность?

4. Как определить вероятность сложного события?

Дата добавления: 2014-10-31