Определения. Основные понятия теории вероятностей

Основные понятия теории вероятностей

И математической статистики

Элементы теории вероятностей

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

Москва 2008

УДК 519.2

ББК 22.17

Настоящие методические указания являются вспомогательным, справочным материалом для студентов, обучающихся по специальности «Мосты и транспортные тоннели»при изучении ими дисциплин

«Основные понятия метрологии, стандартизации и сертификации»

и «Основы надежности транспортных сооружений».

Указания содержат основные понятия теории вероятностей и математической статистики, описание законов распределения и свойств случайных величин, приемы статистической обработки экспериментальных данных. Эти сведения необходимы для усвоения положений теории погрешностей и приложений теории надежности применительно к расчетам и оценкам технического состояния конструкций транспортных сооружений.

© Московский автомобильно-дорожный институт (государственный технический университет), 2008

Предисловие

Настоящие методические указания предназначены для студентов и магистрантов, обучающихся по специальности «Мосты и транспортные тоннели».

Учебные дисциплины «Метрология, стандартизация и сертификация» (изучается в 8-м семестре) и «Основы надежности транспортных сооружений» (9-й семестр) базируются на положениях теории вероятностей и математической статистики. Поэтому для эффективного усвоения указанных дисциплин студентам необходимо понимание основных понятий и прикладных возможностей теории вероятностей и математической статистики.

Методические указания не имеют целью повторение курса теории вероятностей в рамках изучения высшей математики на втором году обучения в институте. Они носят, в основном, справочный и прикладной характер.

Указания содержат основные термины и определения теории вероятностей, правила и процедуры операций со случайными величинами и функциями, описание наиболее распространенных законов распределения вероятностей случайных величин. Особое внимание уделяется нормальному закону распределения (распределение Гаусса), имеющему важное значение для изучения теории погрешностей в курсе метрологии и теории надежности строительных конструкций.

В разделе, посвященном математической статистике, даются способы описания экспериментальных данных теоретическими законами распределения, а также процедуры точечных и интервальных оценок случайных параметров по статистическим данным.

Все события (явления) можно разделить на следующие три вида:

Случайное – событие, которое при определенных условиях {S}, может либо произойти, либо не произойти.

Достоверное – событие, которое обязательно происходит при условиях {S}.

Невозможное – событие, которое при условиях {S} не проис­ходит.

События, которые при условиях {S} одно исключает другое, называются несовместными.

Пример

На стройплощадку привезли машину бетона, имеющего по паспорту класс В30 (объем по накладной – 3 м³):

- фактический класс бетона (по результату испытаний куби­ков) – случайное событие;

- фактический объем – случайное событие;

- наличие бетона на стройплощадке – достоверное со­бытие;

- отсутствие бетона на стройплощадке – невозможное собы­тие;

- водоцементное отношение в привезенном бетоне В/Ц=1,0, а осадка конуса – 2 см – несовместные события (при В/Ц=1 конус расплывается).

Полная группа событий – совокупность всех возможных со­бытий (исходов), которые могут произойти в результате испытаний.

Полная группа может состоять из ограниченного числа собы­тий (дискретная группа) или неограниченного (непрерывная). Непрерывную группу можно трактовать геометрически в виде линии, поверхности, объема.

Случайное, достоверное, невозможное события составляют полную группу.

Два несовместных события А и , образующих полную группу, называют противоположными.

Вероятность события А – отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных исходов, образующих полную группу.

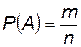, (1.1)

где Р(А) – вероятность события А;

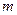– число исходов, при которых происходит событие ;

– общее число исходов.

Вероятность любого события находится в следующих пределах:

.

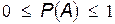Р(А) = 0 означает, что событие А – невозможно.

Р(А) = 1 означает, что событие А – достоверно.

Примеры

1) Из 8 бочонков лото с числами 1-8 выбор бочонка, содержащего цифру 9 - невозможен: Р(9) = 0.

Из 8 бочонков лото с числами 22-29 выбор бочонка, содержащего цифру 2 - неизбежен, т.е. Р(2) = 1.

В этом же случае вероятность выбора бочонка с числом, делящимся на 3 без остатка, равна:

(бочонки с числами 24, 27).

2) Среди 6 мешков с цементом, на которых указана марка цемента 400, оказалось, что два мешка содержат цемент меньшей марки. Вероятность того, что наудачу выбранный мешок содержит цемент марки 400, равна

Дата добавления: 2014-10-31