Векторно-матричное описание непрерывной системы

Обобщая записанную в примере систему уравнений состояния, запишем ее для системы порядка n.

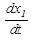= a ₁₁ x ₁ + a ₁₂ x ₂ +…+ a _{1 n} x_n + b ₁₁ u ₁ + b ₁₂ u ₂ +…+ b _{1 m} u_m,

= a ₂₁ x ₁ + a ₂₂ x ₂ +…+ a _{2 n} x_n + b ₂₁ u ₁ + b ₂₂ u ₂ +…+ b _{2 m} u_m,

…………………………………………………….

= a_{i 1} x ₁ + a_{i 2} x ₂ +…+ a_inx_n + b_{i 1} u ₁+ b_{bi 2} u ₂ +…+ b_imu_m,

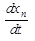= a_{n 1} x ₁ + a_{n 2} x ₂ +…+ a_nnx_n + b_{n 1} u ₁ + b_{n 2} u ₂ +…+ b_nnu_m.

Эту систему можно записать в векторно-матричной форме:

= AX + BU, (3.7)

где X = X (t) – действительный n -мерный вектор-столбец, компоненты которого переменные состояния. Поэтому он носит название вектора состояния.

U = u (t) - действительный m -мерный вектор-столбец, содержащий в качестве своих элементов входные внешние воздействия (управляющие и возмущающие), он называется вектором входа.

А – матрица коэффициентов системы размерностью (n x n), называемая матрицей системы или матрицей состояния.

B – матрица коэффициентов системы при внешних воздействиях и поэтому называемая матрицей входа; размерность матрицы B – (n x m).

Если матрицы А и В постоянные, то система называется стационарной; если матрицы А и В есть функции времени, то система называется нестационарной или системой с переменными коэффициентами.

Основное матричное уравнение (3.7.) обычно дополняется уравнением для вектора выходных переменных:

Y = CX + DU, (3.8.)

где C – матрица выхода системы, размерность которой зависит от размерности векторов X и Y; в одномерной системе, где y есть скалярная переменная, матрица С есть строка размерностью n;

D – матрица связи с внешними воздействиями, ее размерность определяется размерностью векторов U и Y.

Для матричной формы описания в пространстве состояний часто используется структурное изображение, причем в матричных структурных схемах сигналы, описываемые векторами, представляются двойными стрелками.

Так уравнению (3.7.) соответствует структурная схема (рис. 3.17, а), а схема, соответствующая уравнениям (3.7.) и (3.8.) совместно, показана на рис. 3.17, б.

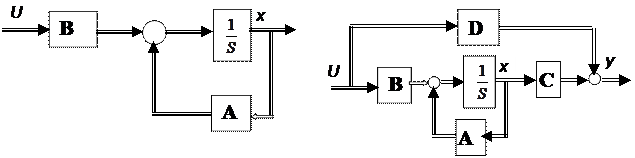а) б)

Рис. 3.17

Векторная связь через матрицу D редко встречается в обычных линейных системах с постоянными коэффициентами. Гораздо чаще используется структура с разделением управляющих и возмущающих внешних воздействий. В этом случае матрица В разделяется на две: B_u и B_f, и структурная схема приобретает вид, показанный на рис. 3.18, а.

F f

U x Y U y y

а) Рис. 3.18 б)

Для одномерной системы управления сигналы U, f и y являются скалярными величинами. Поэтому структурная схема одномерной системы будет иметь вид (рис.3.18, б). Здесь B_u и B_f вектор-столбцы, а матрица С вектор-строка.

Уравнения состояния непрерывной части системы:

, .

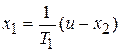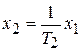Матрица системы: A = 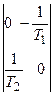. Матрица входа В = 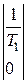, матрица выхода C = [0 1].

Определяем переходную матрицу Ф (t) = L ^-1{(SI - A)^-1}.

SI - A = s 0 – 0 - 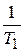= s 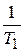; (SI-A)^T= s

0 s 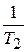0 - s s

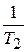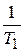(SI - A)¹==.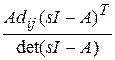

L ^-1{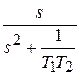} = cos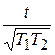; L ^-1{} = ;

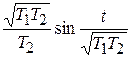L ^-1{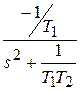}=- 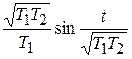. Таким образом, дискретная матрица системы:

A * = Ф (T) =

Дата добавления: 2014-10-31