Скоростные условия в очаге деформации при прокатке. 1 страница

Природа опережения.

Силы трения реактивные при осадке в гладких параллельных плитах.

W₁ = t_k1F₁

W₂ = t_k2F₂

W₁ = W₂ – сопротивления деформации

F₁ = F₂ – площади контакта

За счет скольжения скорость движения металла больше скорости плиты, которая неподвижна. В данном случае металл опережает плиту.

t_k1 ≈ t_k2 ≈ t_k – напряжения трения

Наклоним плиты.

W₁ = T_k1 – Q₁

W₂ = T_k2 – Q₂

T_k1 = t_k1F₁

T_k2 = t_k2F₂

Полагаем, что напряжения трения не изменились. Тогда, чтобы тело не было вытолкнуто из наклонных бойков, сопротивления W₁ и W₂:

t_k1 = t_k2 = t_k

W₁ = W₂

T_k1 - Q₁ = T_k2 + Q₂

T_k1 = T_k2 + (Q₁+ Q₂)

За счет изменения угла атаки в первой зоне появляется активная сила трения, которая не только уравновешивает реактивную силу T_k2, но и препятствует выталкиванию тела из наклонных плит.

Слева и справа от оси симметрии металл скользит, опережая неподвижные плиты.

t_k F₁ = t_k F₂ + (Q₁+ Q₂)

F = F₁ + F₂

t_k(F₁ - F₂) = Q₁+ Q₂

t_k(F – F₂ - F₂) = t_k(F - 2F₂) = Q₁+ Q₂

Силы трения, сформированные в зоне (F - 2F₂), представляют полярные активные силы, которые позволяют формоизменять металл, удерживая его в наклонных плитах.

Увеличивать угол α можно до тех пор, пока ось симметрии 00 не выйдет на тонкий край деформированного металла, т.е. пока F₂ не станет равной нулю.

При прокатке, отождествляя ее с осадкой в наклонных плитах, но с переменным радиусом кривизны, можно также выделить две зоны.

γ – нейтральный угол, делит очаг деформации на две зоны противонаправленными силами трения.

Таким образом, при прокатке силы трения в зоне I должны не только удержать полосу от выталкивания из валков против хода прокатки, но и сообщить полосе определенную скорость по ходу ее движения.

Суммируясь, скорости движения металла ν₀ и ν_ме дают в первой зоне результирующую скорость движения полосы, которая меньше скорости вращения валка, т.е. полоса будет отставать от валка в первой зоне. Поэтому зону I называют зоной отставания.

Во второй зоне алгебраическая сумма скоростей дает результирующую скорость движения полосы больше скорости вращения валка, т.е. полоса начинает опережать валок. Так появляется II зона опережения.

Скорость движения металла может быть равна горизонтальной составляющей скорости вращения валка только на нейтральной линии, характеризуемой углом γ.

При γ = 0 наступает буксование полосы во вращающихся валках и это предельный случай прокатки.

Активные полезные силы трения при прокатке формируются в зоне отставания, а их количество определяется величиной зоны опережения.

γ ₀ – кинематический критический угол, характеризующий протяженность зоны опережения;

γ _φ – физический критический угол, соответствующий смене знака сил трения;

γ ₁ – кинематический критический угол, характеризующий протяженность зоны отставания;

(γ ₁ - γ ₀) – углы, характеризующие протяженность зоны продольного прилипания;

3 – зона отставания;

4+5 – зона продольного прилипания;

6 – зона опережения.

От точки А до точки В растут нормальные напряжения, пропорционально которым будут увеличиваться касательные напряжения. Поскольку на этом участке силы трения направлены по ходу прокатки, то контактные слои полосы будут иметь скорость несколько большую, чем глубинные по высоте слои полосы. Но в целом средняя скорость движения полосы на этом участке будет меньше горизонтальной составляющей скорости вращения валка.

На протяжении участка ВС силы трения достигают максимально возможного значения, равного предела текучести металла на сдвиг и остаются постоянными. Тогда скольжение металла на контакте уменьшается и более интенсивно начинают деформироваться внутренние, глубинные слои полосы.

На протяжении участка СЕ относительные проскальзывания полосы и валков становятся очень малыми и силы трения в точке D меняют свое направление на противоположное.

В сечении DD, соответствующем физическому углу, скорости ν_х равномерно распределяются по высоте сечения полосы.

На протяжении участка DE силы трения, сменив свой знак, начинают сдерживать течение контактных слоев полосы и более интенсивно начинают деформироваться внутренние слои. В сечении ЕЕ силы трения, сменив свой знак, достигают максимально возможного значения, равного k, поэтому сдвиги на контакте металла с валком заменяются сдвигами внутри деформируемой полосы.

На протяжении участка FG нормальные напряжения начинают снижаться, в результате чего уменьшаются и контактные силы трения. Поэтому различия в скоростях ν_х по сечению полосы начинают уменьшаться, но в плоскостях выхода все равно различия в скоростях есть.

В зоне передней внеконтактной деформации скорости начинают выравниваться по сечению полосы, и в жестком конце мы имеем эпюру равномерного распределения скоростей.

Таким образом, зоны передней и задней внеконтактных деформаций выравнивают скорости по сечению в переднем и заднем жестких концах.

При неравномерном распределении скоростей по сечению полосы средняя скорость в любом сечении OD должна подчиняться закону постоянства секущего объема металла, проходящего через это сечение.

ν₀ S₀ = ν_{х ср} S_х = ν₁ S₁

ν₀ h₀ b₀ = ν_{х ср} h_x b_x = ν₁ h₁ b₁

∆h_x = h_x – h₁ = D(1 – cos α_x)

α_x – текущий угол

h_x = h₁ + D(1 – cos α_x)

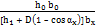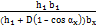ν_{х ср} = ν₀ = ν₁

ν_{х ср} – средняя скорость в любом сечении

ν_{х в} – горизонтальная составляющая скорости вращения валка

ν_{х в} = ν_в cos α_x

Это в случае, если не будет зоны продольного прилипания.

Если будет зона продольного прилипания.

При переменных значениях продольных касательных напряжений t_х, поперечные касательные напряжения t_y также будут переменными по длине и ширине очага деформации. Это связано с неравномерным уширением металла.

Результирующее напряжение при прокатке:

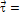
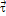_х + 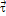_у – это величина переменная и может менять знак.

Если предположить, что t в целом средняя, то у нее будет две веточки (t_х и t_у).

Существует зона продольного прилипания, поперечного прилипания (при плоской прокатке).

При прокатке может существовать зона поперечного прилипания, в которой отсутствует проскальзывание полосы относительно валков в поперечном направлении (т.е. уширение металла близко к нулю). Сочетание зон продольного и поперечного прилипания могут дать понятие зон полного прилипания, но при прокатке маловероятно получение зоны полного прилипания. Поэтому при прокатке следует вести речь только о силах трения скольжения.

Относительное проскальзывание в плоскости, касательно к поверхности валка будет представлять собой:

νt_х – ν_b = 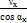- ν_b

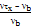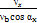Ω = = - 1

Если мы рассматриваем плоскость входа металла в валки, то угол = α₀.

Ω | α_x= α₀ = 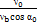- 1 – отрицательная величина.

Абсолютная величина в плоскости входа ‌: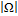

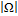‌ | α_x= α₀ = 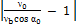= От. – отставание при прокатке.

Абсолютная величина в плоскости выхода:

Ω | α_x= 0 = 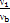- 1 = ί – величина опережения при прокатке.

Связь между опережением и отставанием:

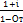= μ cos α_x

Экспериментальное определение величины опережения

Существует два метода:

1) непосредственный замер ν₁ и ν_в

2) метод керновых отпечатков

Знание скоростного режима при прокатке необходимо для безаварийной работы прокатного стана, т. к. неправильное задание скоростей вращения валков, движения металла (ν₀, ν₁), может привести к появлению продольных напряжений в металле. В результате возможен обрыв металла между клетями, его вспучивание, образование неконтролируемых петель, срыв клети с фундаментных оснований.

Кроме того, знание скоростных условий в обработке давлением позволяет правильно рассчитывать НДС, контактные напряжения (нормальные и касательные), крутящие моменты и, в целом, формоизменение металла при прокатке.

При отсутствии опережения (ί =0), металл буксует в прокатных валках. Это является предельным случаем прокатки.

При прокатке скорости ν_х, ν_y, ν_z переменны по длине, ширине и высоте в любом месте очага деформации. Для описания процессов прокатки широко используют две гипотезы.

1) гипотеза плоских сечений.

Плоское до деформации сечение остается плоским в любом месте обработки давлением.

ν_х | _z = const

ν_y | _z = var

Гипотеза плоских сечений (низкий и широкий очаг)

Эта гипотеза оправдана для низких и широких очагов деформации.

2)гипотеза прямых вертикалей.

То есть любая вертикальная линия остается вертикальной как вдоль, так и поперек очага деформации, а это возможно, если выполняется:

ν_х | _z = const

ν_y | _z = const

Гипотеза прямых вертикалей оправдана для низких и очень широких очагов деформации.

Аналитическое определение опережения при прокатке.

Используем гипотезу плоских сечений.

Закон постоянства секущего объема.

Средняя скорость ≈ ν_х.

h₀ b₀ ν₀ = h_γ b_γ ν_γ= h₁ b₁ ν₁

γ – нейтральное сечение

Но, в нейтральном сечении имеем:

ν_γ = ν_вcosγ

Обжатие и толщину полосы выразим следующим образом:

h_γ b_γ ν_b cosγ = h₁ b₁ ν₁

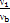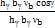ί = – 1 = -1

Будем полагать, что осуществляется плоская прокатка, тогда уширение мало и можно записать:

b_γ ≈ b₁

∆h_γ = h_γ – h₁ = D(1-cosγ)

h_γ = h₁ + D(1-cosγ)

ί = 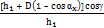- 1 – формула Финка для подсчета опережения.

Раскроем скобки в формуле Финка:

ί = (1 – cosγ) (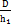 cosγ -1)

1 – cosγ = 2sin²

В связи с малыми нейтралями угла γ мы имеем:

2sin² ≈

cosγ = 1 -

ί = 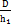- ≅ ( 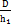-1) – формула Свена-Экелунда.

В реальных условиях прокатки тонкого листа, ленты 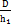на два – три порядка больше 1, поэтому единицей можно пренебречь.

Формула Головина-Дрездена:

ί =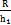

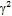
Нейтральный угол может быть определен по формуле Павлова.

γ = (1 - )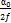

Она дает следующую графическую интерпретацию – параболу.

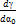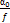= - = 0

При α₀ = f – экстремум

γ =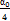

γ = 0, если α₀ = 0

α₀ = 2f

В I с увеличением α₀, γ растет.

I – область устойчивой прокатки.

II – область неустойчивой прокатки.

Формула может быть модифицирована с учетом уширения:

γ = 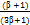(1 - ) (*)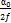

β =

Чем больше уширение, тем меньше γ меньше ί.

При прокатке на γ влияет предел текучести, натяжение, формула очага деформации.

Формулы Павлова выведены из теории равновесия сил. Более точно γ рассчитывается из кинетической теории. Это формула Выдрина:

γ = 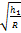tg

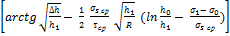
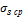– средний предел текучести

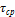– средние силы трения

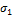и 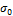– соответствующие передний и задний удельные натяжения

Рассмотрим влияние технологических факторов на ί.

ί =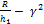

γ = (1 - )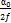

∆h = -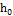

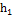
α₀ =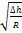

ε =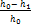

1. Диаметр валков.

С увеличением R_b при прочих равных условиях дробь 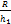возрастает, но угол α₀ начинает уменьшаться. В области устойчивой прокатки это приведет к уменьшению угла γ, в результате действия двух факторов в противоположную сторону, опережение будет изменяться по нелинейному закону.

2. Конечная толщина полосы.

С увеличением h₁, при постоянной h₀, уменьшается Δh, а следовательно и угол контакта α₀. В области устойчивой прокатки это приведет к уменьшению нейтрального угла γ. Но при возрастании h₁, дробь 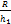будет уменьшаться, т.е. оба фактора будут действовать в одном направлении. Этим объясняется нелинейный характер зависимости.

Если прокатка осуществляется во второй области, то с увеличением h₁ дробь 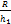по-прежнему будет убывать, а угол γ несколько возрастет. Поскольку 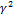, то этот фактор приведет к частичной компенсации падения опережения за счет дроби 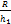. Этим объясняется стабилизация кривой.

3. Степень деформации.

В области устойчивой прокатки при h₀ = const степень деформации ε может нарастать, если будет уменьшаться толщина h₁. За счет этого дробь 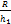будет постоянно увеличиваться. При возрастании Δh, угол контакта α₀ будет увеличиваться и в области I это приведет к увеличению угла γ, т.е. два фактора будут действовать в одном направлении и это приведет к увеличению опережения слева от точки максимума. В области II с уменьшением h₁ угол α₀, возрастая, приведет к снижению угла γ, хотя дробь 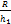по-прежнему будет возрастать, но снижение угла γ будет действовать в противоположную сторону. Этим объясняется ход кривой ί = f(ε) справа от точки максимума.

При постоянной h₁ степень деформации ε может возрастать только за счет увеличения h₀, тогда дробь 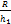остается константой, и характер изменения опережения целиком зависит от характера изменения угла γ.

При Δh = const, степень деформации ε может возрастать только за счет уменьшения исходной толщины полосы h₀. Это возможно в том случае, если будет уменьшаться и величина h₁. Тогда дробь 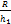будет постоянно нарастать, а угол γ будет оставаться неизменным, т.к. α₀ меняться не будет.

4. Исходная ширина полосы.

С увеличением исходной ширины будет очаг стремиться к широкому. В этом случае уширение металла будет снижаться, т.е. будет уменьшаться коэффициент поперечной деформации β. За счет этого более интенсивно будет уменьшаться знаменатель по сравнению с числителем в выражении (*), и в целом γ будет увеличиваться, и опережение будет нарастать. При достижении исходной ширины b₀ наступит плоская прокатка, когда b₀ = b₁. Этим объясняется стабилизация опережения от исходной толщины.

5. коэффициент трения.

С увеличением коэффициента трения при прокатке будет возрастать нейтральный угол γ, а, следовательно, будет увеличиваться и опережение.

6. Натяжение (переднее и заднее).

С увеличением заднего натяжения σ₀ в очаг деформации потребуется подвести больше энергии для его преодоления. Это возможно, если будет увеличиваться зона отставания и уменьшаться зона опережения, т.е. за счет уменьшения нейтрального угла γ. Таким образом, при приложении заднего натяжения, опережение будет снижаться вплоть до нуля, что будет соответствовать возможному буксованию полосы в валках.

С увеличением переднего натяжения σ₁ в очаге деформации появятся дополнительные резервные силы трения. Это приведет к возрастанию нейтрального угла, а следовательно и опережение. В пределе при достаточном уровне перед натяжением может наступить протяжка полосы через вращающиеся холостые ролики.

7. Неравномерность деформации.

Чем больше неравномерность деформации (>Е), тем меньше должен быть угол γ и раньше наступит пробуксовка, т.е. величина опережения будет уменьшаться.

В связи с неравномерностью деформации при прокатке вводят понятия: критическая линия, критическое сечение, критическая поверхность.

Критической поверхностью называют некоторую криволинейную поверхность внутри обработки деформацией, все точки которой имеют предельную скорость ν_х, равную горизонтальной проекции скорости валков на критической линии – линии пересечения критической поверхности с поверхностью валка.

В этом случае критическая поверхность будет совпадать с критическим сечением.

Если прокатка прямоугольной полосы в валках с разными скоростями (трением)

Будут появляться две критические линии. Будет два критических сечения, а поверхность одна.

Критическое сечение – это плоское сечение, через которое проходит тот же секундный объем, что и через критическую поверхность.

Формула Головина-Дрездена дает хорошие результаты в случае деформации близкой к равномерной (низкие и широкие очаги деформации).

В высоких очагах неравномерность деформации прежде всего складывается на нейтральном угле γ.

ί = 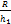(ξ γ)²

Реальный угол γ меньше γ при равномерной деформации.

Неравномерность деформации при прокатке.

Методы измерения неравномерности.

1883 – Холенберг

Метод штифтов.

Суть метода:

1) Нарушалась однородность металла

2) появлялись несплошности

1925 – Метс Н.Н.

Метод винтов

Контакт стал сплошнее. Нарушение сплошности металла.

1915 – Тринкс

Метод координатной сетки.

Недостатки только на поверхности

«Сплав Вуда» - клей, который имеет те же самые свойства, что и свинец.

Сетка наносится на любую поверхность.

Метод муарового эффекта, когда одна сетка накладывается на другую, а в отражающем свете наблюдается чередование темных и светлых полос.

Метод светочувствительных покрытий и дальнейшее развитие – голография.

Методы оценки внутри:

- скоростная пленосъемка;

- метод, связанный с появлением изоклин, изохром на металле – поляризация – оптический метод;

- рентгеновский метод;

- ультразвуковой метод.

Факторы, влияющие на неравномерность:

1) трение

В плоскости входа металла в валки в зоне отставания контактные слои будут иметь ν_х большую, чем глубинные по толщине слои. Это приведет к появлению дополнительных напряжений, неравномерно распределенных по высоте сечения.

В плоскости выхода передний жесткий конец будет стремится выровнять скорости по высоте сечения, в результате этого за плоскостью выхода металла из валков в зоне передней внеконтактной деформации уже дополнительные продольные напряжения будут неравномерно распределены по высоте полосы. В подконтактных слоях эти напряжения по-прежнему будут растягивающими, а в глубинных слоях – сжимающими.

Следовательно, различие заключается в том, что характер дополнительных напряжений в плоскости входа и задней внеконтактной зоне обусловлен в основном силами трения в очаге, а дополнительные напряжения в зоне передней внеконтактной деформации обусловлены выравнивающим действием переднего жесткого конца полосы.

Дата добавления: 2014-11-25