Теорема Вариньона о моменте равнодействующей относительно оси

Условия равновесия произвольной пространственной системы сил

Для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы сумма проекций всех сил на каждую из трех координатных осей и сумма их моментов относительно этих осей были равны нулю:

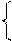åF_nx = 0; åF_ny = 0; åF_nz = 0.

åm_x(F_n) = 0; åm_y(F_n) = 0; åm_z(F_n) = 0.

Если данная система сил имеет равнодействующую, то момент этой равнодействующей относительно любой оси равен алгебраической сумме моментов слагаемых сил относительно той же оси: пусть R_x = å F_nx, тогда M_x(R) = åm_x(F_n).

Пример 2. На горизонтальный вал лежащий в подшипниках А и В насажены перпендикулярно оси вала шкив радиусом r₁ = 0.2м и барабан r₂ = 0.15м. Вал приводится во вращение ремнем, накинутым на шкив; при этом равномерно поднимается груз массой m=180кг, привязанный к веревке, которая наматывается на барабан (рис. 5.6). Пренебрегая весом вала, барабана и шкива, определить реакции подшипников А и В и натяжение Т₁ ведущей ветви ремня, если известно, что оно вдвое больше, чем Т₂ ведомой ветви. Дано: a = 0.4м; b = 0.6м; 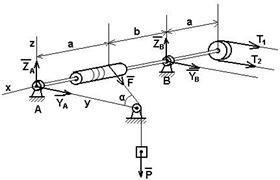a = 30⁰.

Решение: по условию задачи, груз P равномерно поднимается, это значит, что вал вращается равномерно и поэтому все силы, действующие на него, находятся в равновесии. С учетом этого составим уравнения равновесия вала. В подшипниках действуют на вал силы реакции R_Az, R_Ay, R_Bz, R_By.

Вычислим проекции всех сил на оси координат и их моменты относительно этих сил.

Fn	F = P	T1	T2	RA	RB
Fny	F cosa	T1	T2	RAy	RBy
Fnz	- F sina			RAz	RBz
mx(Fn)	-F*r2	T1*r1	– T2*r1
my(Fn)	F*b sina				- (a + b)RBz
mz(Fn)	F*b cosa	- T1*a	– T2*a		(a + b)RBy

На ось Х проекции всех сил равны нулю

P cosa + T₁ + T₂ + R_Ay + R_BY = 0 (1)

- P sina + R_Az + R_Bz = 0 (2)

r₂P + r₁T₁ – r₁T₂ = 0 (3)

b*P sina - (a + b)R_Bz = 0 (4)

b*P cosa - aT₁ – aT₂ + (a + b)R_By = 0 (5)

Решая эту систему уравнений, находим, что T₁ =2.7 kH, T₂ =1.35 kH,

R_Az = 0.36 kH, R_Ay = -6.3 kH, R_Bz, = 0.54 kH, R_By. = 0.69 kH.

Ответ: T₁ =2.7 kH, T₂ =1.35 kH, R_Az = 0.36 kH, R_Ay = -6.3 kH, R_Bz = 0.54 kH,

R_By = 0.69 kH.

Вопросы для самоконтроля

1. Как определяется момент силы относительно оси?

2. Уравнения равновесия твердого тела под действием пространственной системы сил?

3. Приведение пространственной системы сил к заданному центру?

Задачи, рекомендуемые для самостоятельного решения: 6.1 – 6.21, 7.1 – 7.12, 8.1 – 8.44 [2].

Література: [1], [3], [4].

Дата добавления: 2014-11-26