Условия равновесия произвольной плоской системы сил

Лекция 4.

Основная форма условий равновесия. Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы сумма проекций всех сил на каждую из двух координатных осей и сумма их моментов относительно любого центра, лежащего в плоскости действия сил, были равны нулю:

åF_ix = 0; åF_iy = 0; åm₀(F_i) = 0.

Вторая форма условий равновесия: Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы сумма моментов всех этих сил относительно каких-либо двух центров А и В и сумма их проекций на ось Ох не перпендикулярную к прямой АВ, были равны нулю:

åm_A(F_i) = 0; åm_B(F_i) = 0; åF_ix = 0.

Третья форма условий равновесия (уравнение трех моментов): Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы сумма всех этих сил относительно любых трех центров А, В, С, не лежащих на одной прямой, были равны нулю:

åm_A(F_i) = 0; åm_B(F_i) = 0; åm_С(F_i) = 0.

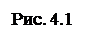
Пример 1. Определить реакции заделки консольной балки, находящейся под действием равномерно распределенной нагрузки, одной сосредоточенной силы и двух пар сил (рис. 4.1); интенсивность нагрузки q = 3*10⁴H/м; F = 4*10⁴H; m₁ = 2*10⁴H*м; m₂ = 3*10⁴H*м. BN = 3м; NC = 3м; CA = 4м.

Решение:

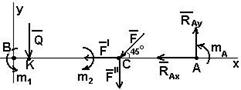
По принципу освобождаемости от связей заменим связи соответствующими реакциями. При жесткой заделке в стене возникает сила реакции R_A неизвестного направления и неизвестным моментом m_А (рис. 4.2). Распределенную нагрузку заменим эквивалентной сосредоточенной силой Q, приложенной в точке К (ВК = 1,5м). Выберем систему координат ВХУ и составим условия равновесия балки в основной форме:

проекции сил на ось Х: - Fcos45⁰ – R_Ax = 0 (1)

проекции сил на ось Y: -Q - Fsin45⁰ + R_Ax = 0 (2)

сумма моментов: m_A(F) = m₁ – m₂ + m_A + Q*KA + F”*CA = 0 (3)

Силу F разложим в точке С на две взаимно перпендикулярные составляющие F” и F’; сила F’ момента относительно точки А не создает, так как линия действия силы проходит через точку А. Модуль силы F” = Fcos45⁰ = F(2)^1/2/2.

Подставляя численные значения в уравнения (1), (2) и (3), получим:

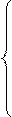
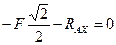
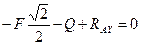
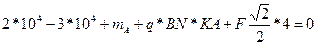
В данной системе трех уравнений имеются три неизвестные, поэтому система имеет решение и притом только единственное.

4*10⁴*0,7 = R_Ax R_Ax = 2.8*10⁴H

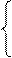
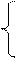
- 3*10⁴*3 – 4*10⁴*0.7 + R_Ay = 0 R_Ay = 11.8*10⁴H

m_A – 10⁴ + 3*10⁴*3*8.5 + 4*10⁴*2.8 = 0 m_A = - 86.8*10⁴H*м

Ответ: R_Ax = 2.8*10⁴H; R_Ay = 11.8*10⁴H; m_A = - 86.8*10⁴H*м.

Пример 2. Определить реакции опор А, В, С и шарнира D составной балки (рис. 4.3).

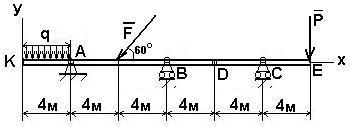q = 1,75*10⁴H/м; F = 6*10⁴H; P = 5*10⁴H.

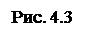Решение: По принципу освобождаемости от связей заменим связи соответствующими реакциями.

Распределенную нагрузку q заменим эквивалентной сосредоточенной силой Q = q*KA, приложенной в точке М (АМ = 2м). Количество неизвестных сил реакции: R_Ax, R_Ay, R_B, R_C и две пары составляющих сил реакции в шарнире D.

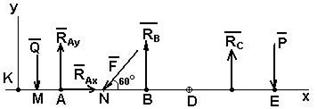
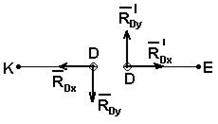Рассмотрим отдельно реакции в шарнире D. Для этого рассмотрим отдельно балки AD и DE (рис. 4.5а, 4.5б).

По третьему закону Ньютона в шарнире D на балку KD действует система сил R_Dx и R_Dy, а на балку DE система сил противоположная: R’_Dx и R’_Dy, причем модули сил попарно равны, т.е. R_Dx = R_Dx и R_Dy = R_Dy. Это внутренние силы составной балки, поэтому количество неизвестных сил реакции составляет шесть. Для их определения надо составить шесть независимых уравнений состояний равновесия. Возможны следующие варианты составления уравнений состояния.

Составляем условия равновесия для всей конструкции (3 уравнения) и для отдельного элемента этой конструкции: балки KD или балки DE. При составлении уравнений равновесия для всей конструкции внутренние силы не учитываются, так как при суммировании они взаимно уничтожаются.

Уравнения условия равновесия для всей конструкции:

R_Ax – Fcos60⁰ = 0

- Q - R_Ay – Fsin60⁰ + R_B + R_C – P = 0

m_A(F) = Q*m_A – Fsin60⁰*AN + R_B*AB + R_C*AC – P*AE = 0

Уравнения условия равновесия для элемента DE:

R’_Dx = 0

R’_Dy, + R_C – P*DE = 0

M_D(F) = R_C*DC – P*DE = 0

Таким образом составлено шесть независимых уравнений с шестью неизвестными, поэтому система уравнений имеет решение и причем только единственное. Решая систему уравнений определим неизвестные силы реакции.

Вопросы для самоконтроля

1. Три формы уравнений равновесия твердого тела?

2. Составление уравнений равновесия для составной конструкции?

Задачи, рекомендуемые для самостоятельного решения: 4.1 – 4.80 [2].

Литература: [1], [3], [4].

Дата добавления: 2014-11-26