
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Параметрическое исследование и факторный анализ систем управления
|
|
|
|
Факторные модели имеют вид (32):
Y=f(x1, x2…xn), (32)
где X-факторы или независимые переменные,
Y- функция.
Факторные модели бывают:
1. Детерминированные, когда известна связь между X и Y, при этом X принимает определённое значение.
2. Стохастическое – когда связь моделей неявна, а X принимает неопределённое значение.
Также факторные модели можно разделить на группы (по виду):
1. Аддитивные.
2. Мультипликативные.
3. Кратные.
4. Смешанные.
Задачей модели является определение степени воздействия факторов на результат. Это достигается путём:
1. Отбора факторов.
2. Классификации и систиматизации факторов.
3. Определения формы зависимостей в моделей.
4. Построения моделей в виде уравнения.
5. Оценки влияния каждого варианта в отдельности.
Факторы моделей можно классифицировать на группы:
1. Основные факторы и второстепенные факторы,
2. Внутренние и внешние.
3. Объективный и субъективный.
4. Общие и специфические.
5. Постоянные и переменные.
6. Экстенсивные (количественные) и интенсивные (качественные).
7. Простые (одноэлементные) и сложные (комплексные).
Корреляционный метод — один из экономико-математических методов исследования, позволяющий определить количественную взаимосвязь между несколькими явлениями исследуемой системы. Его называют нередко взаимосвязанным. При использовании корреляционного метода выделяют функцию, т.е. исследуемый результирующий показатель и факторные признаки, от которых зависят результирующие значения - аргументы.
Параметрические модели также, как и факторные обычно задаются в виде уравнений, имеющих вид (33):
F(x)=a2-(x2+4x)*a+x, 3(33)
Обычно ставиться вопрос, какие допустимые значения может принимать X при конкретных параметрах значение A:
- при A ≤ 0, X=0; при A 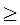 1, X=
1, X=  *(-1)+
*(-1)+ 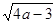 .
.
- при остальных значениях A значений X нет.
Как можно видеть от параметров зависит не только функция F, но и переменная X. В качестве параметров при исследовании систем управления используют какие-либо показатели, принимающие конкретные значения и позволяющие описать цель функционирования системы или её задачи.
Каждый такой параметр должен отвечать требованиям соответствия, критичности, устойчивости и информативности.
Соответствие параметров имеет место, если знак его измерения соответствует знаки изменения степени достижения цели системы.
Свойство критичности выполняется, если существенным изменениям параметра соответствуют существенные изменения организации.
Устойчивость показателя имеет место, если малым изменениям соответствует малое изменение функции.
Информативной считается прямо пропорциональное число параметров.
Первые три свойства являются необходимыми, последнее желательное.
Центральное место в параметрической системе управления занимает понятие «физические противоречия» Смысл применения этого метода сводится к выявлению и устранению физических противоречия, присущих исходной системе.
Физическое противоречие – взаимоисключающие требования, предъявляемые к элементу системы управления. Например: показатель, выражающий этот элемент должен иметь два различных значения.
Элемент, к которому предъявляют противоречивые требования, называют узловым элементом.
Решение параметрической задачи позволяет выявить, в каких именно областях элемент системы переменной X может принимать различные значения.
|
|
|
|
|
Дата добавления: 2014-11-26; Просмотров: 566; Нарушение авторских прав?; Мы поможем в написании вашей работы!