Случайные процессы в системах управления

Основы вариационного исчисления

Пусть имеется плоская система координат, на которой заданы следующие категории (Рисунок 3.8).

Пусть y(x) – кратчайший путь от М₁ до М₂, тогда y^x(x) – отличная от y(x) траектория на бесконечно малую величину в каждой точки пути от М₁ до М₂. Выразим это через операцию варьирования (34):

d(y)=y(x)-y^x(x), (34)

Варьирование – это бесконечно малое изменение функции при заданном значении аргумента. Именно фиксированность аргумента отличает вариацию от производной.

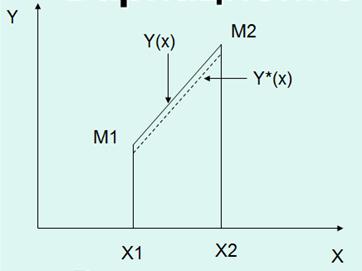
Рисунок 3.8 – Графическое изображение вариационной модели

Вариационное исчисление носило широкое применение в биологических и социологических исследованиях.

Варьирование можно определить также, как различие реакции объектов не одно и тоже входное воздействие.

В исследованиях организованных систем управления можно попытаться применить вариационное исчисление в теории мотивации, а также везде, где наблюдается влияние биологических и социальных факторов на конечный результат работы системы.

Случайными процессами называются множество случайных величин X, изменяющихся в зависимости от времени t, или другого параметра. Параметр t может быть дискретным или непрерывным.

Случайные процессы, т.к. они содержат множество случайных величин, могут быть охарактеризованы только многомерными распределениями.

Случайный процесс считается заданным, если для набора параметров <t₁, t₂…t_n> задано многомерное распределение показателей X следующего вида 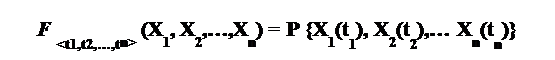(35).

(35)

Как правило, такое многомерное распределение является нормальным.

Случайные процессы X(t) называются процессами с независимыми значениями, если для любого набора от t₁…t_n случайные величины X независимы.

Независимость случайных процессов имеет многомерное распределение, которая разлагается по одномерному распределению 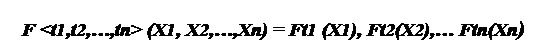(36).

(36)

Математическим ожиданием случайного процесса X(t) называется неслучайная функция. Значение средней при фиксированном значении t=t₀ равно математическому ожиданию случайной величины X(t₀).

Рассмотрим разновидность случайных процессов называемых марковскими. Случайный процесс Х (t) называется марковским, если вероятность попасть в состояние X_I=S_J в момент времени t_I зависит не от всего прошлого, а от состояния X_i-1=S₂, в котором процесс был в предыдущий момент времени. Система как бы «забывает» более длительную предисторию.

Марковские процессы, для которых разности смежных моментов наблюдения равны постоянному значению и все возможные варианты состояния перечисленных называются цепями Маркова.

Представим схему марковского процесса на рисунке 3.9.

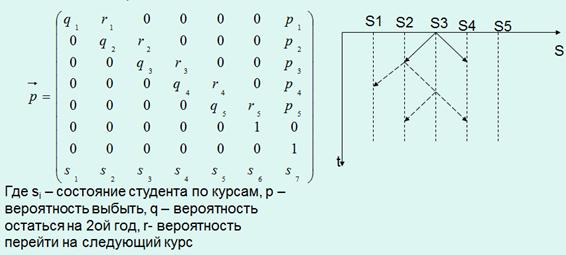
Рисунок 3.9 – Схема марковского случайного процесса

Дата добавления: 2014-11-26