
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Плоскопараллельное движение твердого тела
|
|
|
|
Математический маятник
Математический маятник – это материальная точка, подвешенная на нерастяжимой нити (рис. 11.3).
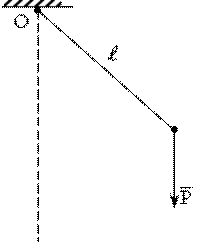
Рис. 11.3
Аналогично, как и для физического маятника, период колебания равен:
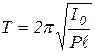 .
.
Так как 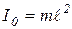 , то
, то 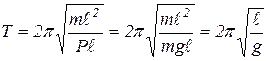 .
.
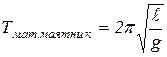 , (11.5)
, (11.5)
При условии, что 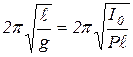 , получим:
, получим:
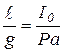 ;
; 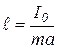 – приведенная длина физического маятника.
– приведенная длина физического маятника.
Рассмотрим плоскопараллельное движение тела (рис. 11.4).
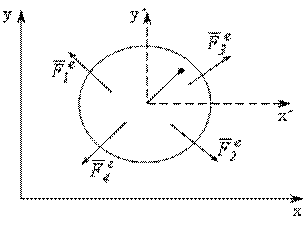
Рис. 11.4
По теореме о движении центра масс:
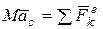 , или
, или
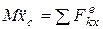 ;
; 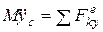 ;
; 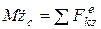 – это дифференциальные уравнения плоскопараллельного движения тела.
– это дифференциальные уравнения плоскопараллельного движения тела.
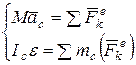 , (11.6)
, (11.6)
Задача 11.1
Барабан радиусом R, весом Р имеет выточку (как у катушки) радиусом 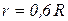 . К концам, намотанных на барабан нитей, приложены постоянные силы
. К концам, намотанных на барабан нитей, приложены постоянные силы 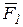 и
и 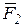 , направление которых определяется углом
, направление которых определяется углом  ; кроме сил на барабан действует пара с моментом М; когда
; кроме сил на барабан действует пара с моментом М; когда 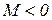 направление момента противоположна показанному на рисунке. При движении, начинающегося из состояния покоя, барабан катится без скольжения по шероховатой наклонной плоскости с углом наклона
направление момента противоположна показанному на рисунке. При движении, начинающегося из состояния покоя, барабан катится без скольжения по шероховатой наклонной плоскости с углом наклона 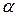 так, как показано на рис. 11.5. Пренебрегая сопротивлением качения, определить закон движения центра масс С барабана, т.е.
так, как показано на рис. 11.5. Пренебрегая сопротивлением качения, определить закон движения центра масс С барабана, т.е. 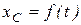 и наименьшее значение коэффициента трения
и наименьшее значение коэффициента трения 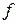 о плоскость, при котором возможно качение без скольжения. Барабан рассматривать как сплошной однородный цилиндр.
о плоскость, при котором возможно качение без скольжения. Барабан рассматривать как сплошной однородный цилиндр.
Дано: 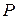 ;
; 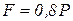 ;
; 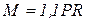 ;
; 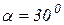 ;
; 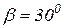 .
.
Решение
Барабан совершает плоское движение под действием сил 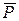 ,
, 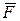 ,
, 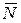 ,
, 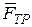 и момента
и момента 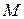 . Так как направление силы
. Так как направление силы 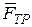 заранее неизвестно, выбираем его произвольно. Проводим оси Оху и составляем дифференциальные уравнения плоского движения.
заранее неизвестно, выбираем его произвольно. Проводим оси Оху и составляем дифференциальные уравнения плоского движения.

Рис. 11.5
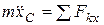 ;
; 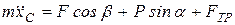 , (1)
, (1)
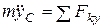 ;
; 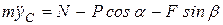 , (2)
, (2)
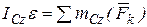 ;
; 
За положительное направление для моментов принято направление по ходу часовой стрелки.
1. Определим 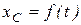 .
.
Так как 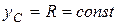 и
и 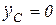 ;
;
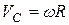 ;
;  , или
, или 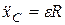 .
.
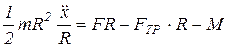 , (3)
, (3)
Делим обе части уравнения на R:
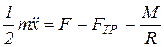 .
.
Сложим почленно (1) и (3), исключим из них 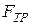 :
:
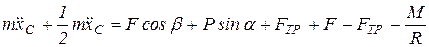 , получим
, получим
 ,
,
т.е.: 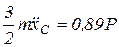 , так как
, так как 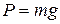 , то
, то 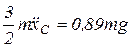 , или
, или 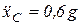 .
.
Интегрируя это дифференциальное уравнение, получим:
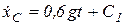 ;
; 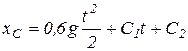 .
.
Начальные условия: 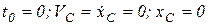 .
.
После подстановки, получим: 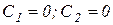 , тогда
, тогда 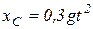 .
.
Определим 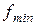 . Так как
. Так как 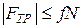 и, согласно (2)
и, согласно (2) 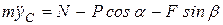 , отсюда, учитывая, что
, отсюда, учитывая, что 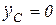 :
:
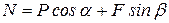 , или
, или
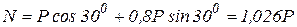 .
.
По уравнению (1), получим:
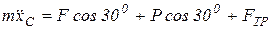 .
.
Отсюда 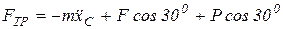 .
.
Так как 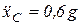 , то:
, то:
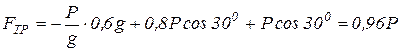 .
.
Тогда 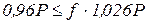 , отсюда
, отсюда 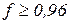 , следовательно
, следовательно 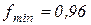 .
.
Ответ: уравнение движения центра масс барабана 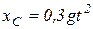 ;
;
наименьший коэффициент трения 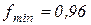 .
.
Вопросы для самоконтроля:
1. Что такое физический маятник и уравнение его движения?
2. Что такое математический маятник и уравнение его движения?
Задачи, рекомендуемые для самостоятельного решения: 39.1 – 39.23 [3].
Литература: [1] – [5].
|
|
|
|
|
Дата добавления: 2014-11-26; Просмотров: 780; Нарушение авторских прав?; Мы поможем в написании вашей работы!