Формулы для вычисления мощности

Мощностью называется величина, определяющая работу, совершаемую силой в единицу времени:

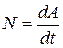, (10.22)

Единица измерения мощности – Ватт, обозначается [Вт].

Если работа совершается равномерно, то мощность определяется по формуле:

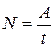, (10.23)

где А – совершенная работа;

t – время, за которое совершена данная работа.

При действии сил на вращающееся тело, мощность определяется по формуле:

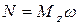, (10.24)

где – момент сил, действующих на вращающееся тело;

ω – угловая скорость тела.

При поступательном движении в случае постоянной силы, мощность определяется по формуле:

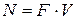, (10.25)

где F – сила, действующая на тело;

V – скорость тела.

Вычисление суммы работ сил надо выполнять в следующей последовательности:

1. изобразить на рисунке силы, приложенные к материальной точке, либо к системе материальных точек;

2. изобразить элементарные перемещения точек системы;

3. вычислить элементарную работу сил, т.е. сумму работ всех сил на элементарных перемещениях точек системы;

4. вычислить искомую сумму работ сил на конечных перемещениях как сумму определенных интегралов, взятых в соответствующих пределах от элементарных работ, вычисленных в предыдущем пункте.

При наличии сил тяжести и сил упругости можно, минуя три последних пункта, выбрав систему координат, вычислить работу этих сил на конечных перемещениях по вышеприведенным формулам.

Решение задач с помощью теоремы об изменении кинетической энергии в интегральной форме рекомендуется проводить в такой последовательности:

1. изобразить на рисунке все внешние и внутренние силы (в случае неизменяемой материальной системы – только внешние силы);

2. вычислить сумму работ всех внутренних и внешних сил на перемещениях точек системы (в случае неизменяемой материальной системы – только сумму работ внешних сил);

3. вычислить кинетическую энергию системы материальных точек в начальном и конечном положениях системы;

4. воспользовавшись результатами вычислений пунктов 2. и 3., записать теорему об изменении кинетической энергии системы материальных точек по формуле (10.16), или в случае неизменяемой системы – по формуле (10.17) и определить искомую величину.

Задача 10.2 (38.20)

Транспортер приводится в движение из состояния покоя приводом, присоединенным к нижнему шкиву В. Привод сообщает этому шкиву постоянный вращающий момент М.

Определить скорость ленты транспортера V в зависимости от ее перемещения S, если вес поднимаемого груза А равен Р ₁, а шкивы В и С радиуса r и весом Q каждый представляют собой однородные круглые цилиндры.

Лента транспортера, массой которой следует пренебречь, образует с горизонтом угол α. Скольжение ленты по шкивам отсутствует.

Рис.10.5а

Решение

Обозначим силы, действующие на объекты системы, состоящей из двух шкивов и груза.

A

h

„I”

„0”

A

S

r

C

B

M

α

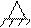
Рис.10.5 б

В системе действуют силы: 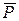– сила тяжести груза А, 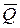- силы тяжести шкивов В и С.

Для определения скорости движения груза А по транспортерной ленте воспользуемся теоремой об изменении кинетической энергии системы:

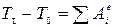, (10.24)

где: Т₀ – кинетическая энергия системы в начальном положении, так как система приводится в движение из состояния покоя, то Т₀ =0;

Т_I – кинетическая энергия системы в некотором промежуточном положении;

- сумма работ внешних сил.

Тогда:

, (10.25)

Кинетическая энергия системы равна сумме кинетических энергий каждого элемента системы:

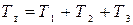, (10.26)

где: Т₁,Т₂ – кинетические энергии шкивов В и С;

Т₃ – кинетическая энергия груза А.

Так как шкивы В и С одинаковые, то Т₁=Т₂. По условию задачи, шкивы представляют однородные круглые цилиндры, тогда:

, (10.27)

где: I₀ – момент инерции шкива относительно оси вращения, ;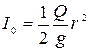

ω – угловая скорость вращения шкива.

Скорость перемещения груза А равна скорости точек на ободе шкива, поэтому: 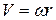, где V – скорость перемещения груза А. Тогда:

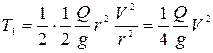, (10.28)

Рассмотрим кинетическую энергию движущегося груза А. Груз А движется по транспортерной ленте поступательно, поэтому

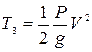, (10.29)

Подставляя формулы (10.28) и (10.29) в выражение (10.26) получим:

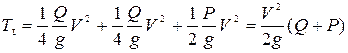, (10.30)

Рассмотрим сумму работ внешних сил:

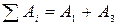, (10.31)

где: А₁ - работа, совершаемая вращающим моментом М, . φ – угол поворота шкива В;

А₃ – работа сил тяжести при перемещении груза, 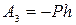. h – изменение высоты при перемещении груза из начального положения в конечное.

Перемещение груза по транспортеру из начального положения в конечное S связано с высотой подъема груза формулой:

Перемещение S связано с углом поворота шкива формулой 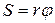, отсюда . Тогда , . Подставляя эти выражения в формулу (10.31) получим:

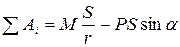, (10.32)

Подставляя выражения (10.31) и (10.32) в формулу (10.27) получим:

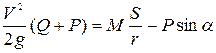
После преобразований получим:

Ответ: .

Вопросы для самоконтроля:

1. Что такое кинетическая энергия материальной точки и механической системы?

2. Теорема об изменении кинетической энергии точки и механической системы?

Задачи, рекомендуемые для самостоятельного решения: 30.1. – 30.28., 38.1 – 38.54. [3].

Литература: [1] – [5].

Дата добавления: 2014-11-26