Главный вектор и главный момент сил инерции твердого тела

Из равенств ,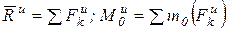

где 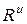– главный вектор сил инерции системы;

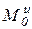– главный момент сил инерции системы относительно центра О.

Так как 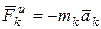и , то

.

Следовательно, главный вектор сил инерции тела, совершающего любое движение, равен произведению массы тела на ускорение его центра масс и направлен противоположно этому ускорению.

При криволинейном движении ускорение тела 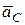разложим на касательное и нормальное, то вектор 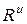разложится на составляющие:

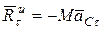, (12.6)

, (12.7)

Рассмотрим некоторые частные случаи.

1. Поступательное движение.

Так как тело не вращается вокруг центра масс С, то

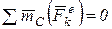, поэтому .

Отсюда следует, что при поступательном движении силы инерции твердого тела приводятся к одной равнодействующей, равной 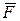и проходящей через центр масс тела.

2. Плоскопараллельное движение.

Если тело имеет плоскость симметрии и движется параллельно ей. Вследствие симметрии главный вектор и результирующая пара сил инерции, так же как и центр масс С тела, лежат в плоскости симметрии (рис. 12.1). Помещая центр приведения в точке С, получим:

, (12.8)

но так как 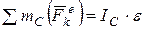, отсюда следует, что

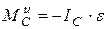, (12.9)

Таким образом, система сил инерции приводится к результирующей силе, равной 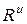и приложенной в центре масс С тела, и к лежащей в плоскости симметрии тела паре, момент которой определяется формулой:

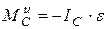
Рис. 12.1

3. Вращение вокруг оси, проходящей через центр масс тела.

Пусть тело имеет плоскость симметрии, а ось вращения CZ перпендикулярна к этой плоскости и проходит через центр масс тела. При этом 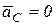, а следовательно .

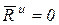Тогда система сил инерции приводится к одной паре, лежащей в плоскости, перпендикулярной к оси вращения тела, и имеющей момент.

, (12.11)

Рассмотрим решение задачи на применение принципа Даламбера.

Задача 12.1

Груз 1, силой тяжести Р₁, опускаясь вниз по наклонной плоскости, образующей с горизонтом угол 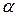приводит в движение ступенчатый каток 3, силой тяжести Р₃ посредством невесомой нерастяжимой нити переброшенной через неподвижный блок 2 силой тяжести Р₂. К блоку 2 приложен постоянный момент сопротивления . Радиусы блока 2 и катка 3 соответственно равны . Радиус инерции блока 2 относительно оси О – . Каток 3 считать однородным цилиндром. Участки нитей параллельны соответствующим плоскостям. Скольжение катка 3 по наклонной плоскости, а также нитей по блоку 2 отсутствует (рис. 12.2).

Рис. 12.2

Определить ускорение груза 1 и реакции оси блока 2, применив к решению задачи принцип Даламбера для механической системы.

Решение

Рассмотрим движение каждого тела системы отдельно.

1. Для определения ускорения груза 1 рассмотрим движение груза 1 по наклонной плоскости (рис. 12.3).

Рис. 12.3

По условию задачи груз 1 движется вниз по наклонной плоскости под действием системы сил: 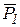– сила тяжести груза 1; 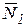– сила реакции опоры; 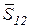– сила натяжения нити (так как рассматриваем отдельно груз 1 от системы тел, а связь заменяем силой реакции – силой натяжения 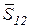). Согласно принципа Даламбера добавим к этим силам силу инерции , направленную в противоположную сторону ускорения 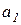. Таким образом, для груза 1 можно записать условие Даламбера:

, (1)

Проектируя это векторное уравнение на ось х, получим:

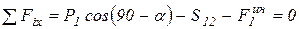, (2)

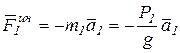где , или .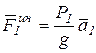

Подставляя это выражение в уравнение (2) и преобразовав, получим:

, (3)

2. Рассмотрим движение блока 2.

Блок 2 совершает вращательное движение вокруг неподвижной оси О. Выберем оси координат х и у с центром в точке О (рис. 12.4). Отбросим связи и заменим их соответствующими силами реакции. Таким образом, на тело действуют внешние силы: 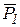– сила тяжести блока; 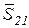– сила натяжения нити; 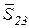– сила натяжения нити; – силы реакции оси блока О.

Рис. 12.4

Согласно принципа Даламбера необходимо к данному блоку добавить пару сил с моментом 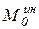будет направлен так, чтобы вращение осуществлялось против направления углового ускорения блока . Тогда, по принципу Даламбера, можно записать:

, (4,5)

Проектируя векторное уравнение (4) на оси координат, получим:

, (6)

где ;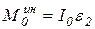

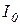– момент инерции блока относительно оси вращения О;

;

– радиус инерции блока;

– угловое ускорение блока.

Выразим угловое ускорение через ускорение первого тела .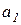

Ускорение первого тела 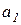будет равно касательному ускорению в точке N (рис. 12.5), т.е.:

, отсюда

.

Тогда , (7)

3. Рассмотрим плоскопараллельное движение катка 3 по наклонной плоскости.

Рассмотрим силы, действующие на каток 3: 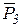– сила тяжести; 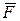– сила трения; 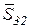– сила натяжения нити (рис. 12.5).

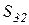
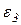
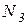
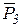
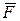
Рис. 12.5

Согласно принципа Даламбера на каток 3 действуют силы инерци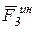и и 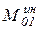– момент пары сил инерции.

Каток поднимается по наклонной плоскости вверх со скоростью центра масс 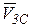. Так как точка Р является мгновенным центром скоростей, то

,

отсюда 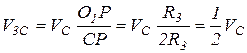, так как 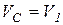, то .

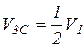Отсюда .

Так как , то .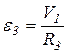

Центр масс катка движется с ускорением , поэтому сила инерции будет равна:

.

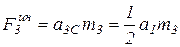Сила 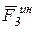направлена в сторону, противоположную направлению вектора ускорения центра масс катка .

,

где 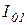– момент инерции катка относительно оси О₁.

Так как по условию задачи каток представляет однородный цилиндр, то

,

тогда .

Согласно принципа Даламбера:

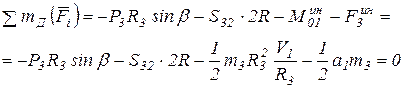, (8)

Представляя уравнения (3), (6) и (8), получим:

, (9)

В представленной системе пяти уравнений содержатся следующие неизвестные: , , 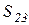, , 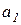(с учетом того, что 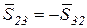). Так как число неизвестных пять, то система (9) имеет решение и притом только единственное.

Вопросы для самоконтроля:

1. Что такое принцип Даламбера?

2. Как определяется сила инерции по величине и направлению?

Задачи, рекомендуемые для самостоятельного решения: 42.1 – 42.14 [3].

Литература: [1] – [5].

Приложения

Приложение 1

Программа по теоретической механике (извлечение)

Дата добавления: 2014-11-26