Закон сохранения главного момента количеств движения

Пусть сумма моментов относительно центра О всех внешних сил, действующих на систему равна нулю:

.

Так как , то следовательно:

.

Поэтому, если сумма моментов относительно данного центра всех приложенных к системе внешних сил равна нулю, то главный момент количеств движения системы относительно этого центра будет постоянным по величине и направлению.

Пусть внешние силы, действующие на систему таковы, что сумма их моментов относительно некоторой неподвижной оси z равна нулю:

.

Тогда согласно равенству:

, следует, что:

, (9.19)

Таким образом, если сумма моментов всех действующих внешних сил на систему относительно какой-нибудь оси равна нулю, то главный момент количеств движения системы относительно этой оси будет величиной постоянной.

Внутренние силы изменить главный вектор момента количеств движения не могут.

Рассмотрим систему, вращающуюся вокруг неподвижной оси (или проходящей через центр масс системы) оси oz.

Так как ,

где – момент инерции системы относительно оси oz;

– угловая скорость системы при вращении вокруг оси oz.

Так как согласно (9.19) , то

, (9.20)

Под действием внутренних сил отдельные точки системы могут изменять свое расстояние до оси вращения. В результате этого изменяются момент инерции и угловая скорость, но так чтобы их произведение было величиной постоянной (9.20).

Задача 9.2 (37.15)

Упругую проволоку, на которой подвешен однородный шар радиусом r и массой m, закручивают на угол φ ₀, а затем предоставляют ей свободно раскручиваться. Момент, необходимый для закручивания проволоки на 1 радиан равен С.

Определить движение, пренебрегая сопротивлением воздуха, и считая момент силы упругости закрученной проволоки пропорциональным углу кручения φ.

Решение

Рис. 9.5

Применим теорему об изменении момента количеств движения для шара, подвешенного на закрученной нити. При раскручивании нити возникает момент сопротивления 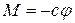, тогда:

, (1)

Для тела, вращающегося вокруг оси z с угловой скоростью, момент количества движения определяется по формуле:

, (2)

где – момент инерции шара относительно оси, проходящей через центр шара.

Для шара момент инерции равен:

, (3)

Подставляя формулу (3) в выражение (2), получим:

Подставляя это выражение в формулу (1), получим:

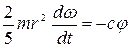, отсюда , (4)

Так как , то . Тогда, подставляя это выражение в формулу (4), получим:

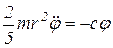, или

, (5)

Для решения полученного дифференциального уравнения второго порядка составляем соответствующее характеристическое уравнение:

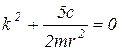
Отсюда . Так как корни характеристического уравнения мнимые, то решение уравнения (5) ищем в виде:

, (6)

где 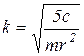. Постоянные коэффициенты С ₁ и С ₂ определяем по начальным условиям: (так как происходит свободное раскручивание). Подставляя в уравнение (6) значения начальных условий, получим:

. Отсюда .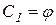

Дифференцируя уравнение (6.3.6) получим:

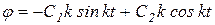. Отсюда С ₂=0, тогда уравнение (6) примет вид:

Ответ .0

Вопросы для самоконтроля:

1. Что такое момент количества движения точки и механической системы?

2. Теорема об изменении момента количества движения материальной точки и механической системы?

Задачи, рекомендуемые для самостоятельного решения: 28.4. – 28.20, 37.1 – 37.59. [3].

Литература: [1] – [5].

Дата добавления: 2014-11-26