
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теорема моментов относительно центра
|
|
|
|
Пусть материальная точка массой m движется под действием силы 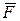 . Так как момент силы будет равен:
. Так как момент силы будет равен:
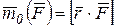 ,
,
то аналогично для вектора 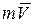 момент будет:
момент будет:
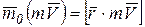 , (9.8)
, (9.8)
Дифференцируя это выражение по времени t, получим:
 .
.
Так как 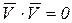 , то:
, то:
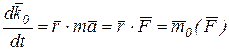 , т.е.:
, т.е.:
 , (9.9)
, (9.9)
Производная по времени от момента количества движения взятого относительно какого-нибудь центра равна моменту действующей на точку силы относительно того же центра.
Задачи с помощью теоремы об изменении момента количества движения материальной точки рекомендуется решать в следующей последовательности:
1. выбрать систему координат (при движении точки по дуге окружности следует одну из осей направить через центр окружности перпендикулярно к ее плоскости);
2. изобразить на рисунке силы, приложенные к материальной точке, т.е. активные силы и реакции связей (применив закон освобождаемости от связей);
3. вычислить суммы моментов сил, приложенных к материальной точке, относительно осей координат;
4. изобразить вектор количества движения материальной точки, записать выражение его моментов относительно неподвижных осей координат и взять от них производные по времени;
5. подставить результаты расчетов двух предыдущих пунктов решения задачи в уравнения теоремы об изменении момента количества движения материальной точки;
6. решить, в соответствии с условием, прямую либо обратную задачу динамики точки.
Задача 9.1 (28.4)
Гирька М привязана к концу нерастяжимой нити МОА, часть которой ОА пропущена через вертикальную трубку. Гирька движется вокруг оси трубки по окружности радиуса МС = R, делая 120 об/мин. Медленно втягивая нить ОА в трубку, укорачивают наружную часть нити до длины ОМ 1, при которой гирька описывает окружность радиусом 1/2 R. Сколько оборотов в минуту делает гирька по этой окружности.
Решение

Рис. 9.2
На рис. 9.2 представлено схематично условие задачи. Для решения задачи применим теорему об изменении момента количеств движения для материальной точки.
На гирю действуют силы: 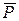 - сила тяжести,
- сила тяжести,  - сила натяжения нити. Моменты этих сил относительно оси z будут равны нулю, так как сила
- сила натяжения нити. Моменты этих сил относительно оси z будут равны нулю, так как сила 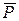 параллельна оси z, а сила
параллельна оси z, а сила  пересекает ось z.
пересекает ось z.
Тогда 
где K z – момент количеств движения гирьки относительно оси z.
Так как 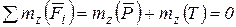 , то
, то  . Отсюда следует, что
. Отсюда следует, что  . Это означает, что при вращении гирьки вокруг оси z при изменении длины нити момент количеств движения остается постоянным.
. Это означает, что при вращении гирьки вокруг оси z при изменении длины нити момент количеств движения остается постоянным.
Для положения гирьки в точке М момент количеств движения относительно оси z будет:
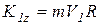 , где
, где  ,
, 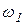 - угловая скорость вращения гирьки в положении М.
- угловая скорость вращения гирьки в положении М.
Для положения гирьки в точке 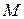 ' момент количеств движения относительно оси z будет:
' момент количеств движения относительно оси z будет:
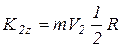 , где
, где 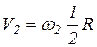 ,
, 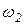 - угловая скорость вращения гирьки в положении М 1.
- угловая скорость вращения гирьки в положении М 1.
Так как момент количеств движения гирьки не изменяется, то  . Отсюда следует, что
. Отсюда следует, что  .
.
По условию задачи 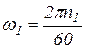 , тогда
, тогда  .
.
 , отсюда:
, отсюда:  .
.
Подставив численные значения, получим: 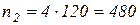 об/мин.
об/мин.
Ответ: n2 = 480 об/мин.
Задача 9.2 (28.8)
Точка М движется вокруг неподвижного центра под действием силы притяжения к этому центру. Найти скорость V 2 в наиболее удаленной от центра точке траектории, если скорость точки в наиболее близком к нему положении V 2=30 см/с, а r 2 в пять раз больше r 1.
Решение
На рис.9.3. представлена схема движения точки М массой m вокруг центра О.
Пусть в наиболее близкой от центра точке М 1 траектории скорость тела составляет V1, а в наиболее отдаленной точке М 2 траектории – V 2 (рис. 9.3).
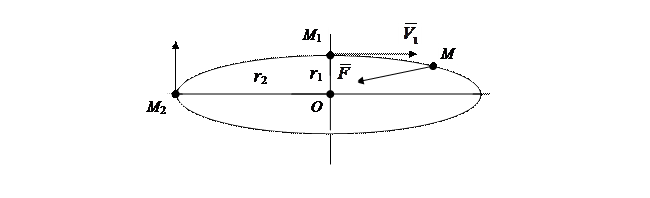
Рис. 9.3
Применим теорему моментов относительно центра:
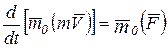 , (1)
, (1)
По условию задачи, сила, действующая на точку, является центральной, т.е. линия действия силы проходит через данную точку и центр О (рис.9.3). Поэтому момент центральной силы 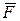 относительно центра О будет равен нулю:
относительно центра О будет равен нулю:
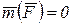 , (2)
, (2)
Из условия (2) следует, что:
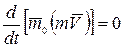 , т.е.
, т.е. 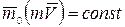 , (3)
, (3)
Обозначим момент количеств движения точки относительно центра О через  , тогда:
, тогда:
 , (4)
, (4)
Это означает, что для вектора количеств движения модуль и направление постоянные, и не меняются во времени и пространстве.
Для точки в положении М 1 модуль вектора количеств движения равен:
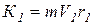 , (5)
, (5)
Соответственно для точки в положении М 2 модуль вектора количеств движения равен:
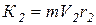 , (6)
, (6)
Так как справедливо условие (4), то выполняется равенство:
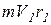 =
=  , ( 7)
, ( 7)
Отсюда следует, что:  .
.
Учитывая, что по условию задачи  , а V 1=30см/с, то V 2=
, а V 1=30см/с, то V 2=  см/с.
см/с.
Ответ: скорость точки, наиболее отдаленной от центра траектории равна V 2 = 6см/с.
|
|
|
|
|
Дата добавления: 2014-11-26; Просмотров: 981; Нарушение авторских прав?; Мы поможем в написании вашей работы!