В дифференциальной форме

Теорема об изменении количества движения точки

Материальной точки

Теорема об изменении количества движения

Лекция 8

Количеством движения называется векторная величина , равная произведению массы точки на вектор ее скорости.

Направлен вектор 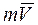так же, как и скорость точки, т.е. по касательной к ее траектории.

Вектор количества движения обозначим через 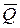, тогда:

, (8.1)

Импульс силы. Элементарным импульсом силы называется векторная величина 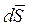, равная произведению вектора силы 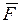на элементарный промежуток времени :

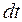, (8.2)

Направлен элементарный импульс по линии действия силы.

За конечный промежуток времени 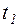импульс силы определяется по формуле:

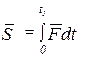, (8.3)

Проекции импульса силы на оси координат будут:

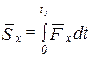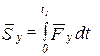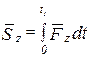, , , (8.4)

Производная по времени от количества движения точки равна геометрической сумме действующих на точку сил:

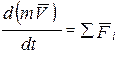, (8.5)

Теорема об изменении количества движения материальной точки в интегральной форме:

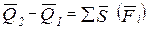, (8.6)

Изменение количества движения точки за некоторый промежуток времени равно геометрической сумме импульсов всех действующих на точку сил за тот же промежуток времени.

В координатной форме уравнение (8.6) примет вид:

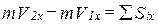
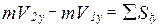(8.7)

.

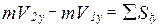Рекомендуется следующая последовательность решения задач на применение теоремы об изменении количества движения материальных точек:

1. изобразить на рисунке все силы, приложенные к материальной точке, т.е. активные силы и реакции связей (применить закон освобождаемости от связей);

2. выбрать систему координат;

3. записать теорему об изменении количества движения материальной точки (системы) в проекциях на эти оси:

;

;

.

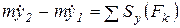Задача 8.1 (28.2)

По шероховатой наклонной плоскости, составляющей с горизонтом угол α =30˚, спускается тяжелое тело без начальной скорости. Определить, в течение какого времени Т тело пройдет путь длиной l =39,2м, если коэффициент трения f =0,2.

Решение

На рис. 8.1. схематично представлено тяжелое тело массой m, спускающееся без начальной скорости. Выбираем направление оси координат OX по ходу движения тела. Начало координат соответствует исходному положению тела на наклонной плоскости (точка О). Изобразим силы, действующие на тело в произвольном положении. На тело действуют силы: 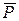-сила тяжести тела, 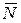- сила реакции опоры, -сила сопротивления.

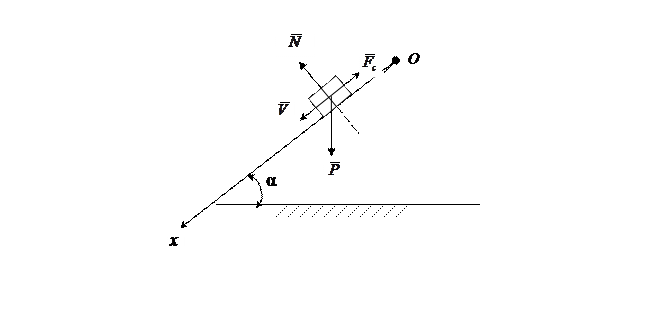
Рис. 8.1

Применим теорему об изменении количеств движения для материальной точки:

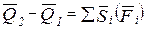, (1)

где: – вектор количества движения точки в начальный момент времени;

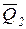– вектор количества движения точки в конечный момент времени;

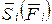– вектор сил за время движения тела.

Так как тело по условию задачи спускается без начальной скорости, т.е 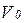= 0, , то отсюда следует, что модуль вектора количеств движения в начальный момент равен нулю 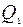= 0.

Тогда уравнение (1) будет иметь вид:

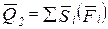, (2)

Спроектируем векторное уравнение (2) на ось x:

.

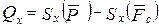Так как 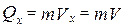, движение тела происходит по оси x.

,

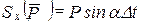
где: 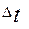– время действия сил, или время движения тела по наклонной плоскости.

Так как 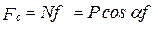, то:

, (3)

Подставляя выражение (3) в уравнение (2) получим:

, (4)

Учитывая, что Р=mg,и подставляя это выражение в уравнение (4), получим:

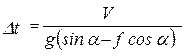, (5)

Так как на тело действуют постоянные силы, то движение будет равно-ускоренным. Тогда:

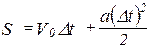, (6)

где: а – ускорение тела.

По условию задачи, начальная скорость тела равна нулю, поэтому:

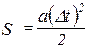, (7)

Из уравнения (7) следует:

, (8)

Скорость тела при равноускоренном движении определяется формулой:

Так как 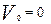, то 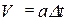. Подставляя уравнение (8) получим:

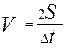, (9)

Подставляя выражение (9) в формулу (5) получим:

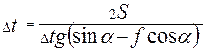
Отсюда следует, что:

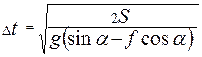
Подставляя численные значения, получим:

.

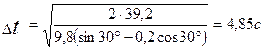Ответ: время прохождения пути составляет 4,85с.

Дата добавления: 2014-11-26