Теорема об изменении момента количеств движения системы

Главным моментом количеств движения (или кинетическим моментом) системы относительно данного центра О называется величина , равная геометрической сумме моментов количеств движения всех точек системы относительно этого центра:

, (9.10)

Моменты количеств движения системы относительно координатных осей представляются формулами:

; ; , (9.11)

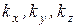представляют собой одновременно проекции вектора на координатные оси.

Главный момент количеств движения системы является характеристикой вращательного движения системы.

Рассмотрим твердое тело, вращающееся вокруг неподвижной оси z (рис. 9.4).

Рис. 9.4

Рассмотрим точку М твердого тела, находящегося на расстоянии от оси вращения z. Скорость точки М будет равной: , где – угловая скорость вращения твердого тела. Тогда для точки М массой момент количеств движения относительно оси z будет равен:

.

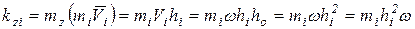Для всего тела момент количеств движения относительно оси z равен:

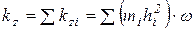, (9.12)

Учитывая, что 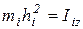– момент точки массой относительно оси z, тогда уравнение (9.12) будет иметь вид:

, т.е.:

, (9.13)

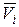Так как для одной материальной точки массой , имеющую скорость , вектор момента количеств движения будет равен:

, (9.14)

Применяя теорему об изменении момента количества движения точки, получим:

, (9.15)

Тогда для всех точек системы будет справедливо выражение:

, (9.16)

где 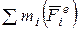– сумма моментов внешних сил, действующих на систему;

– сумма моментов внутренних сил, действующих на систему, по свойству внутренних сил:

.

Тогда уравнение (9.16) имеет вид:

, (9.17)

Полученное уравнение представляет теорему изменения моментов количества движения для системы: производная по времени от главного момента количеств движения системы относительно некоторого неподвижного центра, равна сумме моментов всех внешних сил системы относительно того же центра.

Проектируя обе части уравнения (9.17) на оси координат, получим:

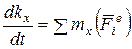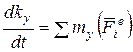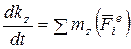; ; , (9.18)

где – момент количества движения относительно оси х;

– момент количества движения относительно оси у;

– момент количества движения относительно оси z.

Дата добавления: 2014-11-26