
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Закон сохранения движения центра масс
|
|
|
|
1. Если сумма внешних сил, действующих на систему, равна нулю, т.е. 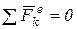 , то
, то 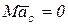 . Так как
. Так как  , то
, то 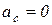 , учитывая, что
, учитывая, что 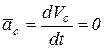 . Отсюда
. Отсюда 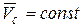 .
.
Следовательно, если сумма внешних сил, действующих на систему, равна нулю, то центр масс этой системы движется с постоянной по модулю и направлению скоростью, т.е. равномерно и прямолинейно. Если в начальный момент центр масс был в покое, то он и останется в покое. Действие внутренних сил не может изменить движения центра масс системы.
2. Пусть сумма внешних сил, действующих на систему, не равна нулю, но проекция этих сил на какую-нибудь ось, например, ось ОХ, равна нулю:
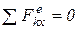 .
.
Тогда из уравнения (7.11) следует, что 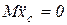 , тогда
, тогда 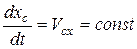 .
.
Следовательно, если сумма проекций всех действующих внешних сил на какую-нибудь ось равна нулю, то проекция скорости центра масс системы на эту ось есть величина постоянная. В частности, если в начальный момент 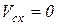 , то и в любой последующий момент
, то и в любой последующий момент 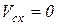 , т.е. центр масс системы вдоль оси ОХ не перемещается (
, т.е. центр масс системы вдоль оси ОХ не перемещается (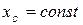 ).
).
Посредством теоремы о движении центра масс можно решать как прямые, так и обратные задачи динамики. Рекомендуется следующая последовательность решения задач:
1. изобразить на рисунке все внешние силы системы;
2. выбрать систему осей координат;
3. записать теорему о движении центра масс в проекциях на декартовы оси координат;
4. вычислить суммы проекций всех внешних сил системы на все оси декартовых координат и подставить их в уравнения (7.9).
Задача 7.1
К призме 3 массой 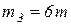 прикреплены блоки А и В радиусом
прикреплены блоки А и В радиусом  и
и 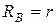 , через которые перекинуты нити, к концам которых прикреплены грузы 1 и 2 массами соответственно
, через которые перекинуты нити, к концам которых прикреплены грузы 1 и 2 массами соответственно 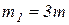 и
и 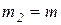 . Груз 1 спускается по закону
. Груз 1 спускается по закону 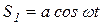 . Определить нормальное давление призмы 3 на горизонтальный пол.
. Определить нормальное давление призмы 3 на горизонтальный пол.
Решение

а) б)
Рис. 7.1
На систему, состоящую из призмы 3 и грузов 1 и 2, действуют силы: 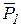 – сила тяжести груза 1;
– сила тяжести груза 1; 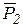 – сила тяжести груза 2;
– сила тяжести груза 2; 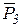 – сила тяжести груза 3;
– сила тяжести груза 3; 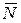 – сила реакции системы на плоскость.
– сила реакции системы на плоскость.
Выберем систему координат ХУ с началом в точке О (рис. 7.1).
Для решения задачи используем теорему о движении центра масс системы:
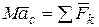 , (1)
, (1)
где 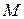 – масса системы;
– масса системы;
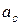 – ускорение центра масс системы.
– ускорение центра масс системы.
С учетом того, что:
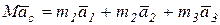 , (2)
, (2)
где 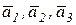 – ускорения центров масс тел системы.
– ускорения центров масс тел системы.
Проектируя векторные уравнения (1) и (2) на ось у, получим:
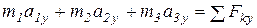 , (3)
, (3)
Пусть 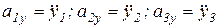 , или
, или
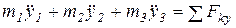 , (4)
, (4)
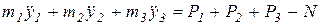 , (5)
, (5)
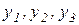 – представляют смещения центров масс тел системы при перемещении груза 1 по наклонной плоскости.
– представляют смещения центров масс тел системы при перемещении груза 1 по наклонной плоскости.
Перемещение груза 1 по наклонной плоскости из начального положения («0») в конечное («1») составляет 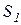 , а смещение центра масс груза по оси у составляет у1, равное:
, а смещение центра масс груза по оси у составляет у1, равное:
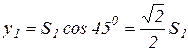 ,
,
так как 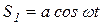 , то
, то
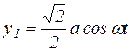 , (6)
, (6)
При перемещении груза 1 по наклонной плоскости на расстояние 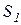 , блок, радиусом
, блок, радиусом 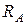 повернется на угол, равный:
повернется на угол, равный:
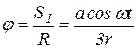 .
.
При этом перемещении груза 2 по вертикали, равное у2 определится:
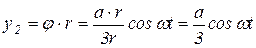 ,
,
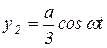 , (7)
, (7)
Тогда: 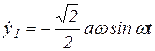 ;
; 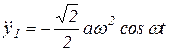 ;
;
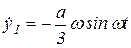 ;
; 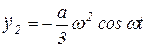 .
.
Так как движение грузов 1 и 2 не вызывает изменение центра масс призмы 3, то: 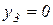 ,
, 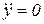 .
.
Подставляя выражения (6) и (7) в уравнение (5), получим:
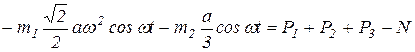 .
.
Отсюда следует, что:
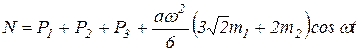 .
.
Сила нормального давления (R) призмы 3 на горизонтальный пол будет приложена к полу и направлена в противоположную сторону и по модулю равна силе нормальной реакции N, т.е.:
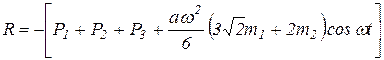 .
.
Ответ: Сила давления призмы на горизонтальный пол равна 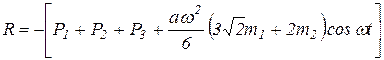 .
.
Вопросы для самоконтроля:
1. Что такое центр масс механической системы?
2. Свойства суммы внутренних сил?
Задачи, рекомендуемые для самостоятельного решения: 35.1. – 35.22. [3].
Литература: [1] – [5].
|
|
|
|
|
Дата добавления: 2014-11-26; Просмотров: 529; Нарушение авторских прав?; Мы поможем в написании вашей работы!