Тема 5.3. Методы принятия решений

Классификация и требования, предъявляемые к управленческим решениям.

Согласование решения с исполнителями и заинтересованными лицами

Выбор окончательного решения

9. Утверждение решения руководством организации или подразделения

Определение:

Управленческое решение – направленные действия для решения проблемы.

Требования:

1. Единство целей - при разработке и принятии решения должны обеспечиваться условие его непротиворечивости ранее принятым целям.

2. Научная обоснованность и правомочность - обеспечение взаимного соответствия прав и обязанностей органов принятия решения. Научная обоснованность состоит в том, чтя каждое УР должно быть обязательно аргументировано и обосновано! Аргументы должны по возможности носить формализованный характер (статистические, экономические и другие данные

3. Ясность формулировок — четкость, однозначность принятого решения и его ориентация на конкретного исполнителя.

4. Краткость формулировок принятого решения - способствует лучшему усвоению задачи исполнителем.

5. Гибкость. Решение должно предусматривать алгоритм достиже­ния цели при изменении внешних или внутренних условий, содержать описание состояний объекта управления, внешней среды, при кото­рых выполнение решения должно быть приостановлено и начата раз­работка нового решения.

6. Своевременность и оперативность принятия решений, повыша­ющие ценность принятого решения.

7. Объективность. Менеджеры не должны игнорировать фактические условия или фактическое положение дел при разработке вариантов решений. Для этого руководителю необходимо:

· получить качественную информацию, характеризующую систе­му разработки решения;

· обеспечить сопоставимость (сравнимость) вариантов решений;

· обеспечить многовариантность решений;

· достичь правовой обоснованности принимаемого решения.

8. Возможность верификации и контроля. УР должно предусматри­вать возможность его верификации и контроля. Отсутствие реальных Мероприятий по контролю, особенно когда это известно еще на ста­дии разработки решений, может делать всю остальную работу по под­готовке и принятию решений бессмысленной.

9. Автоматизация процесса сбора и обработки информации, процесса разработки и реализации решений. Решение сложных проблем должно осуществляться с использованием средств вычислительной техники, что значительно сокращает время разработки решения и повышает его обоснованность.

10. Ответственность и мотивация при принятии качественного и эффективного решения.

11. Наличие механизма реализации. Содержание решения должно включать разделы, охватывающие организацию, мотивацию и конт­роль при реализации решений.

12. У стойчивым по эффективности к воз­можным ошибкам в определении исходных данных (робастным);

13. гиб­ким — предусматривать изменение целей и алгоритмов достижения целей. В противном случае незначительные по величине отклонения исходных данных, которые могут возникнуть в любой момент и по различным причинам, будут переводить УР из разряда эффективных число неэффективных.

Классификация управленческих решений:

1. От руководящей инстанции, в которой принимается решение:

· Высшего уровня;

· Среднего уровня;

· Низшего уровня

2. Дифференциация по предмету:

· Концептуальные решения – принципиальные аспекты развития предприятия (формирование целей, планирование, организация, контроль);

· Исполнительские решения – направлены на решение отдельных позиций концептуальных решений.

3. По сфере деятельности:

· Производственные (технологические и технические);

· Сбытовые;

· Плановые;

· Кадровые и др.

4. По форме принятия:

· Единоличные;

· Коллегиальные.

1. Платежная матрица: метод статистической теории решения, помогает выбрать один из вариантов решения проблемы. Можно представить все возможные платежи в виде матрицы, в сочетании с конкретными обстоятельствами. Полезна в том случае, когда необходимо установить, какая альтернатива способна внести вклад в достижение целей.

Определение:

Платеж – денежное вознаграждение за конкретную работу (стратегию) с учетом конкретных обстоятельств.

Руководителю приходится всегда оценивать вероятность тех или иных событий. Он редко действует в условиях полной осведомленности (или неопределенности). Вероятность варьируется от 0 –событие не произойдет, до 1 –событие обязательно произойдет. Выбор значения может опираться на прежние значения или субъективную оценку руководителя. Если вероятность не принимается в расчет, то ожидания будут излишне оптимистичными.

Пример: инвестор на удачной кинокартине получает 500%дохода, а при вложении в магазин -40%. Выгоднее – кинокартина, если не принимать во внимание, что вероятность большого успеха кинокартины не велика, то вложения в магазин, покажутся более привлекательными.

Например:

1. торговый агент решает как ему выгоднее: лететь на самолете или добираться поездом до того места, где находится клиент.

Если погода хорошая, то он может полететь самолетом и потратить на дорогу 2часа, поездом же – 7 часов. Но при поездке поездом, он теряет рабочий день, который мог бы ему принести 1 500рублей. Иногородний потребитель должен вручить ему за заказ 3 000 рублей. Если погода будет плохой, из-за тумана он может позвонить клиенту, что приведет к уменьшению заказа до 500рублей, зато агент сможет получить заказы дома на 1 500рублей.

2000х0,1+4500х0,9= 4050руб; 3000х0,1+3000х0,9=3000руб Выбираем 1 вариант – наиболее доходный.

Стратегия	Вероятность той или иной погоды
Туман (0,1)	Ясная погода (0,9)
Самолет	500+1500=+2000	3000+1500=+4500
Поезд	+3000	+3000

2. Было принято решение открыть киоск с мороженым. С вероятностью 0,5 он обеспечит годовую прибыль 150 000 рублей, с вероятностью 0,2- 300 000рублей и с вероятностью 0,3 – 90 000рубей, то ожидаемое значение прибыли составит: 150х0,5+300х0,2+90х0,3=162 000рублей

Эти же деньги можно вложить в газетный киоск. С вероятностью 0,5, он будет приносить прибыль 170 000 рублей, 0,2-60 000рублей, 0,3 – 220 000рублей.

0,5х170+0,3х220+0,2х60= 171 000рублей ( выгодно); 162 000руб<171 000руб

Стратегия	Вероятность того или иного дохода
0,2	0,3	0,5
Мороженое	300 000	90 000	150 000
газеты	60 000	220 000	170 000

2. Дерево решений (коллективная экспертиза) - схематичное представление проблемы принятия решения. Как и платежная матрица дает возможность учесть различные направления действий, соотнести с ними финансовые результаты и скорректировать их с определенной вероятностью. Применение этого метода не дает готового решения, а помогает выбрать лучший результат. Полезный инструмент для принятия последовательности при решении проблемы.

Суть метода заключается в том, что группа экспертов (7-15человек) дает свою оценку всем вариантам решения проблемы, выделяя наиболее приоритетный путь (вариант) и показывая «пробелы», которым не уделили внимание.

Метод деревьев решений (decision trees) является одним из наиболее популярных методов решения задач классификации и прогнозирования.

Впервые деревья решений были предложены Ховилендом и Хантом (Hoveland, Hunt) в конце 50-х годов прошлого века. Самая ранняя и известная работа Ханта и др., в которой излагается суть деревьев решений - "Эксперименты в индукции" ("Experiments in Induction") - была опубликована в 1966 году.

В наиболее простом виде дерево решений - это способ представления правил в иерархической, последовательной структуре. Основа такой структуры - ответы "Да" или "Нет" на ряд вопросов.

На рис. приведен пример дерева решений, задача которого - ответить на вопрос: "Играть ли в гольф?" Чтобы решить задачу, т.е. принять решение, играть ли в гольф, следует отнести текущую ситуацию к одному из известных классов (в данном случае - "играть" или "не играть"). Для этого требуется ответить на ряд вопросов, которые находятся в узлах этого дерева, начиная с его корня.

Первый узел нашего дерева "Солнечно?" является узлом проверки, т.е. условием. При положительном ответе на вопрос осуществляется переход к левой части дерева, называемой левой ветвью, при отрицательном - к правой части дерева. Таким образом, внутренний узел дерева является узлом проверки определенного условия. Далее идет следующий вопрос и т.д., пока не будет достигнут конечный узел дерева, являющийся узлом решения. Для нашего дерева существует два типа конечного узла: "играть" и "не играть" в гольф.

Пример:. База данных, на основе которой должно осуществляться прогнозирование, содержит следующие ретроспективные данные о клиентах банка, являющиеся ее атрибутами: возраст, наличие недвижимости, образование, среднемесячный доход, вернул ли клиент вовремя кредит. Задача состоит в том, чтобы на основании перечисленных выше данных (кроме последнего атрибута) определить, стоит ли выдавать кредит новому клиенту.

На этапе построения модели, собственно, и строится дерево классификации или создается набор неких правил. На этапе использования модели построенное дерево, или путь от его корня к одной из вершин, являющийся набором правил для конкретного клиента, используется для ответа на поставленный вопрос "Выдавать ли кредит?"

Правилом является логическая конструкция, представленная в виде "если: то:".

На рис. приведен пример дерева классификации, с помощью которого решается задача "Выдавать ли кредит клиенту?". Она является типичной задачей классификации, и при помощи деревьев решений получают достаточно хорошие варианты ее решения.

Рис. Дерево решений "Выдавать ли кредит?"

Как мы видим, внутренние узлы дерева (возраст, наличие недвижимости, доход и образование) являются атрибутами описанной выше базы данных. Эти атрибуты называют прогнозирующими, или атрибутами расщепления (splitting attribute). Конечные узлы дерева, или листы, именуются метками класса, являющимися значениями зависимой категориальной переменной "выдавать" или "не выдавать" кредит.

Каждая ветвь дерева, идущая от внутреннего узла, отмечена предикатом расщепления. Последний может относиться лишь к одному атрибуту расщепления данного узла. Характерная особенность предикатов расщепления: каждая запись использует уникальный путь от корня дерева только к одному узлу-решению. Объединенная информация об атрибутах расщепления и предикатах расщепления в узле называется критерием расщепления (splitting criterion).

На рис. изображено одно из возможных деревьев решений для рассматриваемой базы данных. Например, критерий расщепления "Какое образование?", мог бы иметь два предиката расщепления и выглядеть иначе: образование "высшее" и "не высшее". Тогда дерево решений имело бы другой вид.

Таким образом, для данной задачи (как и для любой другой) может быть построено множество деревьев решений различного качества, с различной прогнозирующей точностью.

Качество построенного дерева решения весьма зависит от правильного выбора критерия расщепления. Над разработкой и усовершенствованием критериев работают многие исследователи.

Места, где принимаются решения, обозначают квадратами, а круг- место появления исхода.

Первая точка принятия решения	Возможные действия	События (вероятности их свершения)	Ожидаемый выигрыш	Вторая точка принятия решения	Возможные действия	Ожидаемый выигрыш
	Только электрокосилки   Только ручные косилки	Высокий спрос (0,7)   Низкий спрос на электрокосилки (0,3)   Высокий спрос на ручные косилки (0,6)     Низкий спрос на ручные косилки (0,4)	8 млн $   3 млн. $     6 млн. $   2 млн. $		Увеличение производственных мощностей для производства обоих видов косилок     Отказ от наращивания производственных мощностей	3 млн. $     1 млн. $

Пример: предположим, что руководитель предприятия по производству электро косилок решает, что расширяется рынок ручных косилок. Стоит ли выпускать электро косилки? Производство обоих типов косилок требует увеличения производственных площадей. Путем возврата от второй точки к началу наиболее предпочтительное решение – увеличение мощностей (3 млн.$).Это обусловлено ожидаемым выигрышем в 3млн. по сравнению с 1 млн. при отказе от развития производственных площадей.. Двигаемся далее назад к текущему моменту и рассчитывает решения.

Только электро косилки ожидание: 0,7*8+0,3*3=6,5

Только ручные косилки: 0,6*6+0,4*2=4,4

Следовательно, наращивание производственных мощностей для производства косилок обоих типов наиболее предпочтительное решение.

Пример 1. Главному инженеру компании надо решить, монтировать или нет новую производственную линию, использующую новейшую технологию. Если новая линия будет работать безотказно, компания получит прибыль 200 млн. рублей. Если же она откажет, компания может потерять 150 млн. рублей. По оценкам главного инженера, существует 60% шансов, что новая производственная линия откажет. Можно создать экспериментальную установку, а затем уже решать, монтировать или нет производственную линию. Эксперимент обойдется в 10 млн. рублей. Главный инженер считает, что существует 50% шансов, что экспериментальная установка будет работать. Если экспериментальная установка будет работать, то 90% шансов зато, что смонтированная производственная линия также будет работать. Если же экспериментальная установка не будет работать, то только 20% шансов за то, что производственная линия заработает. Следует ли строить экспериментальную установку? Следует ли монтировать производственную линию? Какова ожидаемая стоимостная оценка наилучшего решения?

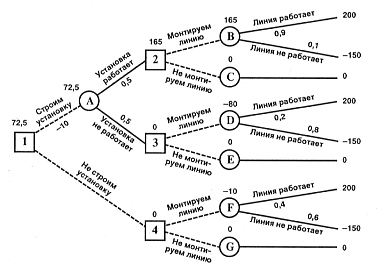
В узле F возможны исходы «линия работает» с вероятностью 0,4 (что приносит прибыль 200) и «линия не работает» с вероятностью 0,6 (что приносит убыток - 150) => оценка узла F. EMV(F) = 0,4 x 200 + 0,6 х (-150) = -10. Это число мы пишем над узлом F.

EMV(G) = 0.

В узле 4 мы выбираем между решением «монтируем линию» (оценка этого решения EMV(F) = -10) и решением «не монтируем линию» (оценка этого решения EMV(G) = 0): EMV(4) = max {EMV(F), EMV(G)} = max {-10, 0} = 0 = EMV(G). Эту оценку мы пишем над узлом 4, а решение «монтируем линию» отбрасываем и зачеркиваем.

Аналогично:

EMV(B) = 0,9 х 200 + 0,1 х (-150) = 180 - 15 = 165.

EMV(С) = 0.

EMV(2) = max {EMV(В), EMV(С} = max {165, 0} = 165 = EMV(5). Поэтому в узле 2 отбрасываем возможное решение «не монтируем линию».

EMV(D) = 0,2 х 200 + 0,8 х (-150) = 40 — 120 = -80.

EMV(E) = 0.

EMV(3) = max {EMV(D), EMV(E)} = max {-80, 0} = 0 = EMV(E). Поэтому в узле 3 отбрасываем возможное решение «монтируем линию».

ЕМV(A) = 0,5 х 165 + 0,5 х 0 — 10 = 72,5.

EMV(l) = max {EMV(A), EMV(4)} = max {72,5; 0} = 72,5 = EMV(A). Поэтому в узле 1 отбрасываем возможное решение «не строим установку».

Ожидаемая стоимостная оценка наилучшего решения равна 72,5 млн. рублей. Строим установку. Если установка работает, то монтируем линию. Если установка не работает, то линию монтировать не надо.

Пример 2. Компания рассматривает вопрос о строительстве завода. Возможны три варианта действий.

A. Построить большой завод стоимостью M1 = 700 тысяч долларов. При этом варианте возможны большой спрос (годовой доход в размере R1 = 280 тысяч долларов в течение следующих 5 лет) с вероятностью p1 = 0,8 и низкий спрос (ежегодные убытки R2 = 80 тысяч долларов) с вероятностью р2 = 0,2.

Б. Построить маленький завод стоимостью М2 = 300 тысяч долларов. При этом варианте возможны большой спрос (годовой доход в размере T1 = 180 тысяч долларов в течение следующих 5 лет) с вероятностью p1= 0,8 и низкий спрос (ежегодные убытки Т2 = 55 тысяч долларов) с вероятностью р2 = 0,2.

B. Отложить строительство завода на один год для сбора дополнительной информации, которая может быть позитивной или негативной с вероятностью p3 = 0,7 и p4= 0,3 соответственно. В случае позитивной информации можно построить заводы по указанным выше расценкам, а вероятности большого и низкого спроса меняются на p5 = 0,9 и р6 = 0,1 соответственно. Доходы на последующие четыре года остаются прежними. В случае негативной информации компания заводы строить не будет.

Все расчеты выражены в текущих ценах и не должны дисконтироваться. Нарисовав дерево решений, определим наиболее эффективную последовательность действий, основываясь на ожидаемых доходах.

Ожидаемая стоимостная оценка узла А равна ЕМV(А) = 0,8 х 1400 + 0,2 х (-400) — 700 = 340.

EMV(B) = 0,8 х 900 + 0,2 х (-275) — 300 = 365.

EMV(D) = 0,9 x 1120 + 0,1 x (-320) — 700 = 276.

EMV(E) = 0,9 x 720 + 0,1 х (-220) — 300 = 326.

EMV(2) = max {EMV(D), EMV(E)} = max {276, 326} = 326 = EMV(E). Поэтому в узле 2 отбрасываем возможное решение «большой завод».

EMV(C) = 0,7 x 326 + 0,3 x 0 = 228,2.

EMV(1) = max {ЕМV(A), EMV(B), EMV(C)} = max {340; 365; 228,2} = 365 = EMV(B). Поэтому в узле 1 выбираем решение «маленький завод». Исследование проводить не нужно. Строим маленький завод. Ожидаемая стоимостная оценка этого наилучшего решения равна 365 тысяч долларов.

Задание 1. Компания рассматривает вопрос о строительстве завода. Возможны три варианта действий.

A. Построить большой завод стоимостью M1, = 650 тысяч долларов. При этом варианте возможны большой спрос (годовой доход в размере R1 = 300 тысяч долларов в течение следующих 5 лет) с вероятностью р1 = 0,7 и низкий спрос (ежегодные убытки R2 = 85 тысяч долларов) с вероятностью p2 = 0,3.

Б. Построить маленький завод стоимостью М2 = 360 тысяч долларов. При этом варианте возможны большой спрос (годовой доход в размере T1, = 120 тысяч долларов в течение следующих 5 лет) с вероятностью р1 = 0,7 и низкий спрос (ежегодные убытки Т2 = 60 тысяч долларов) с вероятностью р2 = 0,3.

B. Отложить строительство завода на один год для сбора дополнительной информации, которая может быть позитивной или негативной с вероятностью р3 = 0,9 и р4 = 0,1 соответственно. В случае позитивной информации можно построить заводы по указанным выше расценкам, а вероятности большого и низкого спроса меняются на р5 = 0,8 и р6 = 0,2 соответственно. Доходы на последующие четыре года остаются прежними. В случае негативной информации компания заводы строить не будет.

Все расчеты выражены в текущих ценах и не должны дисконтироваться. Попробуйте самостоятельно нарисовать дерево решений и определить наиболее эффективную последовательность действий, основываясь на ожидаемых доходах. Какова ожидаемая стоимостная оценка наилучшего решения?

Нужно строить большой завод. 272,5 тысяч долларов
РАЗДЕЛ 6. КОММУНИКАЦИИ И ДЕЛОВОЕ ОБЩЕНИЕ

Дата добавления: 2014-11-09