Modus Tollens

Modus Ponens

Умова A

Імплікація A → B

Висновок B

Нехай судження А – «це літак», а судження В – «він літає». Від-повідно до правила modus ponens, якщо А правильне, то і В правильне. Іншими словами, з істинності передумови та імплікації випливає іс-тинність висновку.

Умова
B
Імплікація	A → B
Висновок
	A

У цьому випадку з істинності передумови та імплікації випливає істинність висновку. Наприклад, якщо «він не літає», то «це не літак».

Наведені вище дві (із багатьох існуючих) схеми висновку в двійковій логіці можна узагальнити на випадок нечіткості.

7.2. Правила висновку в нечіткій логіці

Припустимо, що наявні у правилах modus ponens і modus tollens судження характеризуються деякими нечіткими множинами. Далі буде записувати залежності типу «якщо А, то В» використовуючи службові слова мов програмування: if A then B.

Modus Ponens
	Умова	x is А′
	Імплікація if x is A then y is B
	Висновок	y is B′
Modus Tollens
	Умова	y is not B′
	Імплікація	if x is A then y is B,
	Висновок	x is not A′

де А, А′, В, В′ – нечіткі множини, а x і y – нечіткі лінгвістичні змінні.

7.3. Нечітка імплікація

Функції належності в логічних висновках залежать від функції

належності 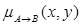нечіткої імплікації 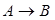, рівнозначної деякому

нечіткому відношенню 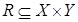. Подамо різні способи задання функ-ції 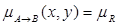на основі відомих функцій належност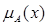і і .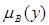

Нехай А і В – це нечіткі множини, 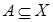, 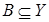. Нечіткою імплі-кацією 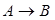називають відношення R, визначене на X × Y, що відповідає таким правилам:

1. Правило типу «мінімум» (правило Мамдані)

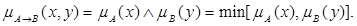
2. Правило типу «добуток» (правило Ларсена)

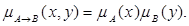
3. Правило Лукашевича

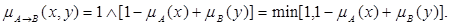
4. Правило типу «максимум-мінімум» (правило Заде)

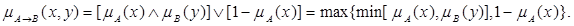
5. Бінарне правило (правило Кліна–Дейна)

µ _{A → B} (x, y) = [ 1- µ _A (x)]∨ µ _B (y) = max [ 1- µ _A (x),µ _B (y) ].

Окрім наведених є й інші означення нечіткої імплікації.

7.4. Нечіткий логічний висновок за методом Мамдані

Механізм нечіткого логічного висновку (inference) ґрунтується на

знаннях, сформованих спеціалістами цієї предметною галузі у вигляді сукупності нечітких породжувальних правил (правил логічного висновку):

if x ₁ is A ₁ and x ₂ is A ₂ and … x_n is A_n then y is B

Частину правила перед ключовим словом then («то») називають

умовою або передумовою (antecendent), а завершальну частину «y є

В» – наслідком або висновком (consequent).

Проілюструємо механізм нечіткого логічного висновку на прикладі обчислень значень функції y = f (x ₁, x ₂). Припустимо, що маємо базу знань, яка складається з двох правил:

R1: if x ₁ is A ₁₁ and x ₂ is A ₂₂ then y is B ₁ ,

R2: if x ₁ is A ₁₂ or x ₂ is A ₂₂ then y is B ₂ ,

де A_ij і B_i – це нечіткі множини, визначені для відповідних нечітких

змінних, котрі мають функції належностей µ _Aij (x) і µ _Bj (y).

Тепер за наданими значеннями x ₁ = x ₁₀ і x ₂ = x ₂₀ знайдемо конкретне y ₀ . Слід зазначити, що цей приклад легко узагальнити для довільної кілдькості вхідних (x) і вихідних (y) змінних.

Для логічного висновку приходимо за чотири кроки:

Крок 1. Введення нечіткості (fuzzification). Для чітко заданих вихідних значень розраховують ступені належності до окремих множин. Для розглядуваного прикладу визначають числові значення µ _{A 1 j} (x ₁₀) і µ _{A 2 j} (x ₂₀).

Нечітка імплікація. Знаходять функції належності перед

Крок 2. Крок 3. Крок 4.

умов кожного окремого правила за конкретних вхідних сигналів

α = µ _{A 1 j} (x ₁₀) ∩ µ _{A 2 j} (x ₂₀) – для оператора and.

j

α = µ _{A 1 j} (x ₁₀) ∪µ _{A 2 j} (x ₂₀) – для оператора or.

j

Потім знаходять вислідні функції належності кожного правила

j

µ (y) = αj∩µ _Bj (y)

Нечітка композиція (aggregation). Знаходять вислідну функцію належності всієї сукупності правил при вхідних

сигналах x ₁₀ і x ₂₀ : µ_∑(y) = µ₁(y) ∪ µ₂(y).

Зведення до чіткості (defuzzification). Використовують, коли потрібно перетворити вихідну функцію належності у

y ₀ . Крім розглянутих є багато різних методів зведення до чіткості, але найбільш поширений центроїдний метод. Якщо в наведеному алгоритмі логічна операція перетину реалізується як функція «мінімум», а об’єднання – як «максимум» (рис. 7.1), то це алгоритм Мамдані (або Мамдані–Заде).   7.5. Методи зведення до чіткості Одним з найбільш поширених методів зведення до чіткості (defuzzification) є центроїдний метод:

конкретне значення

-∞

∞ ∫

y µ_∑ (y) dy

∞

∫ -∞

y ₀ = y_c =.

(7.1)

µ_∑ (y) dy

Як бачимо формула (7.1) досить важка для обчислень, тож часто в практичних розрахунках виконують наближені обчислення, замі нюючи інтеграли відповідними сумами.

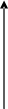
µ_A11 µ_A21 µ_B1

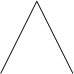
µ_A12 µ_A22 µ_B2

x ₁₀ x ₂₀

µ_Σ

Вхідні сигнали

y ₀

Рис. 7.1. Ілюстрація роботи алгоритму Мамдані

На практиці також часто використовуються такі методи:

– мінімальний максимум: результат y_cl – найменша точка, в якій

µ_∑(y) досягає максимуму;

– максимальний максимум: y_cr – найбільша точка, в якій µ_∑(y)

досягає максимуму;

m ∑ i =1

m

– середній максимум: y ₀ = y_cm = y_{i max}, де y_{i max} – точки, в яких

µ_∑(y) досягає локальних максимумів, m – кількість максимумів;

– зведення до чіткості по висоті: елементи області визначення R,

для яких значення функції належності, менші ніж певний рівень α, до

до уваги не беруть; чітке значення знаходять за такою

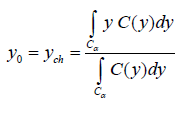
де C _α – нечітка множина α-рівня.

7.6. Нечіткий логічний висновок за методом Сугено

На практиці широко застосовують алгоритм нечіткого логічного

висновку Сугено (Sugeno), відомий також як алгоритм Такагі–Сугено–

Канга (TSK). Відмінною рисою цього алгоритму є простота обчислень.

Проджувальні правила в алгоритмі Сугено мають такий вигляд:

if x ₁ is A ₁ and x ₂ is A ₂ and … x_n is A_n then y = f_r (x ₁,..., x_n),

де f_r – звичайна чітка функція; r – номер правила.

Принципова відмінність від алгоритму Мамдані в цьому разі –

висновок, який подають у формі функціональної залежності.

Реалізація алгоритму Сугено складається із трьох кроків:

Крок 1. Введення нечіткості. Цілком аналогічне алгоритмові Мам-

дані.

Крок 2. Нечітка імплікація. Знаходяться функції належності перед-

умов кожного окремого правила за конкретних вхідних сиг-

налів x_{i 0} :

α _r , r =1, 2,..., m,

де m – кількість породжувальних правил. У класичному ал-

горитмі Сугено логічна операція перетину реалізується як

min.

Крок 3. Зведення до чіткості. Визначається чітке значення вихідної

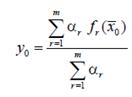змінної:

Як функцію f_r часто використовують поліноми нульового порядку:

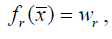
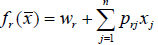
Або першого порядку:,, де w_r і p_rj – деякі сталі.

Їх називають алгоритмами Сугено нульового або першого порядку відповідно.

Зазначимо, що відомий алгоритм Ванга–Менделя відрізняється

від алгоритму Сугено нульового порядку тільки тим, що ступінь на-

лежності передумов правил у ньому знаходять за допомогою операції

множення.

Існує безліч алгоритмів нечіткого висновку, які відрізняються на-

бором вихідних правил, видом функцій належності, способами нечіт-

кої імплікації та композиції, а також методом зведення до чіткості.

8. СИНТЕЗ СИСТЕМ З НЕЧІТКОЮ ЛОГІКОЮ

Дата добавления: 2014-11-16