Несобственные интегралы первого рода

Методические указания

Тема 4.3. Несобственные интегралы

Вопросы для самопроверки

Решение.

Объем тела вращения

Объем тела, образованного вращением непрерывной кривой у = f(x), хє[a,b] вокруг оси ОХ, вычисляется по формуле

.

Пример 4.2.11. Вычислить объем тела, образованного вращением ли­нии у=chx, xє[0,l] вокруг оси ОХ.

.

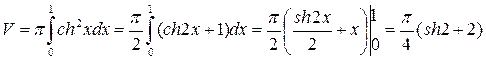1. Дайте определение определенного интеграла.

2. Приведите свойства определенного интеграла.

3. Укажите классы функций, интегрируемых по Риману.

4. Чему равна производная от определенного интеграла с переменным верх­ним пределом?

5. Приведите геометрический смысл определенного интеграла.

6. Объясните формулу площади криволинейного сектора, граница которого задана в полярной системе координат.

7. Дайте определение квадрируемой фигуры и ее площади.

8. Приведите геометрический смысл теоремы о среднем для определенного интеграла.

Учебники: [7, гл. 9, § 3], [16, гл. 14, § 4J, [33, ч. 2, гл. 4, §§ 4.13, 4.14].

Аудиторная работа: [3, №№ 2367, 2369, 2371, 2373, 2375, 2377, 2379, 2381, 2383, 2387, 2389, 2391, 2393, 2395, 2397, 2399, 2401, 2405, 2407, 2411, 2413, 2415, 2417], [7, гл. 9, №№ 75, 77, 79, 81, 83, 85, 87, 89, 91, 93, 95, 97, 99, 101, 103, 107], [20, ч. 1, №№ 6.411, 6.413, 6.415, 6.417, 6.419, 6.423, 6.425, 6.427, 6.429, 6.431, 6.433,6.435, 6.437, 6.439, 6.441, 6.443, 6.445, 6.447, 6.451], [38, №№ 9.2.1 - 9.2.12, 10.2.1 - 10.2.8].

Самостоятельная работа: [3, №№ 2368, 2370, 2372, 2374, 2376, 2378, 2380, 2382, 2384, 2386, 2388, 2390, 2392, 2394, 2396, 2398, 2400, 2404, 2406, 2410, 2412, 2414, 2416], [7, гл. 9, №№ 78, 80, 82, 84, 86, 88, 90, 92, 94, 96, 98, 100, 102, 104, 106], [20, ч. 1, №№ 6.412, 6.414, 6.416, 6.418, 6.420, 6.422, 6.426, 6.428, 6.430, 6.432, 6.434, 6.436, 6.438, 6.442, 6.444, 6.446, 6.450], [38, №№9.3.1-9.3.8, 10.3.1 - 10.3.8].

Определение. Пусть функция f(x) определена на интервале [а,∞) и для любого А>а интегрируема по Риману на сегменте [а,А]. Несобственным интервалом первого рода от функции f(x) по промежутку [а,∞) называется предел . Если этот предел существует, то интеграл называется сходящимся, в противном случае - расходящимся.

Аналогично определяются следующие интегралы:

.

Дата добавления: 2014-11-20