Указания. Тема 5.1. Уравнения первого порядка

Тема 5.1. Уравнения первого порядка

Вопросы для самопроверки

1. Дайте определение несобственного интеграла первого рода. Укажите его геометрический смысл.

2. Сформулируйте необходимый признак сходимости несобственного инте­грала первого рода. Чем он отличается от достаточных признаков сходи­мости?

3. Приведите признаки сравнения сходимости несобственных интегралов первого рода.

4. Дайте определение несобственного интеграла второго рода в случаях, ко­гда особая точка функции расположена:

а) на левом конце интервала интегрирования;

б) на правом конце интервала интегрирования;

в) внутри интервала интегрирования.

5. Сформулируйте признаки сравнения сходимости несобственных интегра­лов второго рода.

6. Приведите модельные интегралы, которые используются в признаках сравнения несобственных интегралов первого и второго рода. При каких значениях параметра а они сходятся и при каких расходятся?

Раздел 5. Дифференциальные уравнения

Учебники: [16, гл. 15, §§ 1 - 2], [22, гл. 1, §§ 1 - 7], [17, гл. 13, §§3-9, 13, 14].

Аудиторная работа: [20, гл. 9, § 1; №№ 9, 26, 28, 45, 55, 65, 77, 84, 87, 98, 129], [15, гл. 12, §§ 2, 3, 6, №№ 2062, 2067, 2084, 2095, 2097, 2104, 2156 (2)], [30, задание 1, п. 1.1: №№ 2, 6; п. 1.2: № 8; п. 1.3: № 3; п. 1.4: №№ 5, 10; п. 1.5: №2].

Самостоятельная работа: [20, гл. 9, § 1, №№ 9, 22 - 25, 43, 44, 46 - 54, 64, 66, 67 - 73, 83, 85, 86, 88, 96, 102, 122, 124], [15, гл. 12, §§ 2, 3, 6, №№ 2061, 2063 - 2066, 2093 - 2103, 2105, 2155, 2156], [30, задание 1, п. 1.1: №№ 1 - 10; п. 1.2: №№ 1 - 7; п. 1.3: №№ 1 - 5; п. 1.4: №№ 1 - 12; п. 1.5: №№ 3 - 6].

Перед изучением этого раздела рекомендуется основательно вспомнить дифференцирование и интегрирование функции одной вещественной пере­менной. Студент должен уметь:

а) находить производные от достаточно сложных элементарных функ­ций;

б) интегрировать дробно-линейные, тригонометрические, простейшие
иррациональные функции;

в) пользоваться формулами интегрирования по частям и замены переменной в неопределенном интеграле.

Дифференциальным уравнением первого порядка называется функцио­нальное уравнение F(x,y,y') = 0 или у' = f(x,у), связывающее между собой независимую переменную х, искомую функцию у = у(х) и ее производную .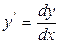

Решением данного уравнения называется любая функция у = φ(х), ко­торая, будучи подставлена в это уравнение вместе со своей производной у' = (φ(x))^’, обращает его в тождество. Например, функция 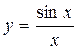есть решение дифференциального уравнения ху' + у = cosx, т. к.

.

Дифференциальное уравнение имеет бесконечное количество решений; на­пример, из простейшего уравнения у^’ = х² сразу найдем с помощью интегрирования .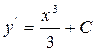

Общее решение уравнения является записью всего многообразия его решений; оно включает произвольную постоянную. Придавая ей конкретные численные значения, получаем частные решения.

Задача о нахождении частного решения уравнения при заданном на­чальном условии называется задачей Коши.

Пример 5.1.1. Найти решение уравнения у' = х², удовлетворяющее ус­ловию y(l) = 2. Из общего решения при подстановке вместо х единицы, по­лучим 1/3 + С = 2, следовательно, С = 5/3. Искомое частное решение: y=(x³+5)/3.

Уравнение считается проинтегрированным в квадратурах, если общее решение получено в явной или в неявной форме, которая может содержать еще не взятые интегралы от известных функций.

Имеется несколько классов уравнений, интегрируемых в квадратурах. Это так называемые уравнения с разделяющимися переменными, однород­ные, в полных дифференциалах, линейные относительно у и у^’, Бернулли,

Лагранжа, Клеро и некоторые другие [16, гл. 15, § 4].

Дата добавления: 2014-11-20