
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Контрольной работы № 3
|
|
|
|
Дополнение 5.1. Образец выполнения и оформления
Вопросы для самопроверки
1. Сформулируйте теорему существования и единственности решения дифференциального уравнения первого порядка.
2. Приведите примеры из классов уравнений первого порядка, интегрируемых в квадратурах.
3. Какие уравнения высших порядков допускают понижение?
4. В чем состоит метод вариации постоянных для линейного уравнения второго порядка? Приведите пример.
5. Приведите пример решения дифференциальных уравнений нахождения интегрируемых комбинаций.
6. Сформулируйте теорему существования и единственности решения системы уравнений первого порядка.
7. В каком виде ищут частные решения неоднородного уравнения, если его
правая часть имеет следующий вид: а) е2х, б) sin√3x, в) 2х-1, г) x2+cosx.
После изучения 3, 4, 5 разделов студент должен выполнить контрольную работу № 3.
"Функции нескольких переменных. Интегрирование функций одной
переменной. Обыкновенные дифференциальные уравнения"
Первые пять заданий контрольной работы № 3, которые относятся к теме "Функции нескольких переменных", подробно рассмотрены в разделе 3, примеры 3.1.1, 3.1.2, 3.2.1, 3.2.2 и 3.3.1.
Примеры решения задач к разделам 4,5
Вычислить интегралы:
1. 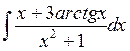
Решение. Поделим почленно числитель подынтегральной функции на знаменатель
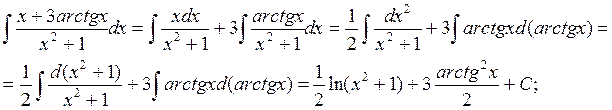
2. 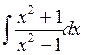
Решение. Заметим, что подынтегральная функция является неправильной дробью, т. к. степень числителя выше степени знаменателя. Поделим числитель на знаменатель. В результате получим 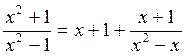 . Разложим правильную дробь
. Разложим правильную дробь 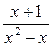 на простейшие:
на простейшие:
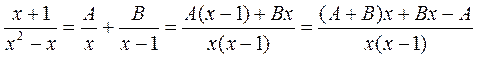
Приравнивая коэффициенты при одинаковых степенях х, получим систему 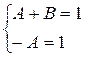 . Решение системы: А = -1;В = 2. Получим разложение
. Решение системы: А = -1;В = 2. Получим разложение 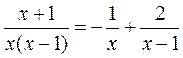 . Тогда
. Тогда
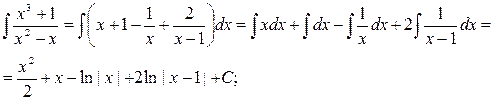
3. 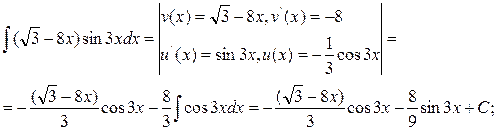
4. 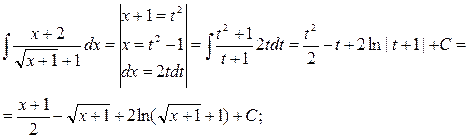
5. 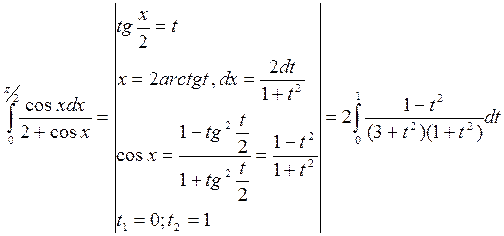 .
.
Универсальной тригонометрической подстановкой вычисление интеграла от тригонометрической функции свелось к вычислению интеграла от дробно-рациональной функции. Разложим подынтегральную дробь на простейшие дроби
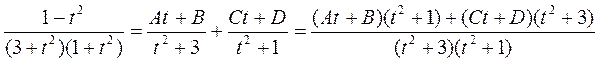 ,
,
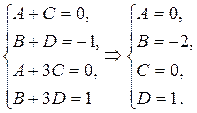
Таким образом,
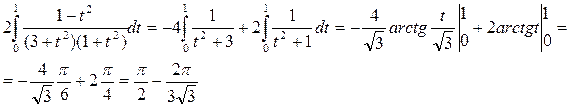 ;
;
6. Вычислить площадь фигуры, ограниченной линией 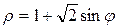 . Построим кривую
. Построим кривую 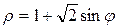 (рис.Д.5.1). Область определения
(рис.Д.5.1). Область определения 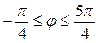 ж
ж
 |
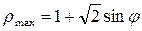 при
при 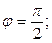
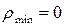 при
при 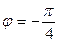 и
и 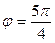 ;
;
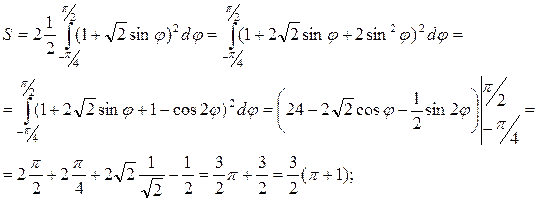
7. Исследовать сходимость
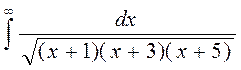 .
.
Решение. На интервале [l,∞) 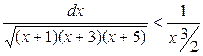 .
.
Так как  , то интеграл
, то интеграл 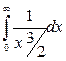 сходится, следовательно, по первому признаку сравнения сходится
сходится, следовательно, по первому признаку сравнения сходится 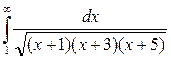 .
.
8. Решить дифференциальные уравнения первого порядка.
1) (2х3 +3xy2)dx + y3dy = 0.
Решение. Это однородное уравнение. Введем подстановку у=хu(х),
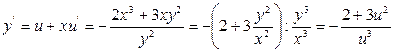 ,
,
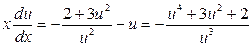 , разделим переменные
, разделим переменные
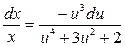 и проинтегрируем
и проинтегрируем
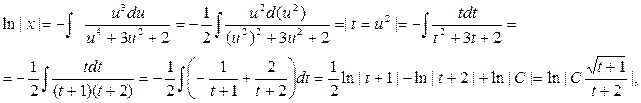
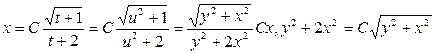 .
.
Ответ: 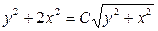 .
.
2) Найти решение уравнения у’ + ycosx = sinxcosx, удовлетворяющее условию у(0) = 1.
Решение. Это линейное уравнение первого порядка. Сначала рассмотрим соответствующее однородное уравнение у' + ycosx = 0. Разделим переменные dy/y = -cosxdx и проинтегрируем ln|y| = -sinx + lnС, у = Се-sinx. Далее методом вариации произвольной постоянной решение исходного уравнения ищем в виде y = φ(x) е-sinx: φ’е-sinx - φе-sinx cosx + φе-sinx cosx = cosxsinx, dφ/dx = sinxcosxеsinx, φ(x) = ∫sinxеsinx dsinx = ∫ueudu = ∫udeu = ueu - ∫eudu = eu(u-1) + C = esinx(sinx - 1) +C. Таким образом, общее решение имеет вид y = sinx - l + Ce-sinx. Удовлетворим условию у(0)= -1 + С = 1, С = 2.
Ответ: y = sinx - l + 2e-sinx.
9. Решить уравнения второго порядка.
1) yy” = y’2.
Решение. Уравнение не содержит явно х, поэтому его порядок понижается подстановкой у '=z(y), причем
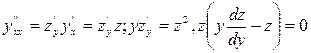 .
.
Приравниваем к нулю каждый из сомножителей левой части:
a) z = 0, y’ = 0, y = C;
б) 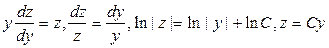 ,
,
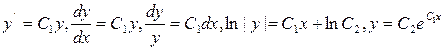 .
.
Ответ: y = C2eC/x.
2) Найти решение уравнения у"+y = ctgx, удовлетворяющее условиям 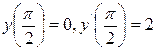 .
.
Решение. Рассмотрим соответствующее однородное уравнение у"+у = 0, его характеристическое уравнение х2 + 1 = 0, откуда x1,2 = ±i и общее решение однородного уравнения будет у = С1sinx + С2cosч. Далее по методу Лагранжа решение неоднородного уравнения в виде у = φ1(x)sinx + φ2(x)cosx, причем функции φ1(x) и φ2(x) определяются из системы
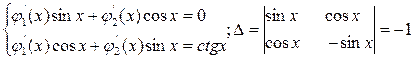 ;
;
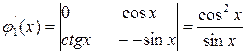 ;
;
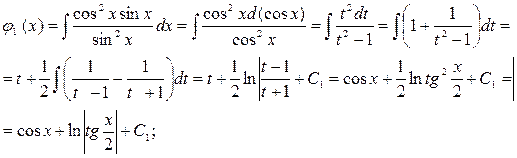
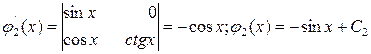 .
.
Итак, общее решение неоднородного уравнения имеет вид
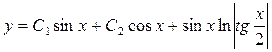 .
.
Удовлетворим начальным условиям:
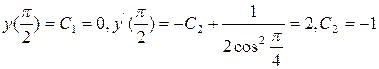 .
.
Ответ: 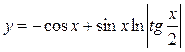 .
.
10. Решить систему 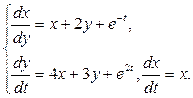
Решение. Методом исключения получаем х - 4х - 5х = -4е-t + 2e2t,
при этом 2у = 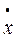 – х – е-t. Соответствующее однородное
– х – е-t. Соответствующее однородное 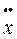 - 4
- 4 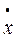 - 5х = 0 имеет решение
- 5х = 0 имеет решение
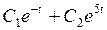 .
.
Частное решение неоднородного следует искать в виде xz = Atе-t + Bе2t (-1 - корень характеристического уравнения). Дифференцируя 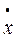 z = -Atе-t + Aе-t + 2Bе2t,
z = -Atе-t + Aе-t + 2Bе2t, 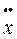 z = Atе-t - 2Aе-t + 4Bе2t, и подставляя в уравнение, получим
z = Atе-t - 2Aе-t + 4Bе2t, и подставляя в уравнение, получим
-6Aе-t – 9Bе2t = -4е-t + 2е2t,
следовательно, A = 2/3, B = -2/9, xz = 2/3tе-t – 2/9е2t.
Тогда
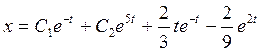 .
.
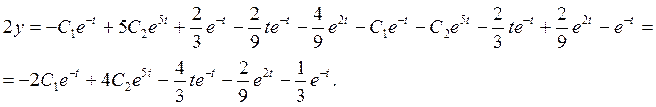
Ответ: 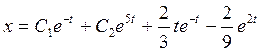 ,
,
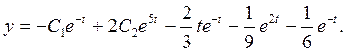
 Раздел 6. Кратные интегралы. Элементы теории векторного поля
Раздел 6. Кратные интегралы. Элементы теории векторного поля
|
|
|
|
|
Дата добавления: 2014-11-20; Просмотров: 548; Нарушение авторских прав?; Мы поможем в написании вашей работы!