Вычисление двойного интеграла. Изменение порядка интегрирования

Свойства двойного интеграла

Литература: [5, гл. 2, §2.3; 6: гл. 1, § 2].

Свойства двойного интеграла аналогичны свойствам определённого интеграла. Приведем их без доказательства.

1. Двойной интеграл от суммы конечного числа функций равен сумме
двойных интегралов от слагаемых функций:

. (6.2.3)

2. . (6.2.4)

3. Если область интегрирования D разбить на n частей D_k, то

(6.2.5)

4. Если (x,y)єD, f(x,y) ≥ g(x,y), то

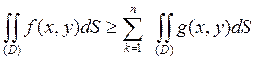. (6.2.6)

5. Теоремы об оценке двойного интеграла.

Если (х,у)єD, m≤f(x,y)≤M (m - наименьшее, М- наибольшее значе­ния функции в области), то

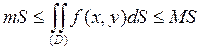. (6.2.7)

где S - площадь области D.

6. В области D существует такая точка N(х₀,у₀), что

. (6.2.8)

Значение функции z - f(x,y) называется средним значением функции в об­ласти D.

7. 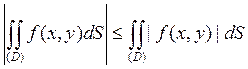(6.2.9)

Литература: [3; №№ 3485 - 3504, 3506 - 3516; 5; гл. 2, §§ 2.4 - 2.5; 6; гл.1, §5].

Для вычисления двойного интеграла в декартовой системе координат найдём дифференциал элемента площади dS. Так как двойной интеграл не зависит от способа разбиения области D*, то разобьем ее линиями x_i = const и y_i = const на прямоугольные ячейки D*_i со сторонами ∆x_i и ∆y_i. Тогда ∆S_i = ∆х_i ∆y_i в пределе при max(diamD_i) —> 0 получим ds = dxdy.

Таким образом,

. (6.2.10)

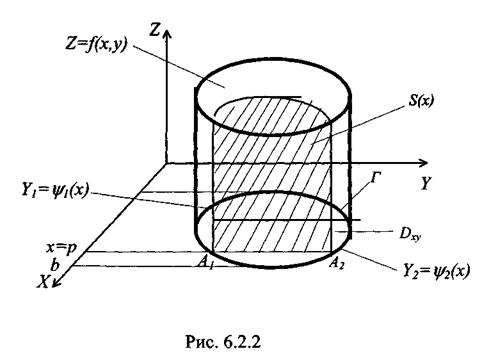
Пусть интеграл (6.2.10) выражает объём V цилиндрического тела с ос­нованием D ограниченного поверхностью z = f(x,y). Проведём линии х=а, х=b, проходящие через крайние точки границы Г правильной области D (см. рис. 6.1.1).

Точками А и В граница Г делится на два участка AЕВ и АСВ. Пусть уравнения этих линий АСВ: у = ψ₁(х), АЕВ: у = ψ₂(х). Проведём линию х = р = const через внутреннюю точку М области D. Первая линия у = ψ₁(х), кото­рую пересекает прямая х-р в направлении Оу, называется "входящей" лини­ей области D, вторая - у = ψ₂(х) - "выходящей".

Аналогично предыдущему проведём линии у - с, у = d, касающиеся границе области Г в точках Си Е, которые разбивают границу на линии САЕ и СВЕ (см. рис. 6.1.1). Обозначим их уравнениях x = φ₁(y) и х = φ₂(у) соответ­ственно.

Известно, что объём тела можно вычислить с помощью определённого интеграла методом параллельных сечений:

, (6.2.11)

где S (х) - площадь поперечного сечения в плоскости х - р = const (рис. 6.2.2). В свою очередь, площадь S(x) найдем также посредством определен­ного интеграла:

. (6.2.12)

Тогда, подставляя выражение (6.2.12) в (6.2.11), получаем

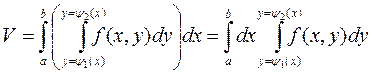. (6.2.13)

Если провести сечение y=h=const, то для вычисления двойного инте­грала будем иметь другую формулу:

. (6.2.14)

Выражения (6.2.13) и (6.2.14) представляют собой повторные (или двукратные) интегралы. Интегралы и называются внутренними, а интегралы , 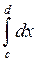- внешними.

Итак, двойные интегралы вычисляются путём сведения их к двукрат­ным. Нижний и верхний пределы интегрирования внутренних интегралов в (6.2.13), (6.2.14) - это уравнения "входящих" и "выходящих" линий, ограни­чивающих область D. В каждом конкретном случае, в зависимости от вида области D или подынтегральной функции, выбираем одну из формул:

. (6.2.15)

. (6.2.15)

а переход от (6.2.15) к (6.2.16) или наоборот называется заменой порядка ин­тегрирования.

Замечание 1. Если область D не является правильной, то двойной ин­теграл нельзя представить в виде двукратного. Тогда разбивают область D на ряд правильных областей и пользуются свойством 3 (см. п. 6.2.2).

Замечание 2. При вычислении внутреннего интеграла в выражении (6.2.13) величина у - переменная, а х считается постоянной, у внутреннего интеграла (6.2.14) - наоборот: х - переменная, у = const.

Замечание 3. Формулы вычисления двойного интеграла (6.2.15), (6.2.16) упрощаются, если область D слева и справа (или сверху и снизу для выражения (6.2.16)) ограничена отрезками прямых линий так, что линии х = а, х - b (или у = с, у = d для выражения (6.2.16)) совпадают с этими участка­ми границы (например, рис. 6.2.3 - 6.2.5).

Замечание 4. Если уравнения "входящей" и "выходящей" линий у = ψ₁(х), у = ψ₂(х) заданы на интервале [а,b] различными аналитическими вы­ражениями, то область интегрирования D надо разбить на несколько облас­тей D_k так, чтобы для каждой области уравнения "входящей" и "выходящей" линий задавались одним аналитическим выражением.

Пример 6.2.1. Расставить пределы интегрирования по области D и вы-числить двойной интеграл: D: {х≥0, у = х, у = 2-х²}, f(x,y) = х + у.

Решение. Область является правильной (см. рис. 6.2.3). Внешний инте­грал вычислим по х. Находя точки пересечения линий у = х и у = 2 - х² (х₁=0; х₂=^:1), проведём линии через крайние точки области. Внутренний интеграл вычислим по y. "Входящая" линия -yj= х, "выходящая" - у₂ = 2- х²:

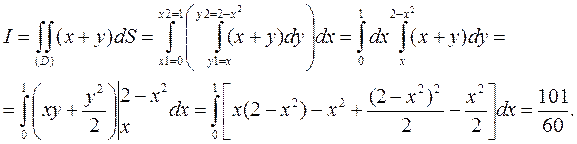
Изменим порядок интегрирования. Внешний интеграл вычислим по у (проводим линии у₁ = 0; у₂ = 2 (рис. 6.2.4)).

Заметим, что уравнение "входящей" линии (вдоль OY) - это линия x₁ = 0, а "выходящая" - состоит из двух линий: у-х и у = 2-х². Разобьем область (D) линией у = 1 на области D₁ и D₂ так, чтобы в каждой из них вы­ходящая линия выражалась одним уравнением: (см. рис. 6.2.4). По свойству интеграла (6.2.3) получим:

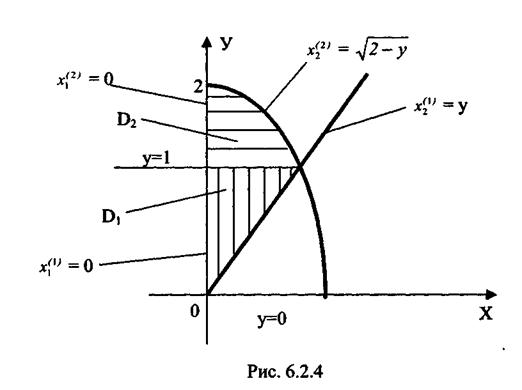= (сделаем замену переменных в последнем интеграле) =

.

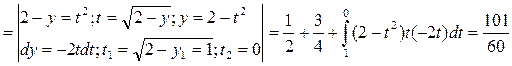Очевидно, что при изменении порядка интегрирования второй вариант слож­нее первого, так как приводит к вычислению двух интегралов.

Пример 6.2.2. Расставить пределы интегрирования по области D и из­менить порядок интегрирования. D: {х² + у² = 2ах; у² - 2ах; х = 2а; у ≥ 0}.

Решение. Заметим, что область является правильной лишь в направле­нии оси OY (рис. 6.2.5). Пусть сначала внешний интеграл будет вычисляться по х, а внутренний - по у. Проведём линии x₁ = 0, х₂ = 2а через крайние точки области. "Входящая" линия – 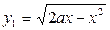, 'выходящая" - 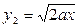. Тогда

.

Так как части круга и параболы, ограничивающие данную область, расположены в области у ≥ 0, то из уравнений у² = 2ах, х² + у² = 2ах => 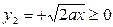, 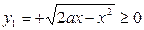. Эти функции являются пределами ин­тегрирования. Так как область D в направлении оси ОХ не является пра­вильной, разобьем её линией у = а на три правильные области: D₁, D₂, D₃ (см. рис. 6.2.5):

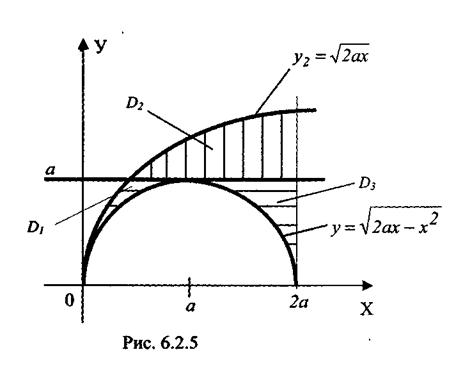
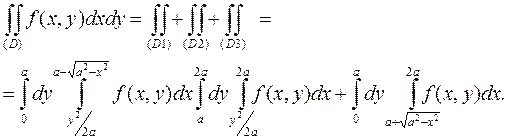
Здесь уравнения "входящих" линий для областей D₁, D₂, D₃: х⁽¹⁾₁ = х⁽²⁾₁ = у²/2а, а х⁽³⁾₁ найдём из уравнения окружности . Уравнения "выходящих" линий: 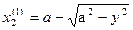(из уравнения окружно­сти), .

Дата добавления: 2014-11-20