Замена переменных в тройных интегралах

Литература: [3, №№3552 – 3558, 3609 - 3625; 5, гл. 2, §§ 2.6 – 2.10; 6, гл.2, §4].

Проводя рассуждения о замене переменных, аналогичные случаю с двойным интегралом (см. подразд. 6.2.4), и рассматривая однозначное отображение ограниченной области V пространства OXYZ на область V^* пространства 0uvw с помощью непрерывно дифференцируемых функций x = x(u,v,w), y = y(u,v,w), z = z(u,v,w), можно доказать, что такому отображению соответствует функциональный определитель (якобиан преобразования)

.

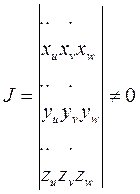Справедлива формула

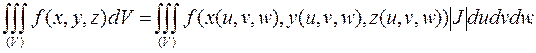
Цилиндрическая система координат. Положение точки в пространстве однозначно определяется заданием трех величин ρ, φ, z (рис. 6.3.4).

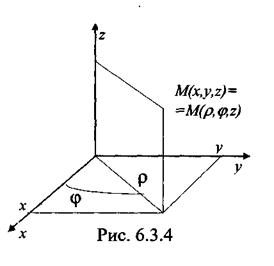Очевидна связь декартовой и цилиндрической системы координат:

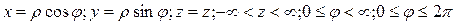(6.3.5).

Две первые формулы дают на плоскости OXZ связь декартовых и полярных координат.

Якобиан преобразования в тройном интеграле при замене по формуле (6.3.5) равен

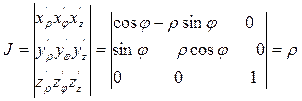
Тогда

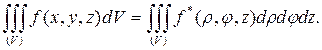(6.3.6)

С другой стороны, так как тройной интеграл не зависит от способа разбиения области V на элементы ∆V_i, то разобьем ее на элементы координатными поверхностями цилиндрических координат:

ρ = const - цилиндры радиуса ρ;

φ = const - плоскости, проходящие через ось 0z;

z = const - горизонтальные плоскости.

Эти поверхности разбивают область V на элементы ∆V_i. Объем элемента объема равен произведению площади основания dS на высоту dz: ∆V=dSdz=ρdρdφdz.

Пределы интегрирования в цилиндрических координатах расставляются аналогично декартовым, но не плоскости OXY вводятся полярные координаты:

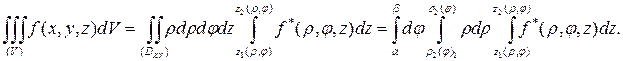
Здесь f^*(ρ,φ,z) = f(ρcosφ,ρsinφ,z).

Сферические координаты. Положение точки М(x,y,z) в пространстве однозначно определяется заданием трех величин r, φ, θ. Направление отсчета переменных r, φ, θ указано на рис. 6.3.5: 0≤r<∞; 0≤φ≤2π; 0≤θ≤π. Очевидна связь декартовой и сферической систем координат: x = rsinθcosφ; y = rsinθsinφ; z = rcosθ. (6.3.7)

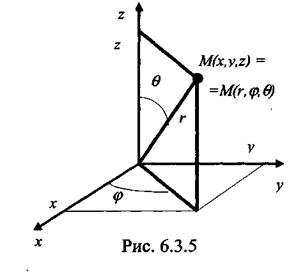Координатные поверхности сферических координат: r = const - сферы, θ = const - конусы, φ = const - плоскости. Якобиан преобразования

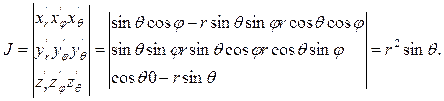
Тогда

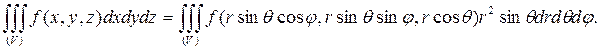(6.3.8)

Таким образом, чтобы вычислить тройной интеграл в сферических координатах, необходимо выполнить замену переменных по формулам (6.3.7) и перейти к повторному интегрированию по переменным r, φ, θ. Переход к сферическим координатам особенно удобен при интегрировании по объемам, ограниченным сферически-коническими поверхностями.

Для вычисления объемов тел в цилиндрической и сферической системе координат используются формулы (6.3.6-6.3.8) с f(x,y,z) ≡ 1.

Пример 6.3.3. Вычислить 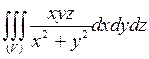, где область интегрирования ограничена поверхностью .

Решение. Представим в сферических координатах уравнение границы объема: так как x² +y² +z² = r, то S: (r²)² = a²r²sin²θcosφsinφ. Поэтому

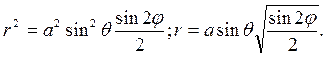
Для подынтегральной функции

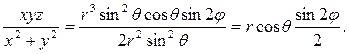
Объем расположен симметрично координатной плоскости OXY в I, V и III, VII октантах, причем в каждой из симметричных частей объема 0≤φ≤π/2; 0≤θ≤π/2:

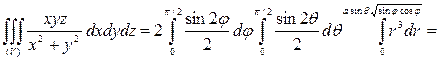
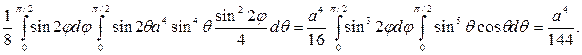
Дата добавления: 2014-11-20