И физический смысл

Определение двойного интеграла, его геометрический

Тема 6.2. Двойной интеграл

Тема 6.1. Некоторые вспомогательные определения

Рассмотрим множество D точек плоскости (или пространства).

Если присоединим к области D все её граничные точки, то получим замкнутую область D*. Область D* называется ограниченной, если ее можно поместить внутрь некоторого круга (сферы) конечного радиуса R.

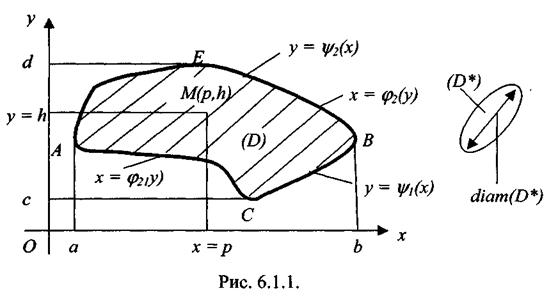
Пусть имеем в плоскости OXY замкнутую область D*. Проведём через произвольную внутреннюю точку М(х, у) є D прямую, параллельную оси OY (или ОХ). Если эта линия пересечёт границу области Г только в двух точках, то область называется правильной в направлении оси OY (ОХ). Область D*, правильная вдоль оси ОХ и OY, будет просто правильной областью. Диаметр области D*: diam(D*) - это наибольшее расстояние между двумя точками её границы (рис. 6.1.1). Выражение [z = f(x,y) є C(D*)] обозначает, что в об­ласти D* непрерывны как функция z =f(x,y), так и её производные до поряд­ка n включительно.

Литература: [3; №№ 3460 - 3476, 3477 - 3484; 5; гл. 2, §§ 2.1 - 2.2; 6; гл. 1, §§1-2].

Рассмотрим в плоскости OXYзамкнутую конечную область D* = D 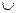Г площади S, где Г - её граница. Пусть функция Z=f(x,y) определена и непре­рывна в D*. Разобьем область D* сетью линий на конечное число областей, площади которых ∆S_i (i=l,..., n). В каждой области выберем точку М_i (х_i, у_і) є D_i (рис.6.2.1). Найдём значения функции f(M_i) и составим сумму

(6.2.1)

называемую интегральной суммой для функции z=f(x,y) в области D.

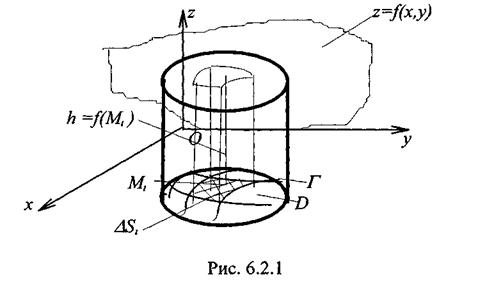
Если f(x,y) > 0 для (х,у)єD то каждое слагаемое [f(M_k) ∆S_k] пред­ставляет собой объём ∆V_i малого цилиндра с площадью основания ∆S_i и вы­сотой h_i =f(M_i) (см. рис. 6.2.1). Сумма объёмов ∆V_i (6.2.1) при этом определя­ет объём ступенчатого тела, сложенного из малых цилиндров.

Очевидно, что область D можно по-разному разбить сетью линий на площадки ∆S_i. Тогда интегральные суммы в выражении (6.2.1) при каждом разбиении будут отличаться друг от друга, а в совокупности они образуют последовательность интегральных сумм

V_n1, V_n2, V_n3, …, V_nk.

Чем больше число разбиений щ, тем меньше объём ступенчатой фигу­ры отличается от объёма цилиндрического тела, ограниченного поверхно­стью z = f(x,y), плоскостью OXZ, цилиндром с образующей, параллельной оси OZ, и направляющей - границей Г области D (см. рис. 6.2.1).

Увеличим число разбиений n →∞, причём max(diamD*)→0.

Справедлива следующая теорема.

Если функция f(x,у)єC*(D), to lim V_nk (к = 1,2...) (предел последовательности интегральных сумм) при max(diamD*)→0. Этот предел не зави­сит ни от способа разбиения области Д ни от выбора точки М_iє∆S_i. Он на­зывается двойным интегралом от функции f(x,y) по области D и обозначается

, (6.2.2)

max(diamD*)→0, где f(x,y) - подынтегральная функция; dS – дифференциал элемента площади области интегрирования D.

Геометрический смысл двойного интеграла состоит в том, что он чис­ленно равен объёму цилиндрического тела (см. рис. 6.2.1).

Физический смысл двойного интеграла - интеграл от функции z=f(x.y) > 0 по области D представляет собой массу пластинки D, если f(х,у) -плотность её в точке М.

Дата добавления: 2014-11-20