Указания. Тема 5.2. Уравнения высших порядков

Тема 5.2. Уравнения высших порядков

Вопросы для самопроверки

1. Сформулируйте теорему существования и единственности решения диф­ференциального уравнения первого порядка.

2. Приведите пример однородного дифференциального уравнения первого порядка и его решение.

3. В чем состоит метод вариации произвольной постоянной при решении линейного уравнения первого порядка? Приведите пример.

4. Как и в каких случаях интегрируются в квадратурах уравнения, не разре­шенные относительно производной?

Учебники: [16, гл. 15, §§ 3 - 5], [22, гл. 11, §§ 1 - 3, 5, 6], [17, гл. 13, §§21-25].

Аудиторная работа. Решить примеры: [20, гл. 9, § 2, №№ 9.212, 9.216, 9.247, 9.249, 9.331, 9.338, 9.360, 9.374], [15, гл. 12, §§ 7 - 10, №№ 2164, 2167, 2186, 2194, 2221, 2246], [30, задание 2, 2.1: №№ 1, 14].

Самостоятельная работа: [20, гл. 9, § 2, №№ 9.211, 9.219, 9.221, 9.248, 9.249, 9.323 - 9.330, 9.337, 9.339, 9.354 - 9.357, 9.370, 9.373], [15, гл. 12, §§ 7 -10, №№ 2163, 2165 - 2170, 2185 - 2192, 2213 - 2219, 2247], [30, задание 2, 2.1: №№2, 5, 12].

Студент должен владеть методами решения дифференциальных урав­нений первого порядка, интегрируемых в квадратурах: с разделяющимися переменными, однородных и линейных. К ним обычно будут сводиться уравнения высших порядков, допускающие понижение порядка.

Дифференциальное уравнение n -го порядка имеет вид

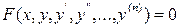или .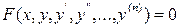

Задачей Коши для такого уравнения называется задача отыскания ре­шения у(х), удовлетворяющего заданным начальным условиям:

Общим решением называется такая функция у = φ(х, С₁,..., С_n), кото­рая при любых допустимых значениях параметров С₁,..., С_n является реше­нием дифференциального уравнения, и для любой задачи Коши найдутся по­стоянные С₁,..., С_n, определяемые из системы

φ(х₀, С₁,..., С_n) = y₀,

φ^’(х₀, С₁,..., С_n) = y^’₀,

Уравнение Ф(х,у,С₁,...,С_n) = 0, определяющее общее решение как не­явную функцию, называется общим интегралом дифференциального уравне­ния.

В качестве примеров рассмотрим уравнение четвертого порядка 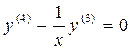, которое допускает понижение порядка заменой р=у³, получаем (переменные разделились), р = С₁х.

Возвращаемся к исходной функции у: у" = С₁х, интегрированием найдем общее решение .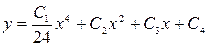

Линейным неоднородным уравнением n -го порядка называется урав­нение вида у⁽ⁿ⁾ +а₁(х)у^(n-1) +... + а_n(х)у = f(x), в котором f(х)≠0. Общее решение этого уравнения определяется формулой y(x) = y₀₀(x)+y_ZH(x), где y_оо(x) - общее решение соответствующего однородного уравнения, а y_ZH(x) - некоторое частное решение неоднородного [16, гл. 15, § 4].

Линейные уравнения с постоянными коэффициентами составляют важнейший класс уравнений, интегрирование которых сравнительно легко доводится до конца.

Пример 5.2.1. у"-5у^’ +6у = х + 1.

Решение. Рассмотрим соответствующее однородное уравнение у"-5у'+6у = 0. Подстановка Эйлера у = е^λx приводит к характеристиче­скому уравнению λ² - 5λ + 6 = 0, его корни λ₁ = 2, λ₂ = 3, а общее решение y_оо= c₁e^2x + c₂e^3x. Частное решение неоднородного уравнения ищем в виде Ах + В, где коэффициенты А и В определяются подстановкой в исходное уравнение, получаем -5А + 6(А + В) = х +1, откуда 6А = 1, 6В - 5А = 1, т. е. A = 1/6, B = 11/36. Таким образом, общее решение исходного неоднородного уравнения y_оо= C₁e^2x + C₂e^3x + x/6 + 11/36.

Подобрать частное решение неоднородного уравнения можно в том случае, когда правая часть есть функция специального вида [16, гл. 15, § 5J. Поэтому большое значение имеет метод вариации постоянных, дающий воз­можность проинтегрировать неоднородное линейное уравнение, если извест­но общее решение соответствующего однородного уравнения [16, гл. 15, § 4].

Дата добавления: 2014-11-20