Указания

Тема 5.3. Системы дифференциальных уравнений

Вопросы для самопроверки

1. Сформулируйте теорему существования и единственности дифференци­ального уравнения n -го порядка.

2. Какие уравнения высших порядков допускают понижение?

3. В чем состоит метод вариации постоянных для линейного уравнения вто­рого порядка? Привести пример.

4. Как ищут частные решения неоднородного уравнения, если его правая

часть имеет следующий вид: а) е^2х; б) sin л/Ух; в) х²?

Учебники: [16, гл. 15, § 6], [22, гл. 3, §§ 1 - 5], [17, гл. 13, §§ 29, 30].

Аудиторная работа: [20, гл. 9, § 3, №№ 9.432, 9.437, 9.442], [15, гл. 12, § 12; Ms 2276, 2279], [30, задание 5, п. 5.1: № 11; п. 5.2: № 6].

Самостоятельная работа: [20, гл. 9, § 3, №№ 9.431, 9.433, 9.438, 9.441, 9.443], [15, гл. 12, § 12, Ms 2275, 2277, 2228], [30, задание 5, п. 5.1: №№ 1 -4,12; п. 5.2: №№1-3, 7].

Система дифференциальных уравнений первого порядка имеет вид

у^'₁(x) = f(х, y₁,..., y_n)

у^'₂(x) = f₂(х, y₁,..., y_n)

…………..

у^'_n(x) = f_n(х, y₁,..., y_n)

Решением системы на интервале а<х<b называется совокупность функций y_i =φ_i(x)(i=l,...,n), непрерывно дифференцируемых на (a,b) и об­ращающих уравнения системы в тождества относительно xє(a,b).

Дифференциальное уравнение n-го порядка у⁽ⁿ⁾ = f(x, y, y',...,y^(n-1)) можно свести к системе уравнений первого порядка. И, наоборот, систему в большинстве случаев можно свести к уравнению n-го порядка, решая кото­рое можно найти и решение системы.

Пример 5.3.1.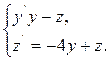

Решение. Возьмем из первого уравнения z = y - y', Отсюда z' = y' - y". Подставив эти выражения во второе, получим у' - у'' = -4у + у- у', или у" -2у' -3у = 0, общим решением этого уравне­ния будет у(х)= С₁е^-х + С₂е^3x.

Отсюда, используя Z = у - у' = C₁e^-x + С₂е^3х + С₁е^-x - 3С₂е^3х, полу­чим Z = 2C₁e^-x - 2С₂е^3х.

Ответ: y = C₁e^-x + С₂е^3х.

Z = 2(C₁e^-x - С₂е^3х).

Такой прием иногда называют методом исключения. Другим, встре­чающимся в приложениях, методом решения системы является нахождение интегрируемых комбинаций [22, гл. 3, § 3].

Дата добавления: 2014-11-20